什么是齐次方程? https://blog.csdn.net/shimly123456/article/details/136198159
行列式和是否有解的关系? https://blog.csdn.net/shimly123456/article/details/136198215
特征值和特征向量 参考视频:https://www.bilibili.com/video/BV1vY4y1J7gd/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
一个求特征值和特征向量 (手算,还包括矩阵相似对角化) 的例子:https://www.bilibili.com/video/BV14T4y127jf/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
一个更详细的求特征值和特征向量(手算,提到了“自由未知量”)例子:https://www.bilibili.com/video/BV1Js4y1372V/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
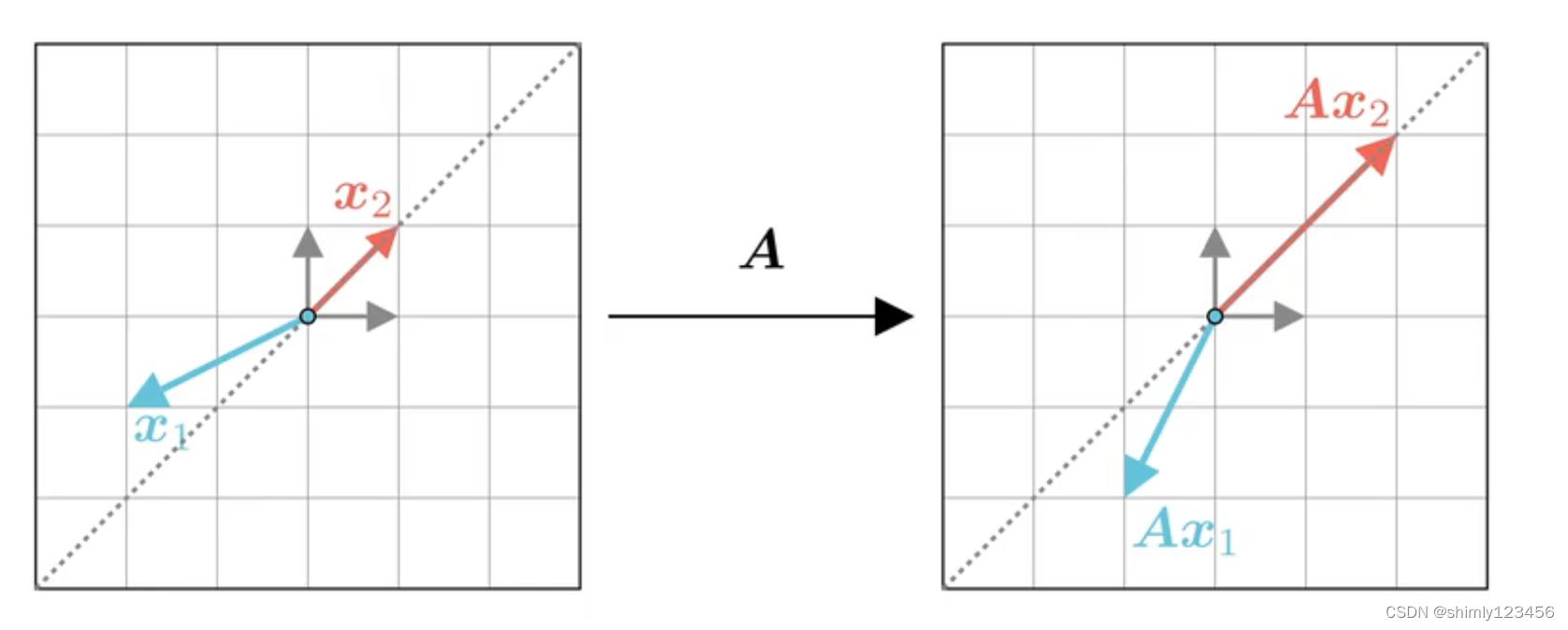
把矩阵 A 作为一个对向量的映射,x1 矢量在经过 A 映射后变换了方向,x2 经过 A 映射后保持原来的方式,只是长度发生了变化 (长度变换可以是负数,也就是 x2 方向变相反了也不影响)。像 x1 这种向量就不是 矩阵A 的特征向量;x2 这种向量就是矩阵 A 的特征向量
由于 矩阵A 对特征向量 x2 只起到了伸缩作用,那么就可以写下式子 (lamda 是一个常数、标量)
Ax2 = (lamda) * x2
在这里,(lamda) 就是特征值,x2 就是特征向量
所以,特征向量的严格定义就是:只要一个向量 x2 可以写成 Ax2 = (lamda) * x2。那么 lamda 就是矩阵 A 的特征值,x2 就是矩阵 A 的特征向量
一个矩阵可以有多个特征值和特征向量,如下图为例:
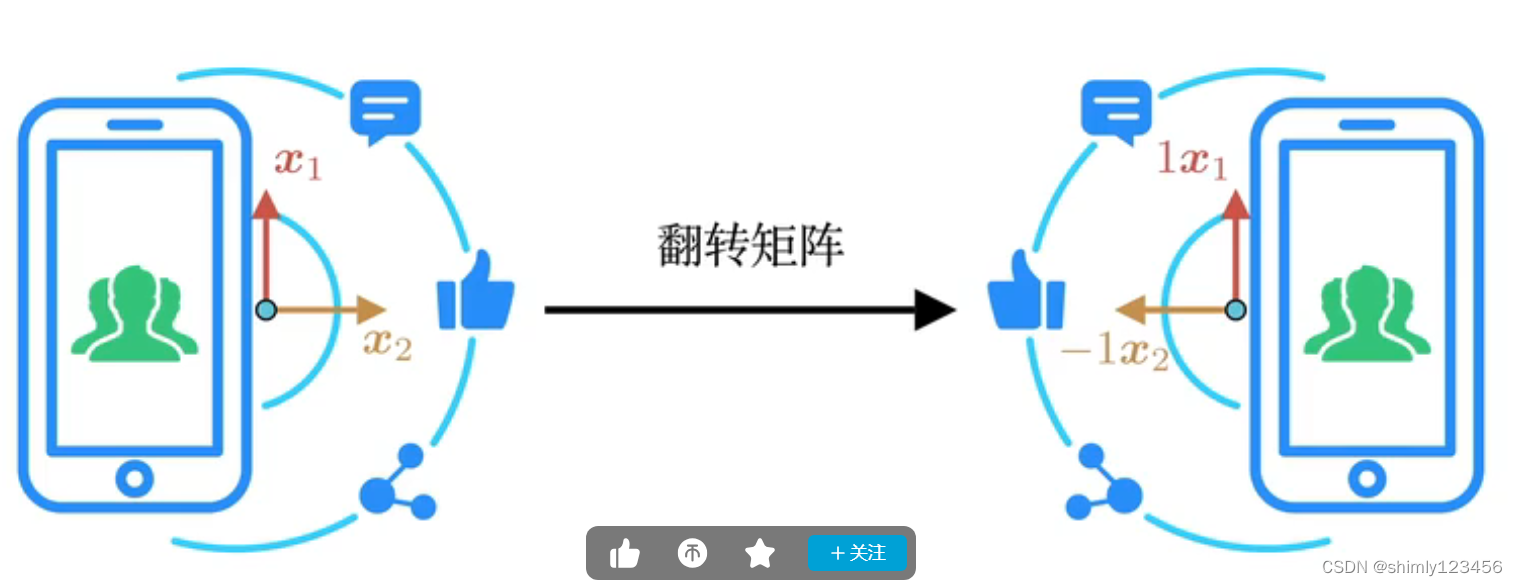
图片可以经过线性变化(或者说,矩阵乘法)进行翻转,只要把图片上的每一个像素点视为一个矢量,然后让它们乘以翻转矩阵即可。
在这里,经过翻转矩阵映射后,图片左右翻转了,每一个像素点(即,矢量) 在纵轴上的方向没有变化,所以有纵特征向量 x1,在横轴上的方向变反了,所以有横特征向量 x2。x1 和 x2 的特征值分别是 1 和 -1
接下来,我们看看特征值和特征向量的严格数学计算

如果看不懂,可以再看一遍参考视频,也就 6min,不长
以下是一个求特征值、特征向量,从而把矩阵相似对角化的例子:

当 lamda1 = lamda2 = 2 时,我们发现求出的矩阵只有一个非零行,那么也就是说它的 “自由未知量” 是 2。
这其实暗含了 “我们能够得到两个线性无关非零解” 的意思,也就说这个矩阵是可以相似对角化的