题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

我的想法：

        递归法

        万金油--层次遍历法

        当然上面两中都是笨方法，就算不是完全二叉树也能算，没有用到完全二叉树的特性。

我的代码：

        递归：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int count = 0;int countNodes(TreeNode* root) {int res = cont(root);std::cout << count<<endl;//cout数字也是正确的return res;}int cont(TreeNode* cur){if(cur == nullptr) return 0;count ++;return 1 + cont(cur->left) + cont(cur->right);}
};

层次遍历：

class Solution {
public:int countNodes(TreeNode* root) {if(root == nullptr) return 0;std::queue<TreeNode*> que;que.push(root);int count = 0;while(!que.empty()){TreeNode* node = que.front();que.pop();count++;if(node->left) que.push(node->left);if(node->right) que.push(node->right);}return count;}
};

利用完全二叉树特性：

思想：

        递归看这个分支是不是满二叉树，是：公式计算； 不是：单独计算

        

        完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

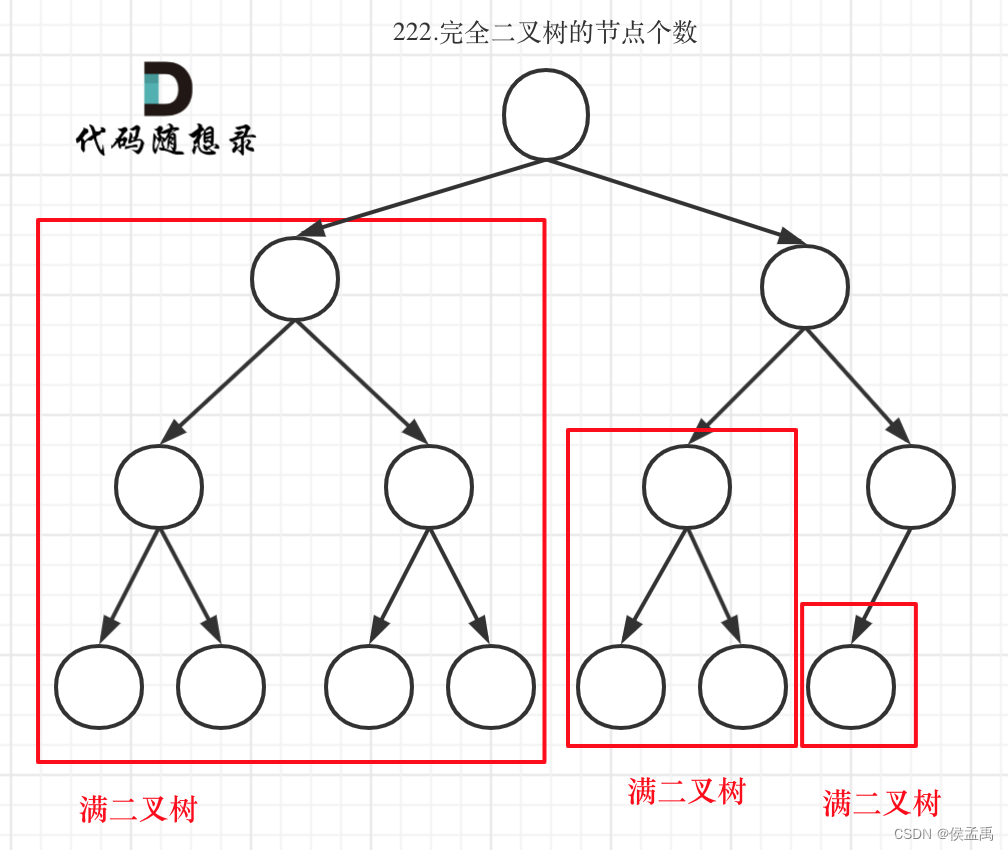
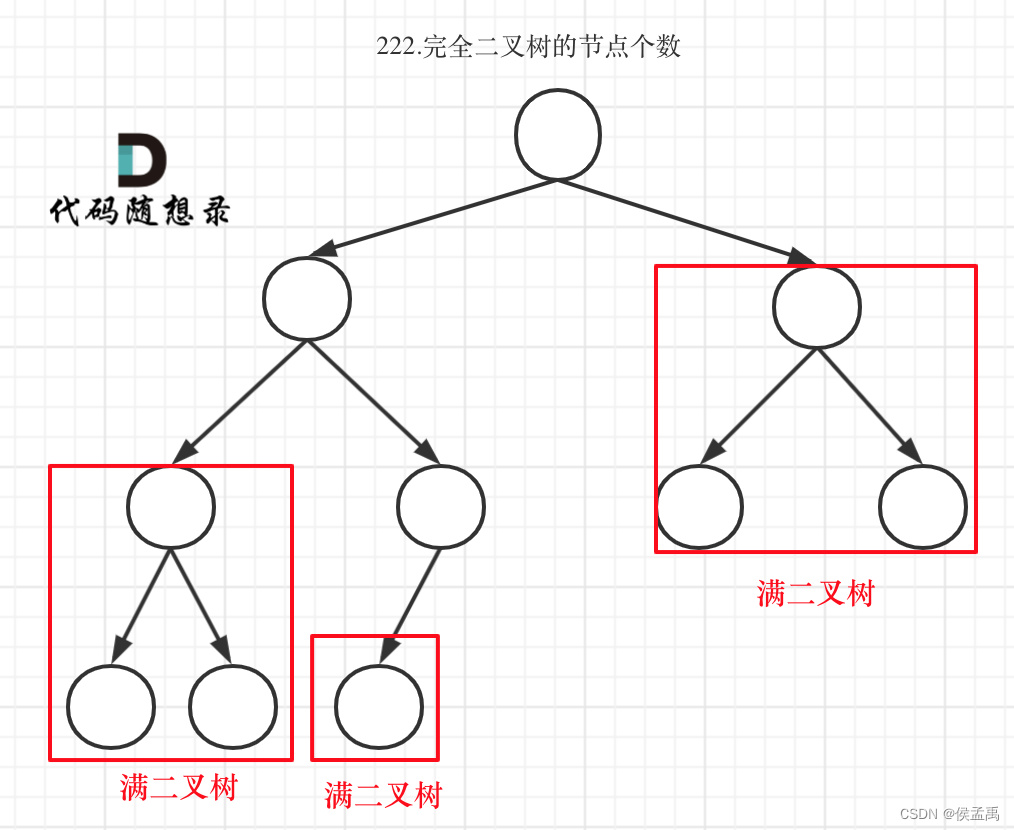
可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

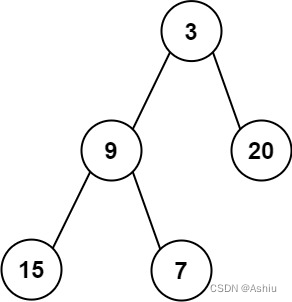
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：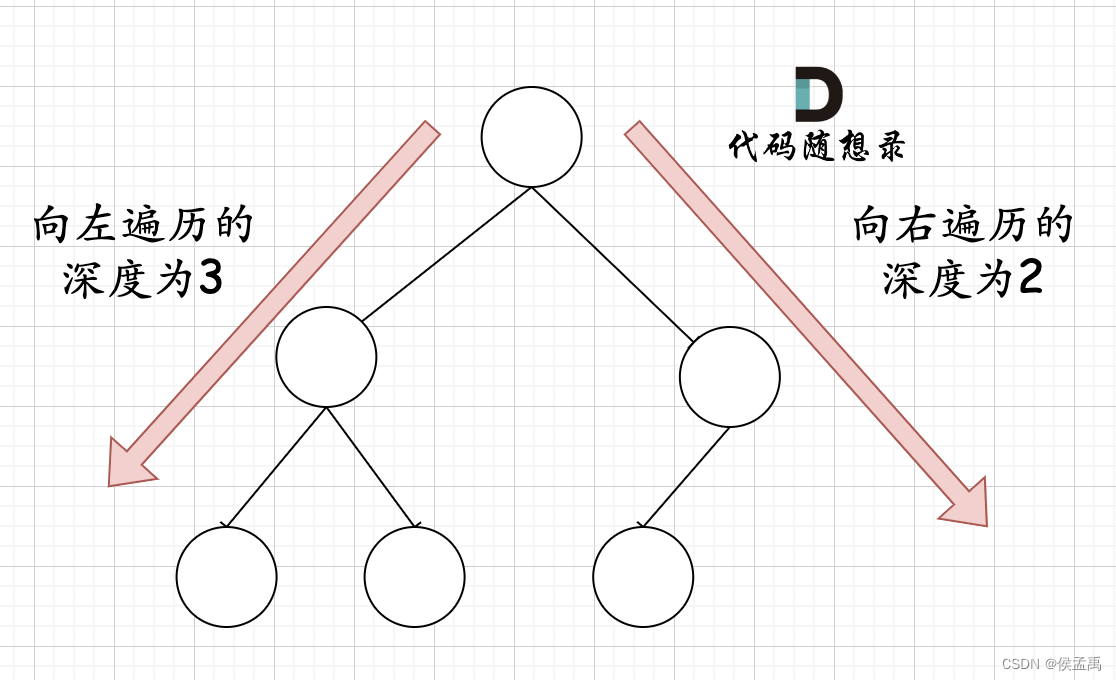 

class Solution {
public:int countNodes(TreeNode* root) {if (root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便while (left) {  // 求左子树深度left = left->left;leftDepth++;}while (right) { // 求右子树深度right = right->right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0}return countNodes(root->left) + countNodes(root->right) + 1;}
};