一，前言

为什么在这里要讲解红黑树？因为map与set的底层是红黑树，因此在这一节我们要讲红黑树的结构，之后会讲以红黑树为底层的map与set的封装。

二，红黑树的概念及其性质

什么是红黑树？
红黑树是一种平衡二叉树，其结点结构中多了表示颜色的成员变量（红或黑），红黑树通过结点间颜色匹配的限制，从而能够控制树的最长路径不会超过最短路径的2倍。

红黑树的性质：

每个结点不是黑色就是红色
根节点是黑色的
红节点的两个孩子都是黑色的
对于每个结点，从该结点到其所有后代叶结点的简单路径上，黑色结点数目相同
每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
为什么有了上述的几个条件就可以保证最长路径不超过最短路径的二倍呢？
由于规则三和规则四的限制，导致我们的最长路径一定是一红一黑结点搭配的；而最短结点则是全黑，且由于个规则四，黑色结点数目相同，因此最长路径就不会超过最短路径的二倍了。

红黑树的结点结构与AVL树的结点结构不同之处在于将AVL树结点中的平衡因子变量换为了表示颜色的变量。

enum Colour
{Red,Black
};template<class T>
struct TreeNode
{TreeNode<T>* _parent;TreeNode<T>* _left;TreeNode<T>* _right;Colour _col;T _data;TreeNode(const T& data):_parent(nullptr),_left(nullptr),_right(nullptr),_col(Red),_data(data){}};

并且，我们注意到红黑树新结点的默认颜色是红色？为什么要进行这样的设计呢？
通过观察红黑树的几条性质我们发现，当其默认结点颜色为黑色时，由于规则四，其新结点对这棵树一定会产生影响，而若新节点颜色为红色，则影响会比较小。
在这里插入图片描述

三，红黑树的插入

按照二叉搜索树的插入规则插入这部分我们在前面已经多次讲到，因此本节将不再讲解，最重要的还是其规则被破坏后，进行平衡的这一部分。
由于新插入结点的颜色默认为红色，若其双亲结点为黑色，则不违反任何规则，若其双亲结点为红色，则违反了规则三，需要进行调整。已经有人为我们总结几种调整的情况，我们只需要按照其总结进行调整就行。
几种需要调整的情况如下：

情况一：
当cur，p,u为红，g为黑时
调整方式：将p,u改为黑，g改为红。
若g为根节点，则需将根节点（g)改为黑色；
若不是，且g的双亲结点也为红色，则按此方式继续向上调整。直到调整完成或是到达根节点。（注：根节点都得调整为黑色）。

代码如下：

while (parent && parent->_col == Red){Node* grandparent = parent->_parent;assert(grandparent);assert(grandparent->_col == Black);if (grandparent->_left == parent){Node* uncle = grandparent->_right;//情况一if (uncle && uncle->_col == Red){parent->_col=uncle->_col = Black;grandparent->_col = Red;cur = grandparent;parent = grandparent->_parent;		else{Node* uncle = grandparent->_left;//情况一if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;grandparent->_col = Red;cur = grandparent;parent = grandparent->_parent;}		}}_root->_col = Black;return make_pair(_iterator(cur), true);}

情况二：

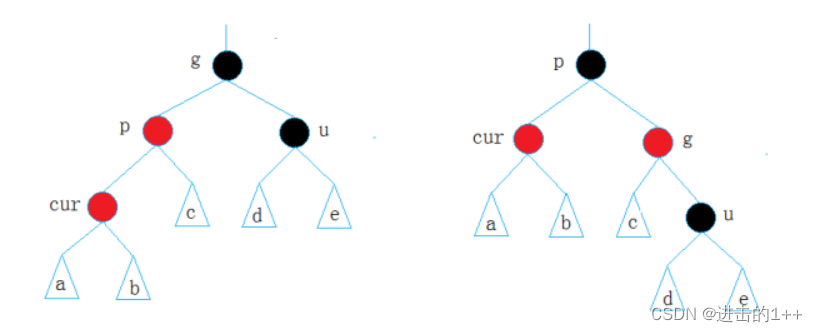
若cur,p为红，u为黑或者不存在时。

u的情况说明：
若u不存在，则cur一定是新插入的结点，若其不是新插入的结点，则p与cur一定有一个黑色结点，这不符合规则四。
若u存在，则cur一定不是新插入的结点，且原来为黑色，当新插入一个节点后调整为了红色。

若g的左子树为p,p的左子树为cur：调整方式，针对g做右单旋，并且将g改为红色，p改为黑色。
若g的右子树为p,p的右子树为cur：调整方式，针对做左单旋，并且将g改为红色，p改为黑色。
3. 情况三：
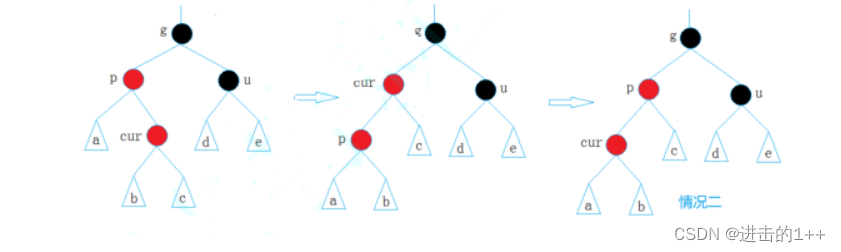
在这里插入图片描述
若g的左子树为p,p的右子树为cur，则先针对p做左旋，就和情况二相同了，再进行右旋。
若g的右子树为p,p的左子树为cur，则先针对p做右旋，就和情况二相同了，再进行左旋。

代码如下：

while (parent && parent->_col == Red){Node* grandparent = parent->_parent;assert(grandparent);assert(grandparent->_col == Black);if (grandparent->_left == parent){Node* uncle = grandparent->_right;//情况一if (uncle && uncle->_col == Red){parent->_col=uncle->_col = Black;grandparent->_col = Red;cur = grandparent;parent = grandparent->_parent;}else//情况二+三{if (parent->_left == cur){RotateR(grandparent);grandparent->_col = Red;parent->_col = Black;}else{RotateL(parent);RotateR(grandparent);grandparent->_col = Red;cur->_col = Black;}break;}}else{Node* uncle = grandparent->_left;//情况一if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;grandparent->_col = Red;cur = grandparent;parent = grandparent->_parent;}else//情况二+三{if (parent->_right == cur){RotateL(grandparent);grandparent->_col = Red;parent->_col = Black;}else{RotateR(parent);RotateL(grandparent);grandparent->_col = Red;cur->_col = Black;}break;}}}_root->_col = Black;return make_pair(_iterator(cur), true);}

四，红黑树的验证

我们通过验证红黑树的几条性质来验证这棵树是否为红黑树。

根节点为黑色结点
各路径的黑色结点数相同
红色结点的子节点为黑色
接下来，我们根据这几条规则来写代码判断是否为红黑树
代码如下：

bool Isbalance() {if (_root == nullptr){return true;}if (_root->_col == Red){cout << "根不是黑色结点" << endl;return false;}int BenchNum = 0;return PrevCheck(_root,0,BenchNum);}bool PrevCheck(Node* root, int BlackNum, int& BenchNum){if (root == nullptr){if (BenchNum == 0){BenchNum = BlackNum;return true;}else{if (BenchNum != BlackNum){cout << "路径黑色结点数量不同" << endl;return false;}elsereturn true;}}if (root->_col == Black){BlackNum++;}if (root->_col == Red && root->_parent->_col == Red){cout << "连续两个红色" << endl;return false;}return PrevCheck(root->_left, BlackNum, BenchNum) && PrevCheck(root->_right, BlackNum, BenchNum);}

五，map与set的封装

map与set的底层都是红黑树，那么如何用同一种底层结构去实现封装两个不同的数据结构呢？
事实上，在红黑树中其类模板为template<class K,class
T>。在map中T为pair<K,V>类型，在set中为K类型，这样就实现了同一底层封装两种不同的数据结构，也就是泛型编程。

红黑树迭代器的实现

红黑树是根据某种规则将一些结点链接起来的结构。因此其迭代器底层也与链表的迭代器一样，是结点指针，其重点是++和–的运算符重载。
通过观察，我们对++的重载有如下总结：平衡二叉搜索树按照中序遍历则是有序的。因此，对于++，则是找中序遍历的下一个结点。中序遍历的规则：左子树–根–右子树。
要找当前结点的下一个，则当其右子树不为空时，其右子树的最左边的结点就是下一个结点。
当右子树为空时，则向上找，直到cur!=parent->right，或parent为空其下一结点就为双亲结点。

代码如下：

Self& operator++(){if (_node->_right){Node* left = _node->_right;while (left->_left){left = left->_left;}_node = left;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_right == cur){cur = cur->_parent;parent = cur->_parent;}_node = parent;}return *this;}

–的重载与++相反，就不再详细讲解。
代码如下：

Self& operator--(){if (_node->_left){Node* right = _node->_left;while (right->_right){right = right->_right;}_node = right;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_left == cur){cur = cur->_parent;parent = cur->_parent;}_node = parent;}return *this;}

由于在插入时，map与set传入的类型不同，但都需要比较K类型对象，因此，我们在map与set中都写一个用于确定比较元素的类型的仿函数，map中由于T为pair<K,V>，(pair<K,V> kv)则需比较的是kv.first。
而set中的T为K，K key就直接比较key就行。

struct KeyOf{const K& operator() (const pair<K, V>& kv){return kv.first;}};struct KeyOfS{const K& operator()(const K& key){return key;}};

map重载[ ]

map的[ ]功能比较强大，它集查找，插入，修改功能为一体。

V& operator[](const K& key){pair<iterator, bool> ret = Insert(make_pair(key, V()));return ret.first->second;}

若树种有这个结点，则会插入失败，会返回这个结点的迭代器以及false。
在这里插入图片描述
由于重载函数返回的是V的引用，因此此结点的value便可以被修改。
若此结点不存在，则会插入一个V的匿名对象的value值。并返回其引用。

map的封装代码

以下是map的封装代码：

template<class K,class V>class map{struct KeyOf{const K& operator() (const pair<K, V>& kv){return kv.first;}};public:typedef  typename RBTree<K, pair<K, V>, KeyOf>::_iterator iterator;pair<iterator, bool> Insert(const pair<K, V>& kv){return _t.Insert(kv);}V& operator[](const K& key){pair<iterator, bool> ret = Insert(make_pair(key, V()));return ret.first->second;}iterator begin(){return _t.begin();}iterator end(){return _t.end();}private:RBTree<K,pair<K,V>, KeyOf> _t;};

set的封装代码

以下是set的封装代码：

template<class K>class set{struct KeyOfS{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, K, KeyOfS>::_iterator iterator;pair<iterator, bool> Insert(const K& key){return _t.Insert(key);}iterator begin(){return _t.begin();}iterator end(){return _t.end();}private:RBTree< K, K, KeyOfS> _t;};