目录
1 算法的评价
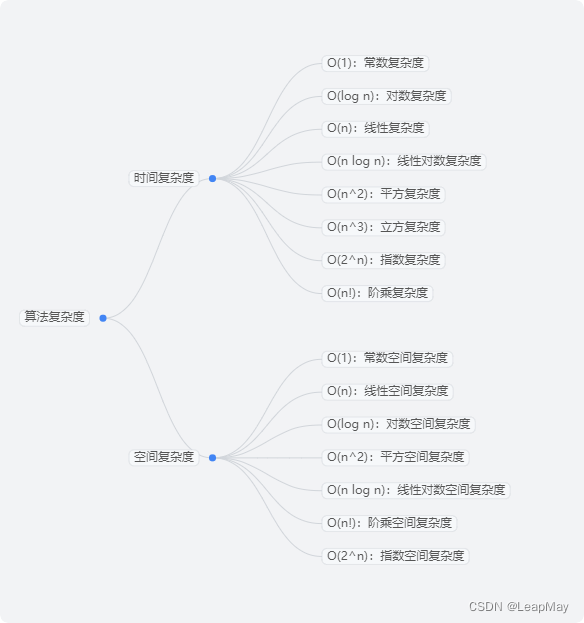
2 算法复杂度
2.1 时间复杂度(Time Complexity)
2.1.1 如何计算时间复杂度:
2.1.2 常见的时间复杂度类别与示例
2.2 空间复杂度
2.2.1 如何计算空间复杂度
2.2.2 常见的空间复杂度与示例
3 时间复杂度和空间复杂度计算示例
例子1:计算数组中所有元素的和。
例子2:快速排序算法。
例子3:递归实现斐波那契数列。
例子4:非递归实现的斐波那契数列。
例子5:二分查找算法。
例子6:冒泡排序算法。
1 算法的评价
评价算法的性能和效果是计算机科学和数据科学中的关键任务之一。如何评价算法的优劣可以从以下几方面展开:

时间复杂度和空间复杂度是算法性能分析的关键指标,它们用于衡量算法在处理不同规模输入时的时间和空间资源消耗。
2 算法复杂度
2.1 时间复杂度(Time Complexity)
时间复杂度是指在算法执行过程中,所需的时间资源与问题规模之间的关系。它主要衡量的是算法的执行效率,用于评估算法在不同规模数据下的操作时间。
时间复杂度通常使用大O符号表示,表示算法运行时间的增长率。
需要注意的是,时间复杂度只考虑算法的主要操作数量级,忽略了常数因子和低阶项。因此,两个时间复杂度相同的算法在实际执行中可能有着不同的执行效率。
2.1.1 如何计算时间复杂度:
- 分析每个操作的时间复杂度,包括循环、条件语句和函数调用。
- 计算每个操作的执行次数,通常是输入规模的函数。
- 合并所有操作的复杂度,通常选择最大的那个作为算法的时间复杂度。
时间复杂度的计算涉及以下几个方面:
基本操作次数: 时间复杂度的计算通常关注算法中执行的基本操作次数,例如赋值操作、比较操作、算术运算等。通常将这些操作的数量与输入规模相关联。
循环结构: 如果算法包含循环结构(例如for循环、while循环),需要考虑循环的迭代次数以及每次迭代中的基本操作数量。
递归调用: 对于递归算法,需要考虑递归的深度以及每次递归调用的时间复杂度。通常使用递归方程(递归关系式)来表示递归算法的时间复杂度。
分支结构: 如果算法包含分支结构(例如if语句),需要考虑每个分支的执行次数以及分支中的基本操作数量。
输入规模: 时间复杂度的计算通常与输入规模有关。输入规模表示算法操作的数据量或问题的大小,通常用符号n表示。
2.1.2 常见的时间复杂度类别与示例
常数时间复杂度(O(1)):无论问题规模多大,算法的执行时间都保持不变。例如,直接访问数组中的一个元素。
线性时间复杂度(O(n)):随着问题规模的增大,算法的执行时间也按线性比例增长。例如,遍历一个数组或链表中的所有元素。
对数时间复杂度(O(logn)):算法执行时间随着问题规模的增大而增长,但不是线性关系,而是以对数速率增长。例如,二分查找算法。
平方时间复杂度(O(n^2)):算法的执行时间与问题规模的平方成正比。例如,双重循环嵌套的算法。
指数时间复杂度(O(2^n)):算法的执行时间呈指数级增长,非常低效。例如,穷举法解决NP完全问题。
O(1) - 常数时间复杂度: 算法的执行时间是固定的,与输入规模无关。示例:
def constant_time_algorithm(arr):return arr[0]
O(log n) - 对数时间复杂度: 算法的执行时间随着输入规模的增加以对数方式增加。示例:
def binary_search(arr, target):low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return midelif arr[mid] < target:low = mid + 1else:high = mid - 1return -1
O(n) - 线性时间复杂度: 算法的执行时间与输入规模成正比。示例
def linear_search(arr, target):for i in range(len(arr)):if arr[i] == target:return ireturn -1
O(n^2) - 平方时间复杂度: 算法的执行时间与输入规模的平方成正比。示例:
def bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]
2.2 空间复杂度(Space Complexity)
空间复杂度是指算法在执行过程中所需的额外内存空间,它与问题规模之间的关系。空间复杂度用于评估算法的内存占用情况和资源消耗。
通常使用大O符号表示空间复杂度,表示算法所需的额外内存空间与问题规模之间的增长关系。
2.2.1 如何计算空间复杂度
- 分析算法的每个数据结构、变量和递归调用,以确定它们的空间占用。
- 计算每个数据结构和变量的空间占用,通常是常数项和与输入规模相关的项的和。
- 合并所有空间占用,通常选择最大的那个作为算法的空间复杂度。
空间复杂度的计算包括以下几个方面:
固定内存消耗: 指算法在运行过程中需要固定数量的内存空间,与输入规模无关。常见的固定内存消耗包括函数参数、常量变量、全局变量等。
额外数据结构: 如果算法使用了额外的数据结构来存储信息,如数组、列表、树、堆栈、队列等,需要考虑这些数据结构所占用的内存空间。通常需要考虑数据结构的大小和数量。
递归调用: 递归算法会使用栈空间来存储每一次递归调用的状态。递归的深度和每次递归调用的内存消耗会影响空间复杂度。
临时变量: 算法中使用的临时变量和计算过程中的中间结果也会占用内存空间。需要考虑这些变量的数量和大小。
输入数据的存储: 输入数据的存储也需要考虑在内。如果算法需要将整个输入数据存储在内存中,则空间复杂度与输入数据的大小成正比。
2.2.2 常见的空间复杂度与示例
常数空间复杂度(O(1)):算法所需的额外内存空间是一个常量值,不随问题规模的增大而改变。例如,只使用固定数量的变量或常量大小的数组。
线性空间复杂度(O(n)):算法所需的额外内存空间随问题规模的增大而线性增长。例如,需要根据输入构建一个同等大小的新数据结构。
平方空间复杂度(O(n^2)):算法所需的额外内存空间随问题规模的增大而平方级增长。例如,需要构建一个二维数组来存储所有可能的组合。
指数空间复杂度(O(2^n)):算法所需的额外内存空间随问题规模的增大而以指数级增长。例如,需要存储所有可能的子集或排列。
需要注意的是,空间复杂度只考虑算法本身所需的额外内存空间,不包括输入数据所占用的存储空间。另外,空间复杂度也可以根据最坏情况或平均情况来进行分析。
O(1) - 常数空间复杂度: 算法的内存使用与输入规模无关,占用固定的内存空间。示例:
def constant_space_algorithm(arr):result = 0for num in arr:result += numreturn result
O(n) - 线性空间复杂度: 算法的内存使用与输入规模成正比。示例:
def linear_space_algorithm(n):arr = [0] * nreturn arr
O(n^2) - 平方空间复杂度: 算法的内存使用与输入规模的平方成正比。示例:
def quadratic_space_algorithm(n):arr = [[0] * n for _ in range(n)]return arr
3 时间复杂度和空间复杂度计算示例
例子1:计算数组中所有元素的和。
def sum_array(arr):sum = 0for num in arr:sum += numreturn sum时间复杂度:O(n),其中n是数组中的元素数量。遍历数组需要依次访问每个元素一次,因此时间复杂度与数组的大小成线性关系。
空间复杂度:O(1)。算法只使用了一个额外的变量存储累加和,并没有占用随问题规模变化的额外内存。
例子2:快速排序算法。
def quicksort(arr, left, right):if left < right:pivot = partition(arr, left, right)quicksort(arr, left, pivot - 1)quicksort(arr, pivot + 1, right)def partition(arr, left, right):pivot = arr[right]i = left - 1for j in range(left, right):if arr[j] <= pivot:i += 1arr[i], arr[j] = arr[j], arr[i]arr[i + 1], arr[right] = arr[right], arr[i + 1]return i + 1时间复杂度:最好情况下为O(nlogn),最坏情况下为O(n^2)。快速排序平均情况下的划分操作需要O(n)的时间复杂度,且需要递归n次,因此总体复杂度为O(nlogn)。但在最坏情况下,划分不平衡导致某一边的规模接近n,此时的时间复杂度变为O(n^2)。
空间复杂度:最好情况下为O(logn),最坏情况下为O(n)。快速排序使用递归调用,每次递归调用都需要保存当前函数的堆栈信息,而在最坏情况下,可能需要递归n次,所以空间复杂度为O(n)。而在最好情况下,递归调用树的高度为logn,因此空间复杂度为O(logn)。
例子3:递归实现斐波那契数列。
def fibonacci(n):if n <= 0:return 0if n == 1:return 1return fibonacci(n - 1) + fibonacci(n - 2)时间复杂度:指数级别,为O(2^n)。由于递归调用会重复计算相同的斐波那契数,时间复杂度呈指数级增长。
空间复杂度:最好和最坏情况下均为O(n),取决于递归调用的最大深度n。每次递归调用都需要在堆栈中保存函数的局部变量和参数,因此空间复杂度为O(n)。
该代码实现了递归方式计算斐波那契数列的函数。
时间复杂度:指数级别,为 O(2^n)。每次递归调用都会产生两个新的递归调用,因此递归树的总节点数是指数级别的,递归树的深度是 n。所以,总体的时间复杂度是 O(2^n)。
空间复杂度:指数级别,为 O(n)。在递归调用过程中,需要使用栈来保存每次递归调用的参数和局部变量。由于递归树的深度是 n,所以空间复杂度是 O(n)。
需要注意的是,由于斐波那契数列的计算可以通过动态规划或迭代的方式进行优化,以降低时间复杂度和空间复杂度。递归方式计算斐波那契数列在面对较大的 n 值时,会导致非常高的时间和空间消耗。
例子4:非递归实现的斐波那契数列。
def fibonacci(n):if n <= 0:return 0a = 0b = 1for _ in range(2, n+1):c = a + ba = bb = creturn b这段代码实现了求解斐波那契数列的函数。
该代码的时间复杂度是 O(n),其中 n 是要计算的斐波那契数的索引。在 for 循环中,需要执行 n-1 次加法操作。因此,时间复杂度是线性级别的。
该代码的空间复杂度是 O(1),因为除了输入参数外,只使用了常数空间来存储变量 a、b 和 c。无论输入的 n 多大,空间占用都是固定的。
例子5:二分查找算法。
def binary_search(arr, target):low = 0 # 常数时间复杂度high = len(arr) - 1 # 常数时间复杂度while low <= high:mid = (low + high) // 2 # 常数时间复杂度if arr[mid] == target:return midelif arr[mid] < target:low = mid + 1else:high = mid - 1return -1
该算法的时间复杂度为O(logn),在二分查找算法中,每次迭代会将问题规模缩小一半,因此时间复杂度为对数级别。具体而言,时间复杂度是由二分查找的迭代次数决定的。
空间复杂度是 O(1),因为除了输入参数外,没有使用额外的数据结构或变量来存储数据。无论输入规模如何变化,空间占用都是固定的。
例子6:冒泡排序算法。
def bubble_sort(arr):n = len(arr)for i in range(n): # 线性时间复杂度for j in range(0, n-i-1): # 线性时间复杂度if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]时间复杂度是 O(n^2),其中 n 是数组 arr 的长度。冒泡排序算法的时间复杂度由两层嵌套循环决定。外层循环执行 n 次,内层循环从 0 到 n-i-1 遍历,其中 i 是外层循环的迭代次数。因此,总的比较次数是 n + (n-1) + (n-2) + ... + 2 + 1,即等差数列求和公式,可以简化为 (n^2 - n) / 2,近似为 n^2。因此,该代码的时间复杂度是 O(n^2)。
该代码的空间复杂度是 O(1),因为除了输入参数外,没有使用额外的数据结构或变量来存储数据。无论输入规模如何变化,空间占用都是固定的。
计算时间复杂度和空间复杂度通常需要分析算法的每个操作以及它们的频率和内存占用。最终,选择合适的数据结构和算法以及考虑性能优化策略都有助于确保算法在不同规模的问题上都能高效运行。