1、一维弦振动方程
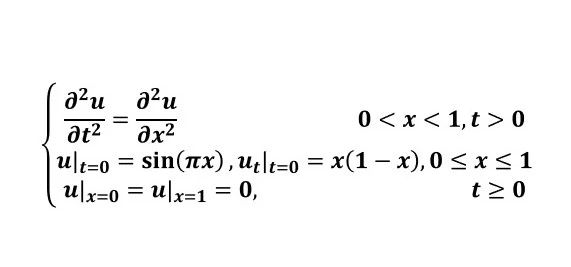
2、差分公式及求解
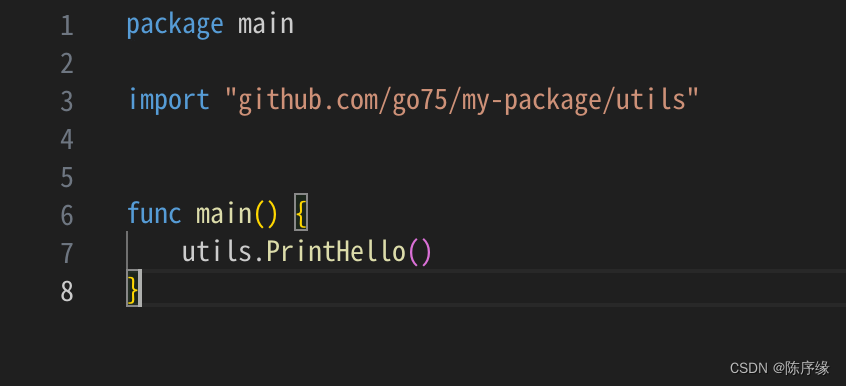
import numpy as np
import matplotlib.pyplot as plt
l=1 #长度
nx = 101 #x方向网格节点数量
dx = l/(nx-1) #空间网格步长
t=6 #总时间
dt = 0.01 # 时间步长
t_set=np.array([0.00,0.10,0.20,0.30,0.40,0.50,0.60]) #需要观察的时间
t_get=t_set/dt #需要观察的时间的步数# 指定初始条件
xp=np.linspace(0,l,num=nx)
u = np.sin(np.pi*xp)
utp=xp*(1-xp)*dt
u1=np.zeros(nx)
u1=u+utp
un1=u.copy()
un2=u1.copy()
# 计算
u_get=[] #需要观察的时间的波形
for n in range(int(t/dt)+1):if n in t_get.astype(int):if n==0:u_get.append(u)continueif n==1:u_get.append(u1)continueu_get.append(un2)un = np.zeros(nx)for i in range(1,nx-1):un[i] = dt**2/dx**2*(un2[i+1]+un2[i-1])+2*(1-dt**2/dx**2)*un2[i] - un1[i]un1=un2.copy()un2 = un.copy()fig = plt.figure()
plt.rcParams['xtick.direction'] = 'in' # 将x周的刻度线方向设置向内
plt.rcParams['ytick.direction'] = 'in' # 将y轴的刻度方向设置向内
clist = ['blue', 'red', 'green', 'black', 'darkgreen', 'lime', 'gold', 'purple', 'green', 'cyan', 'salmon', 'grey','mediumvioletred', 'darkkhaki', 'gray', 'darkcyan', 'violet', 'powderblue']
#绘制选的时间步的结果
for i in range(len(t_get)):plt.plot(xp, u_get[i], c=clist[i],lw =3,label= f't={t_set[i]}s')
plt.legend()
plt.show()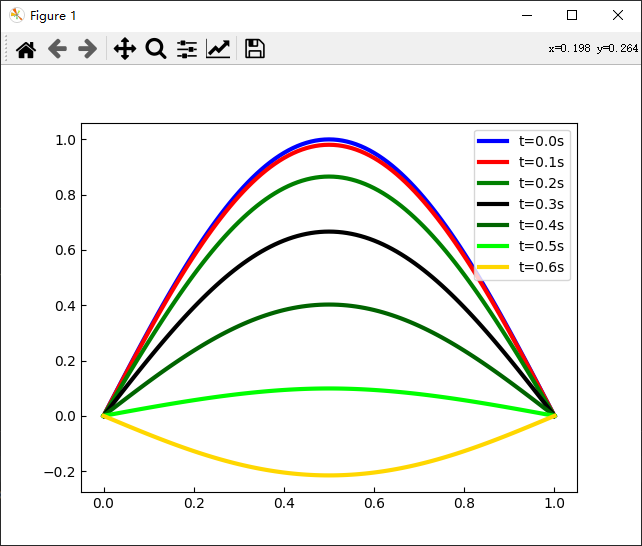
注意:时间不长和空间步长之比dt/dx<=1时,次解法是稳定且收敛的