大家好!今天我们来学习前缀和与差分算法。
目录
1. 一维前缀和
1.1 定义
1.2 计算方法
1.3 作用
1.4 适用场景
1.5 模板题
1.6 总结
2. 二维前缀和
2.1 定义
2.2 计算方法
2.3 模板题
2.4 总结
3. 一维差分
3.1 定义
3.2 差分数组
3.3 差分标记
3.4 作用
3.5 适用场景
3.6 模板题
4. 二维差分
4.1 定义
4.2 差分数组
4.3 差分标记
4.4 模板题
1. 一维前缀和
1.1 定义
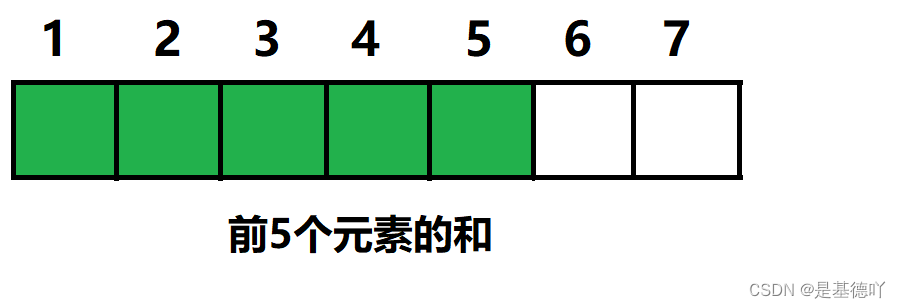
前缀和是一段序列里面前n项和。
例如,给定一个一维数组a,它的前缀和s[i]表示第1个元素到第i个元素的总和。也就是s[i]=a[1]+a[2]+a[3]+...+a[i-1]+a[i]
1.2 计算方法
s[i]=s[i-1]+a[i]
需要注意的是,数组的下标都是从1开始的!!!
1.3 作用
通过使用前缀和算法,可以在 O(1) 的时间复杂度内计算出任意区间的和,而不需要遍历整个区间。这对于多次查询区间和的场景非常有用,在处理一些数据范围较大的问题时非常高效。
1.4 适用场景
一个长度为n的数组a,m次询问,每次的询问区间是[l,r],求区间内所有数的和。
在没学过前缀和之前,对于求一段区间的和,我们的想法就是通过遍历这个区间的所有元素,直接暴力求解:
for (int i = l; i <= r; i++) {s += a[i];
} 这样直接遍历求和的做法时间复杂度是O(N)。如果再有m次询问,就需要两重循环求解,时间复杂度就为O(N*M),这样的时间复杂度非常高。
这时我们就可以用前缀和算法,通过O(1)的时间复杂度,直接求出某段区间的和。
具体做法:
首先做一个预处理,定义一个数组s,s[i]表示数组第1个元素到第i个元素的和。
求前缀和:
for (int i = 1; i <= n; i++) {s[i] = s[i - 1] + a[i];
}查询求区间和:
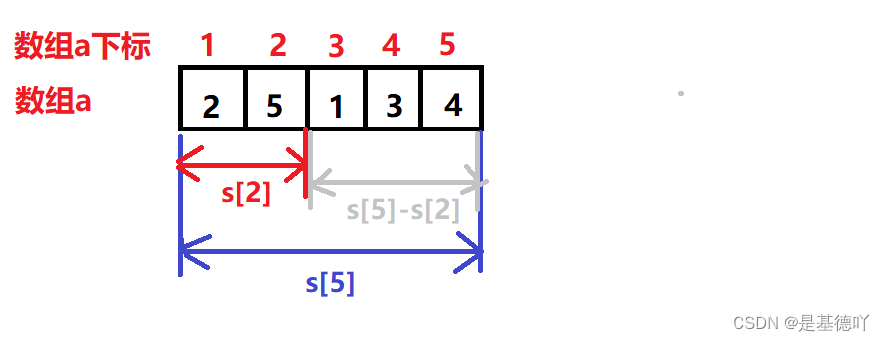
区间和为s[r]-s[l-1]
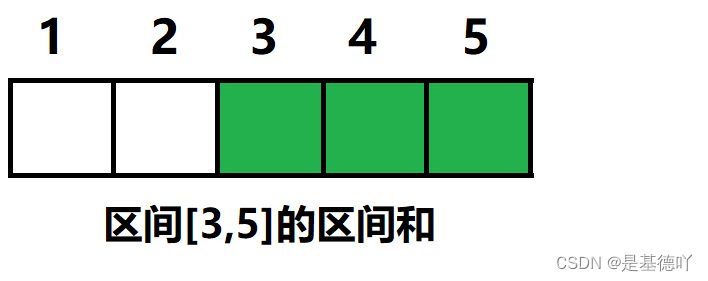
例如下图就表示了区间[3,5]的区间和。
即s[5]-s[2]
while (m--) {int l, r;cin >> l >> r;cout << s[r] - s[l - 1] << endl;
}1.5 模板题
AcWing 795. 前缀和
原题链接:https://www.acwing.com/problem/content/797/
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+10;
ll a[N],s[N];int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,m; cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];s[i]=s[i-1]+a[i]; //求前缀和}while(m--){int l,r;cin>>l>>r;cout<<s[r]-s[l-1]<<'\n'; //求区间和}return 0;
}
1.6 总结
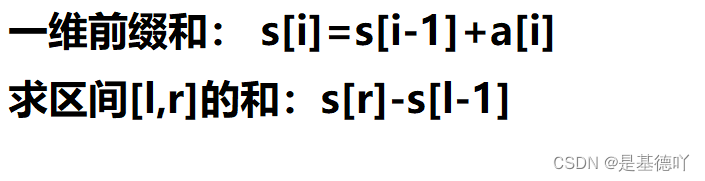
2. 二维前缀和
2.1 定义
一个二维数组a,它的前缀和二维数组s[i][j]表示以(1,1)为左上角元素,以(i,j)为右下角元素的矩形块中所有元素的总和。
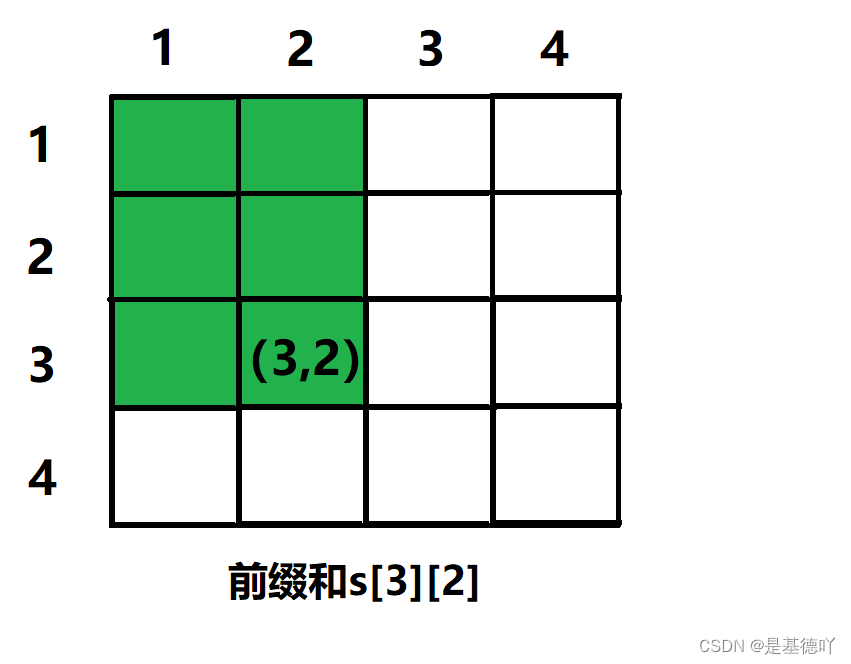
2.2 计算方法
s[i][j]=a[i][j]+s[i][j-1]+s[i-1][j]-s[i-1][j-1]
2.3 模板题
AcWing 796. 子矩阵的和
原题链接:https://www.acwing.com/problem/content/798/
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1010;
ll a[N][N],s[N][N];int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,m,q; cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];s[i][j]=a[i][j]+s[i][j-1]+s[i-1][j]-s[i-1][j-1]; //求二维前缀和}}while(q--){int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;cout<<s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]<<'\n'; //求出子矩阵的和}return 0;
}2.4 总结

3. 一维差分
3.1 定义
差分:很少的询问,但有很多改变数组的操作,每次让不同区间[l,r]内的每个数都加c或者减c
差分是前缀和的逆运算
3.2 差分数组
如果我们要对一个数组分成很多区间,对这些区间做多次操作,每次操作是对某个区间内的所有元素做相同的加减操作,若一个个地修改区间内的每个元素,非常耗时。
这里我们就引入“差分数组”的概念。
差分数组,顾名思义,就是由原数组的两个元素作差得到。
这里我们令原数组为a,数组长度为n,再引入一个数组d表示差分数组,那么我们就可以通过遍历数组a,从而求得差分数组d。
for (int i = 1; i <= n; i++) {d[i] = a[i] - a[i - 1];
}差分数组的前缀和是原数组
3.3 差分标记
假设我们要修改的区间为[l,r] ,差分数组为d,我们要让[l,r]区间的每个数都加c。
我们就打标记:
d[l] += c;
d[r + 1] -= c;原理:某一位+c,会把这个操作带到后面。
3.4 作用
引入差分数组d,当修改某个区间时,只需要修改这个区间的端点,就能记录整个区间的修改,而对端点的修改非常简单,复杂度为O(1)。
当所有修改操作结束后,再利用差分数组计算出新的原数组。
3.5 适用场景
长度为n的数组a,1次询问,m次操作,每次令区间[l,r]的每个数+c或-c。
3.6 模板题
AcWing 797. 差分
原题链接:https://www.acwing.com/problem/content/799/
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+10;
ll a[N],d[N];int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,m; cin>>n>>m;for(int i=1;i<=n;i++) {cin>>a[i];d[i]=a[i]-a[i-1]; //求差分数组}while(m--){int l,r,c;cin>>l>>r>>c;d[l]+=c; //差分标记d[r+1]-=c;}for(int i=1;i<=n;i++){d[i]=d[i-1]+d[i]; //差分数组前缀和cout<<d[i]<<' ';}return 0;
}4. 二维差分
4.1 定义
n行m列的矩阵,左上角数组元素坐标为(x1,y1),右下角数组元素坐标为(x2,y2),1次询问,m次操作,每次操作让矩阵的所有元素都加c或者减c。
4.2 差分数组
设原数组为n行m列的二维数组a,差分数组为d。

for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){d[i][j]=a[i][j]-a[i][j-1]-a[i-1][j]+a[i-1][j-1];}
} 4.3 差分标记
假设我们要修改的矩阵的左上角元素坐标为(x1,y1),右下角坐标为(x2,y2),差分数组为d,我们要让这个矩阵内的每个数都加c。
我们就打标记:
d[x1][y1]+=c;
d[x1][y2+1]-=c;
d[x2+1][y1]-=c;
d[x2+1][y2+1]+=c;4.4 模板题
AcWing 798. 差分矩阵
原题链接:https://www.acwing.com/problem/content/800/
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1010;
ll a[N][N],d[N][N];int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,m,q; cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];d[i][j]=a[i][j]-a[i][j-1]-a[i-1][j]+a[i-1][j-1]; //求差分数组}} while(q--){int x1,y1,x2,y2,c;cin>>x1>>y1>>x2>>y2>>c;d[x1][y1]+=c; //差分标记d[x1][y2+1]-=c;d[x2+1][y1]-=c;d[x2+1][y2+1]+=c;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){d[i][j]=d[i][j]+d[i][j-1]+d[i-1][j]-d[i-1][j-1]; //差分数组前缀和cout<<d[i][j]<<' ';}cout<<'\n';}return 0;
}