一)红黑树的基本概念和基本性质:
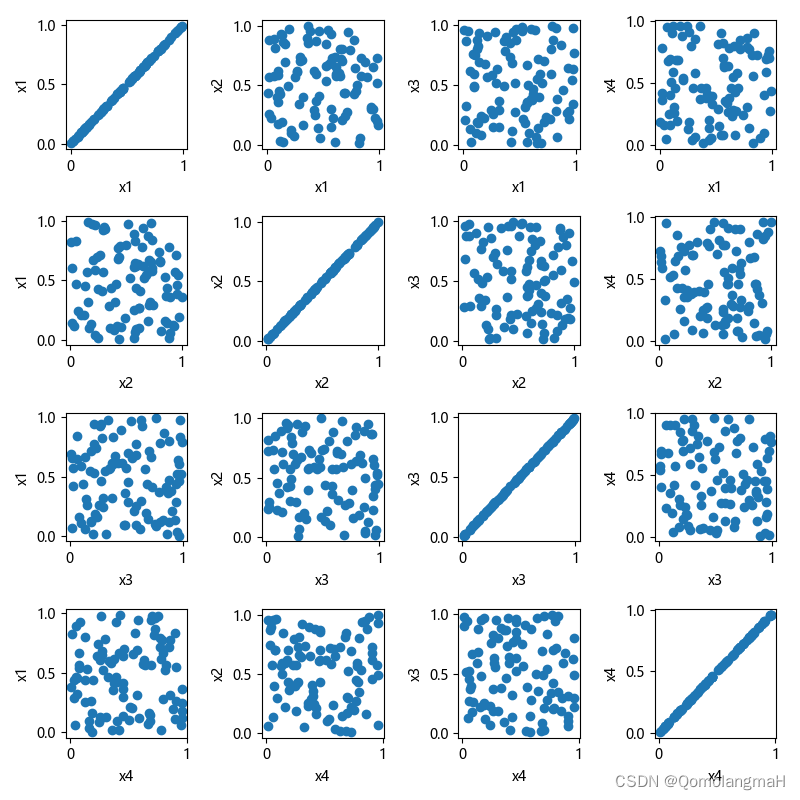
1)红黑树就是一种高度平衡的二叉搜索树,但是在每一个节点上面都增加了一个存储位来表示结点的颜色,可以是红色或者是黑色,通过对任何一条从根节点到叶子节点上面的路径各个节点着色方式的限制,红黑树会自动确保没有一条路经会比其他路径的长度高出两倍,而是接近平衡的
2)红黑树最长路径是最短路径的两倍
3)每一个节点不是红色就是黑色
4)根节点是黑色的
5)如果一个节点是红色的,那么他的左右孩子的节点都是黑色的,说明红黑树没有两个连续相同的红色节点
6)对于每一个节点,从该节点到达后代的叶子结点的所有简单路径里面,均包含相同数目的黑色节点(每一条路径上都包含着相同数目的黑色节点,路径的计算必须指向空)
在红黑树中,对于每个节点,从该节点到其所有后代叶子节点的简单路径上,应包含相同数量的黑色节点,这也是红黑树的基本性质之一。
在计算路径上的黑色节点数量时,通常会包括空节点(NIL节点)因为空节点被视为黑色节点的一部分,并且它们对于保持红黑树的平衡性和性质是必要的,所以,在判断从任意节点到达后代叶子节点的所有简单路径是否包含相同数量的黑色节点时,应该将空节点(NIL节点)也计算在内
7)每一个叶子节点都是黑色的,此处的叶子节点指的是空节点
8)红黑树的最长路径:路径上节点黑红相间,一黑一红,最短路径:路径上全部是黑色节点
9)假设黑色节点总共有X个,整棵树的节点数量在[X,2X]之间
当总节点个数是X个的时候最短路径的长度:logX
当总结点个数是2X的时候最短路径长度是:logX+1,logX趋近于logN
所以最终总结:
最短路径长度为:logN
最长路径长度为:2logN
10)一个正常的二叉树,不会出现这种一条路径全部都是黑色的情况
二)红黑树的插入:
1)首先要明白,插入的节点必须是红色的节点,如果最终插入的是黑色的节点,因为我们要最终保证每一条路径上都有数目相同的黑色节点,其他路经都必须得新增黑色节点,但是此时新插入的是一个黑色节点,其他路经也没有办法新增节点呀,但是此时就不满足一个条件,两个红色节点挨在一起了,所以需要调节成合适的颜色
2)红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可以分为两步
2.1)按照二叉搜索树的规则插入新节点
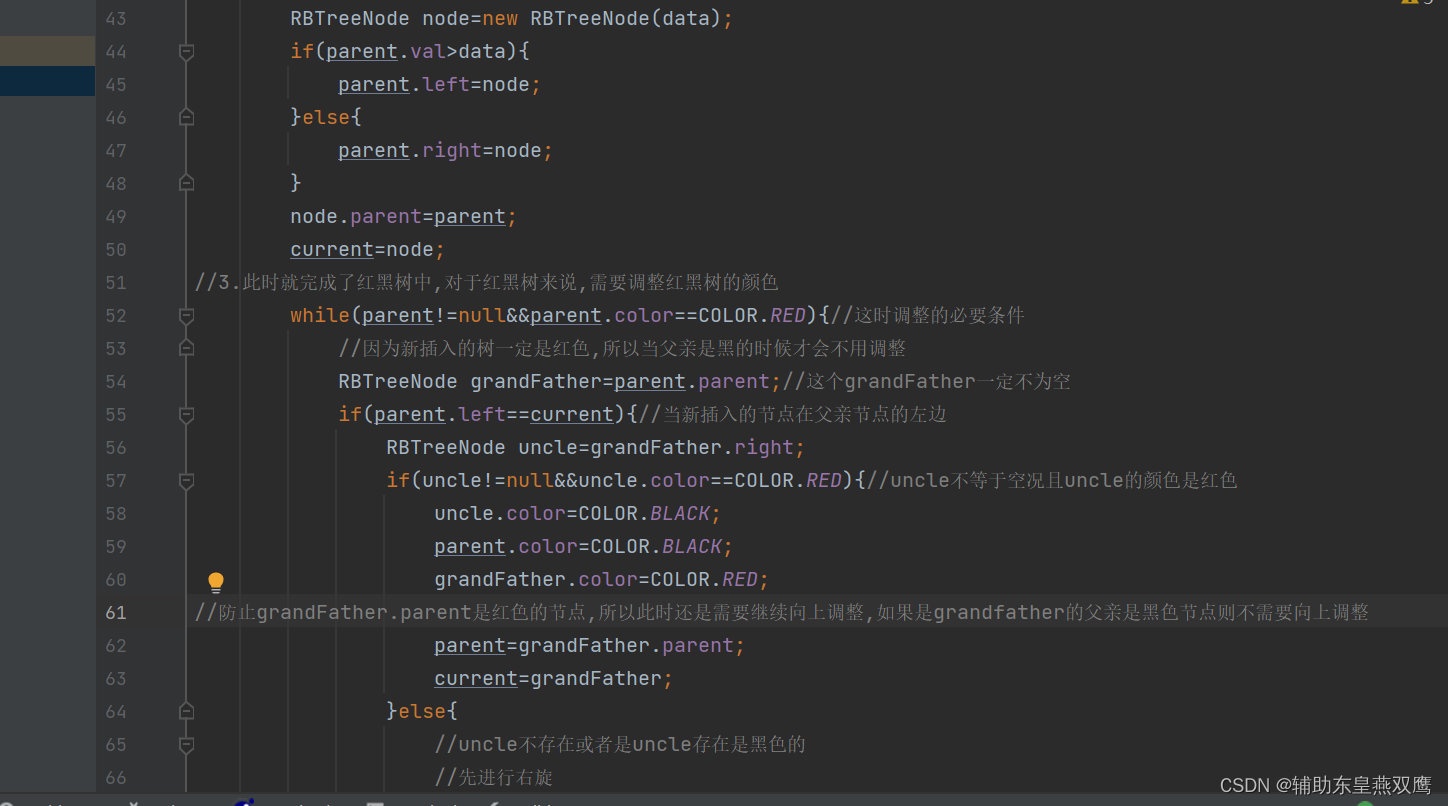
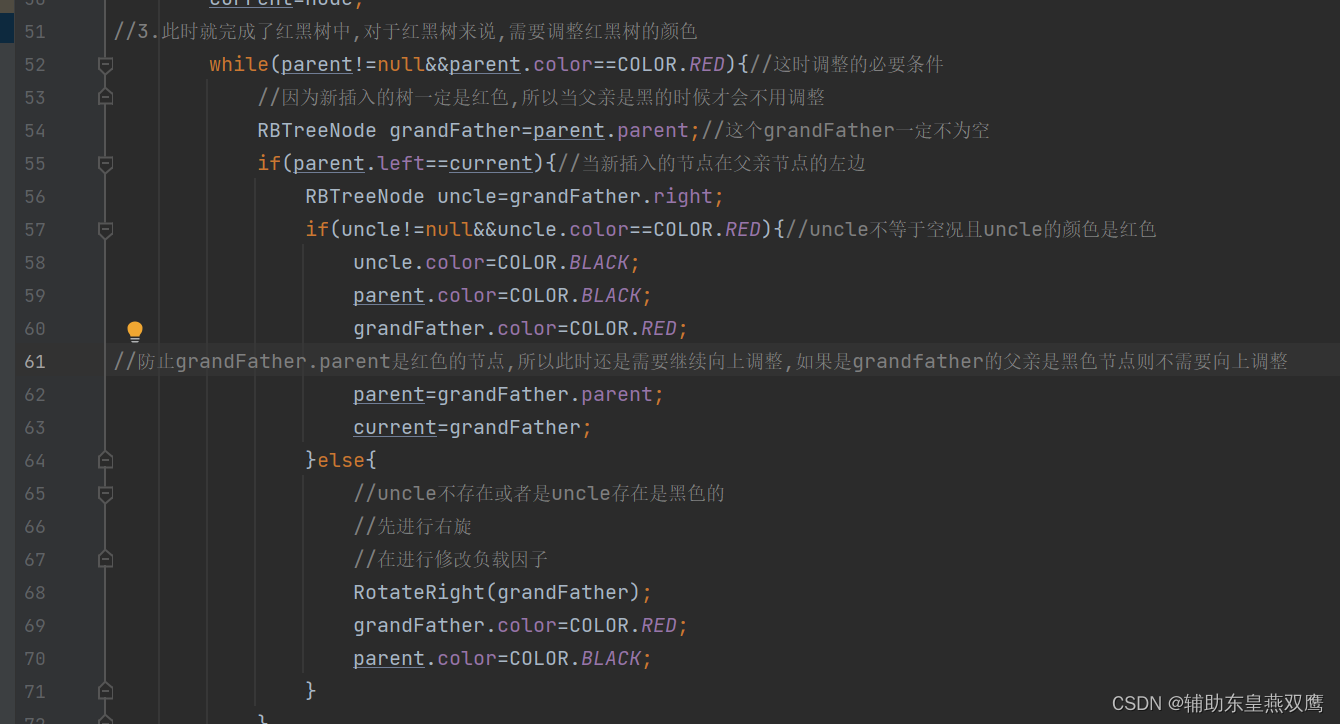
2.2)检测插入新节点之后,判断红黑树的性质是否已经遭受到了破坏,因为新节点的默认颜色是红色,因此如果双亲结点的颜色是黑色,那么其实本质上并没有违反红黑树的任何性质,那么就不需要进行调整,但是当插入的新节点的双亲结点是红色的时候,就违反了不能有连在一起的红色节点,此时需要对红黑树来分情况进行讨论:
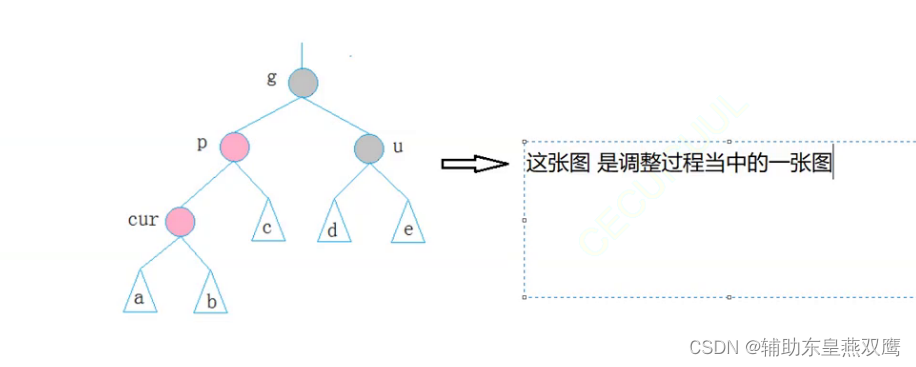
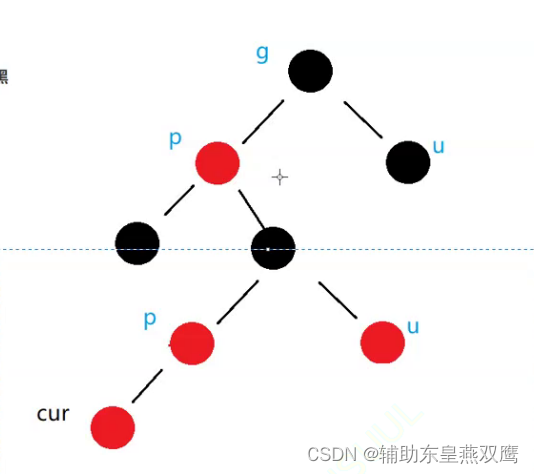
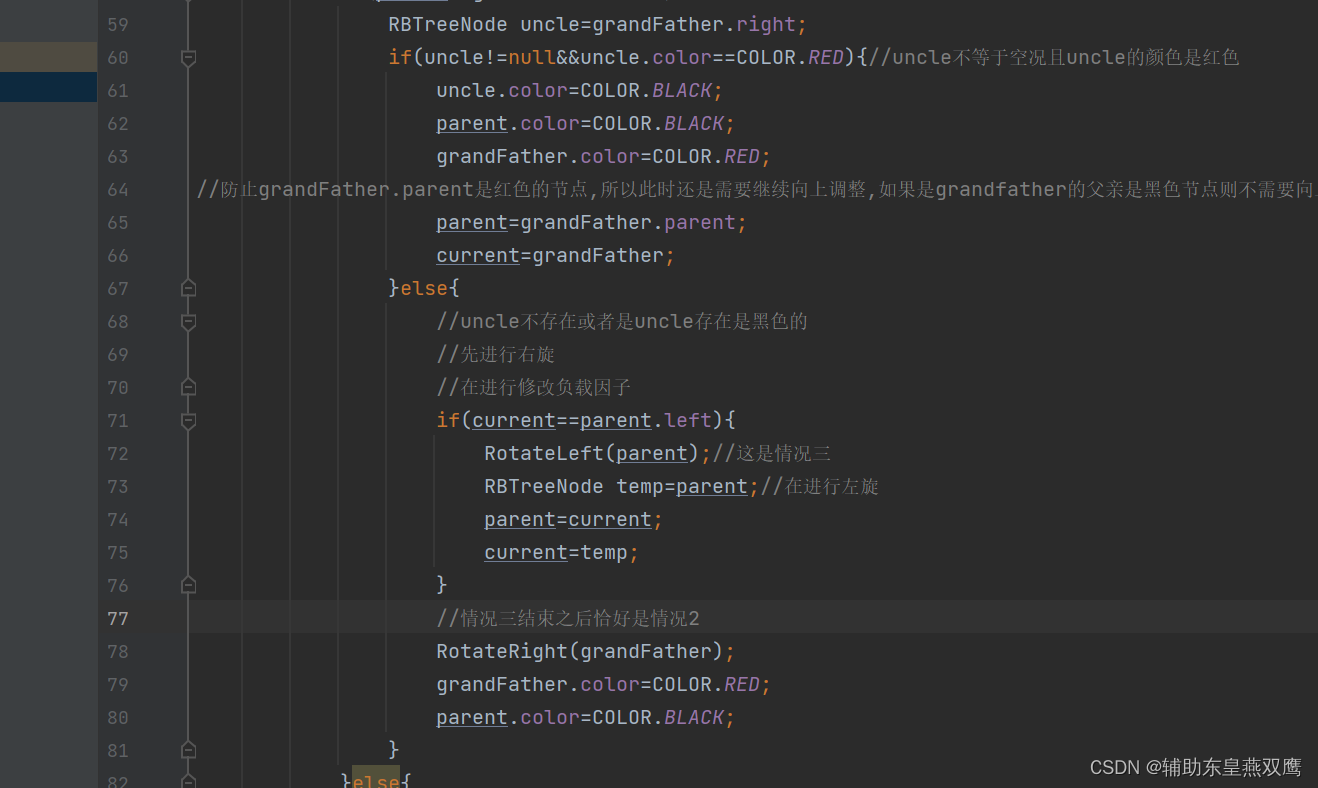
约定current为当前新插入的节点,parent为父亲节点,grandfather是祖父节点,uncle为叔叔节点
一)一共是有两种大的情况:parent是在grandfather的left节点:
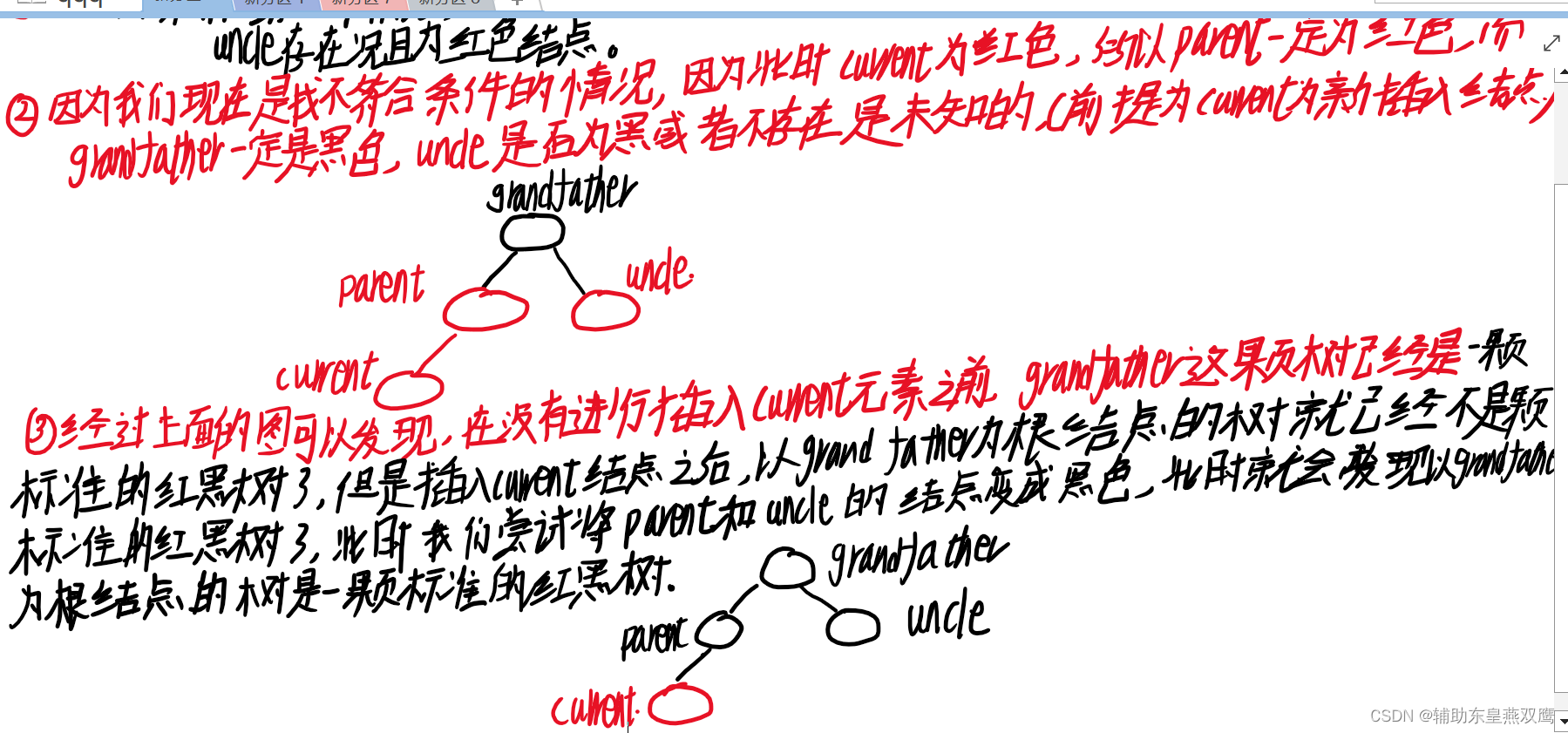
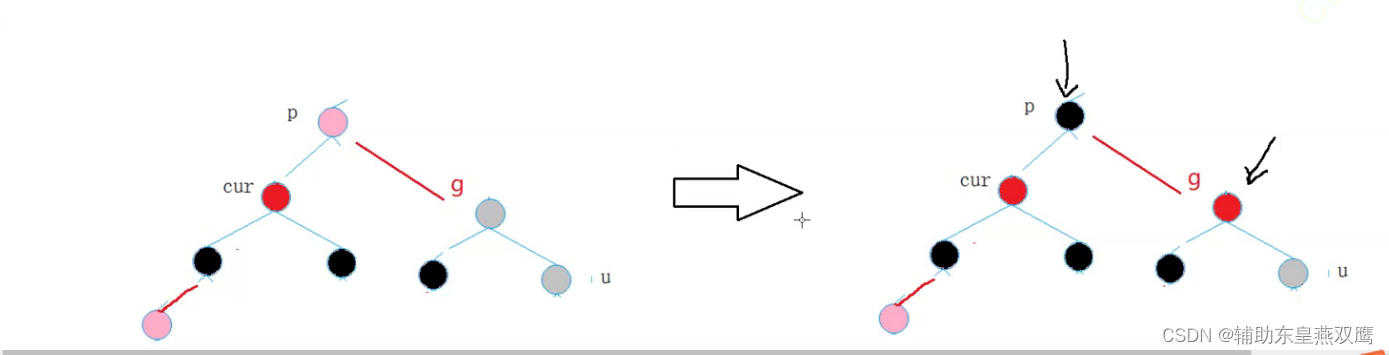
1)current为红色节点,parent是红色节点,grandfather是黑色节点,uncle存在是红色节点,下面都是默认讨论curent是parent的左子树,但是实际情况current下可能是parent的左子树,还有可能是parent的右子树;
1.1)下面只是考虑到了grandfather以下的节点:发现只需要把parent节点和uncle节点变成黑色,就可以简单的满足以grandfather为根节点的树,从根节点到叶子节点的树是一颗标准的红黑树,此时gp的左子树一定是有一个黑色节点的;
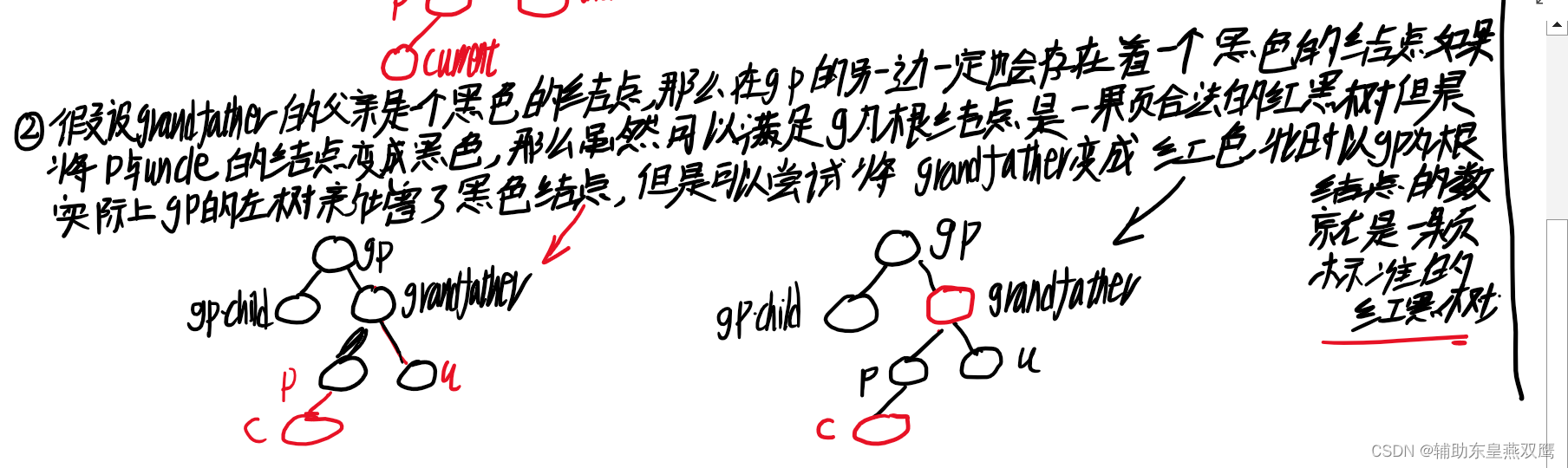
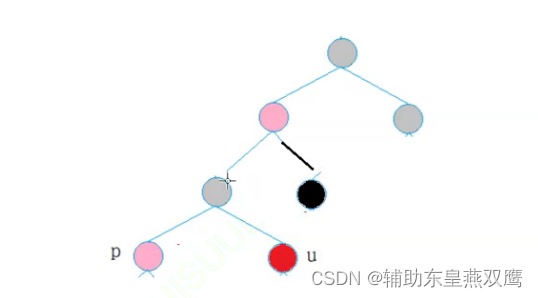
1.2)第二个横线更深一步考虑,当考虑到granfather的父亲节点的时候,当grandfather的父亲节点是黑色的时候或者是grandfather节点是红色的时候,需要再进一步分情况进行讨论:
1.3)当grandfather的父亲节点是黑色的时候说明,grandfather的另一个孩子也是黑色节点
此时如果将grandfather的这个节点的父亲节点是一个黑色的节点那么如果只是单纯的将p和u变成黑色是万万不可以的,这样只会增加黑色节点的个数
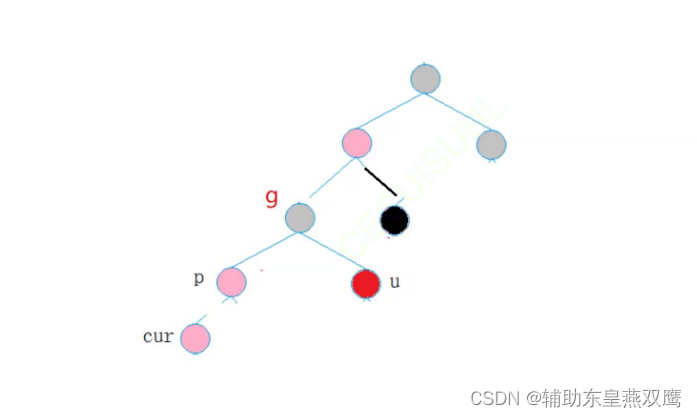
1.4)假设grandfather的父亲节点是红色,此时可以分析出gp的左孩子一定是黑色的
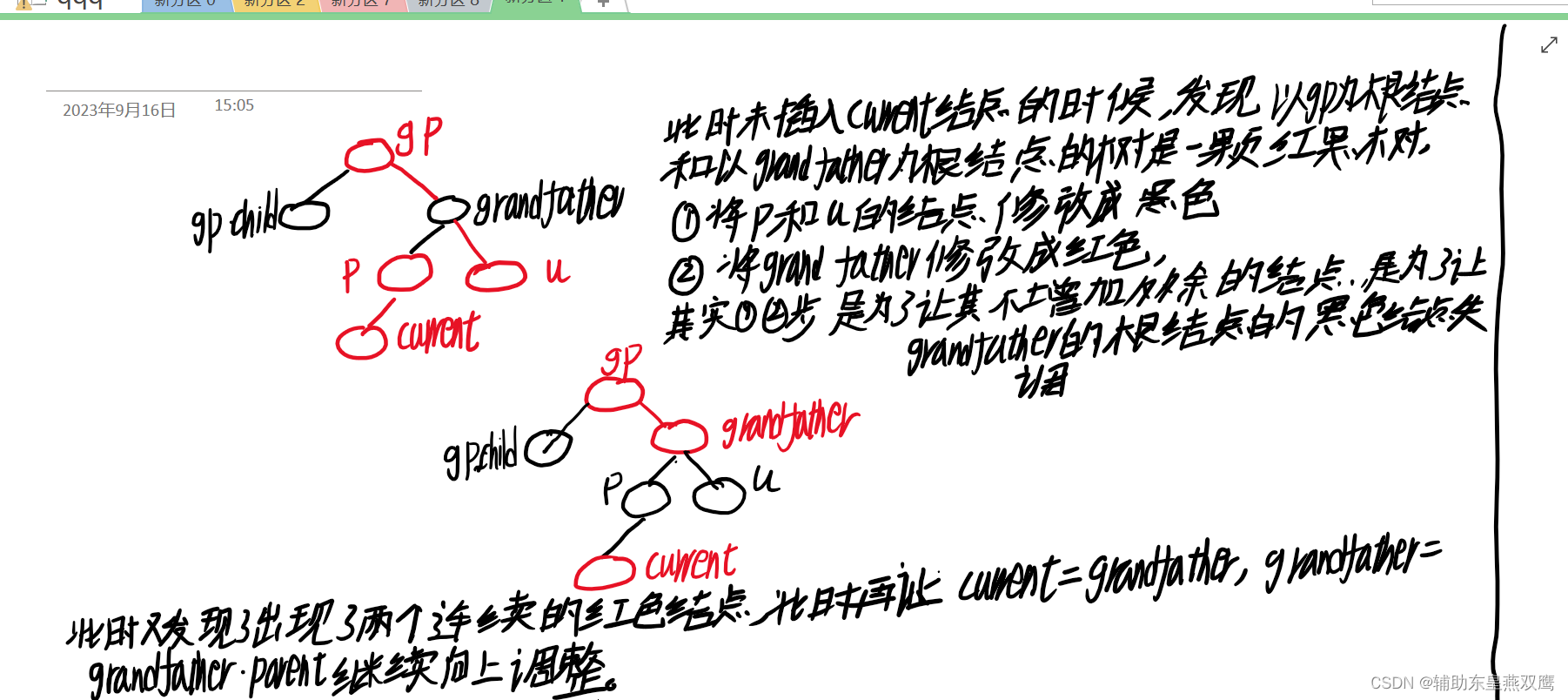
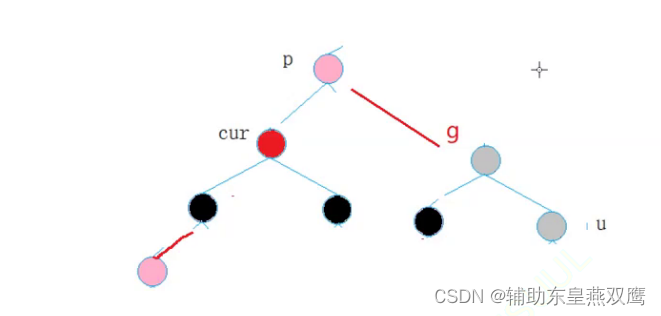
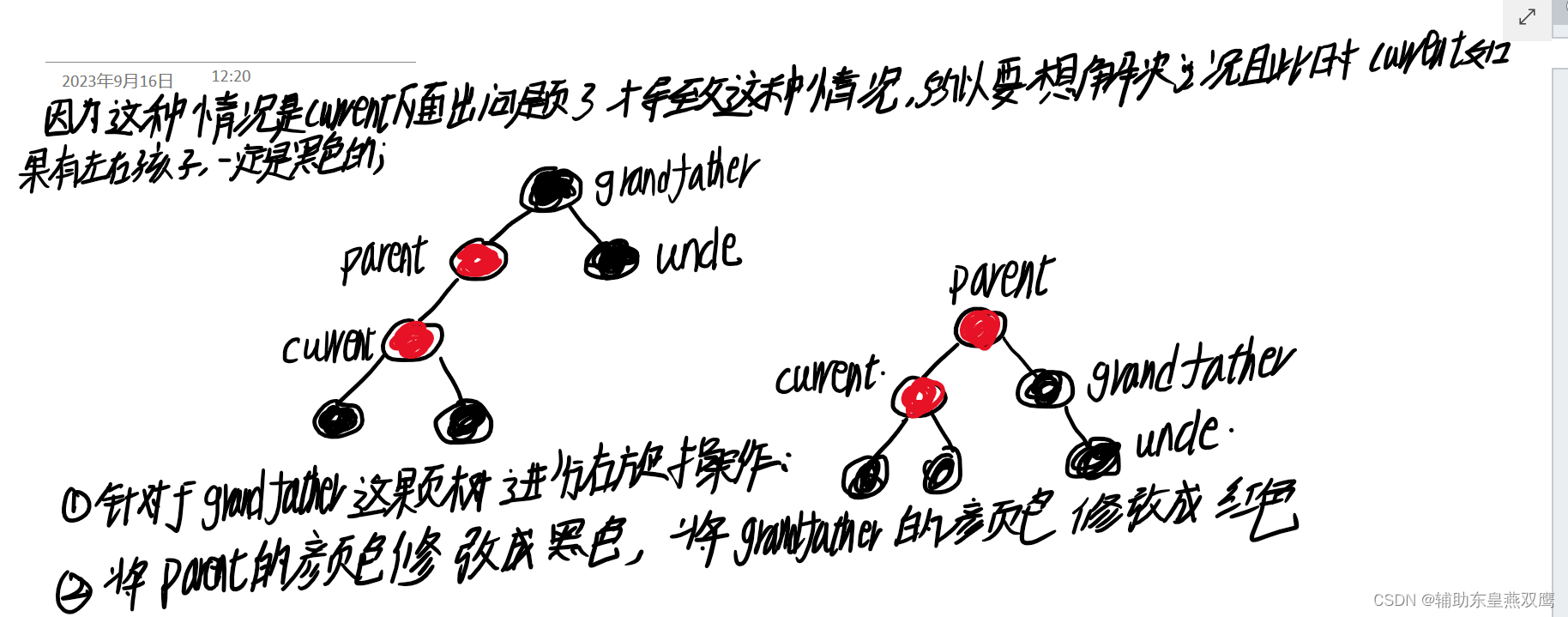
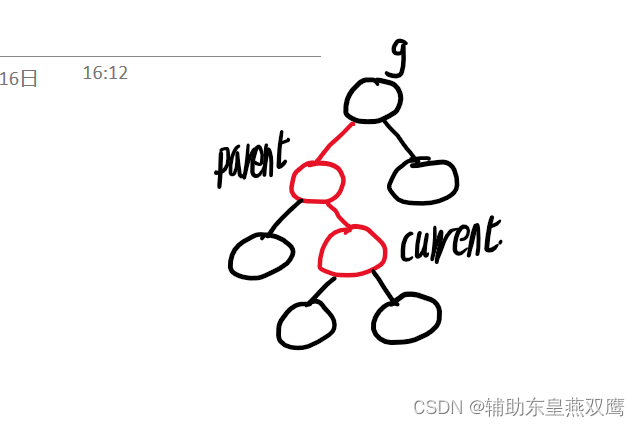
2)current为红色,parent是红色,grandfather是黑色,uncle不存在或者是uncle是黑色
此时current下面一定有子树其他节点:是再调整的过程中current变成红色的
先进行右旋:
然后修改颜色:
3)current是红色,parent是红色,grandFather是黑色,uncle不存在或者uncle是黑色
二)第二种情况parent是在grandfather的right节点: