在这里插入图片描述
Halo，这里是Ppeua。平时主要更新C++，数据结构算法，Linux与ROS…感兴趣就关注我bua！

文章目录

0.平衡搜索二叉树概念
- 0.1 平衡因子
1.插入
- 1.1 普通插入操作
- 1.2更新平衡因子
2.旋转
- 2.1 左单旋
- 2.2 右单旋
- 2.3 右左双旋
- 2.4 左右双旋
3. 旋转判定
4. 验证是否为AVL树
5.完整源码(AVL插入旋转)

在这里插入图片描述

0.平衡搜索二叉树概念

为什么在会了搜索二叉树之后,还需要学习平衡搜索二叉树呢？在搜索二叉树部分,并没有要求树保持平衡,仅需遵循左小右大即可.

若往树中插入有序或者接近有序的值,会出现下面这种情况,退化为单支树.

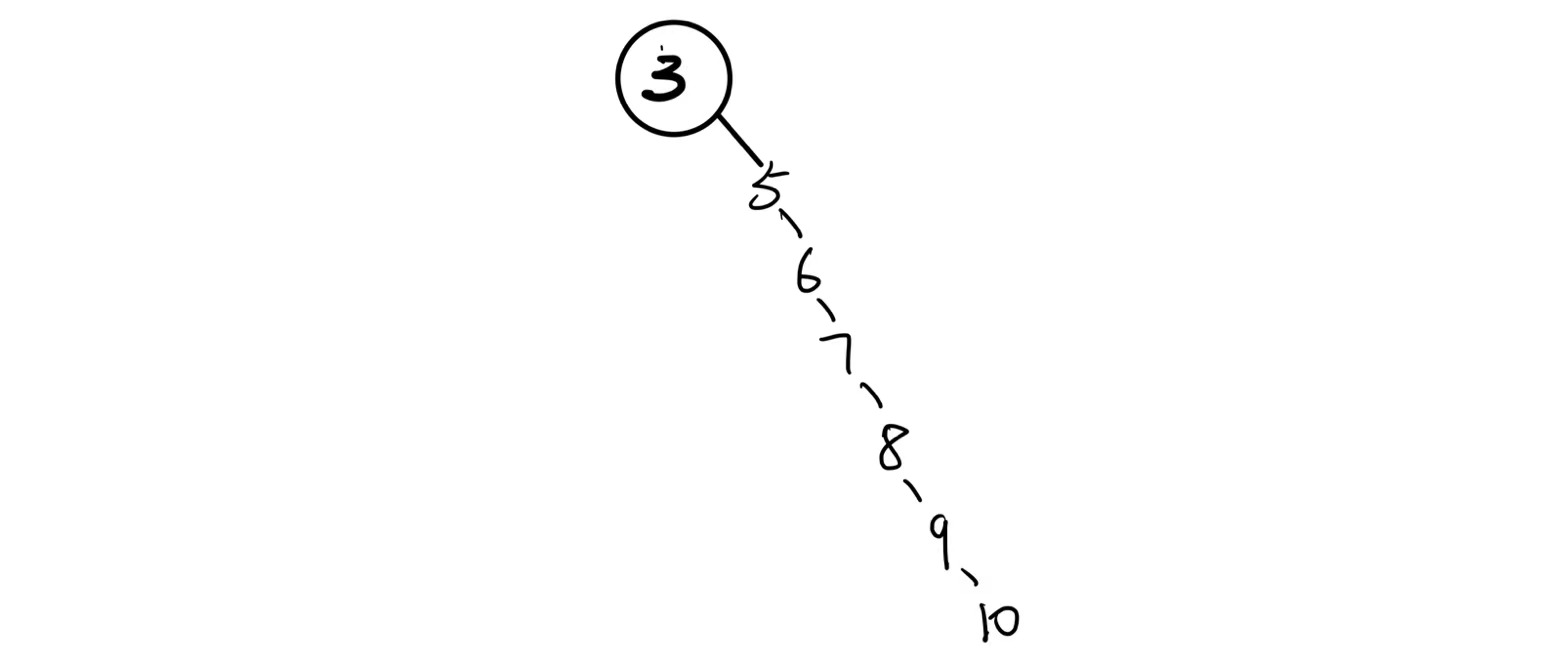
f5e6a0c761ccc48519e7d23748aaeea

这样的搜索树就完全没有效率可言,他的时间复杂度为o(N).所以我们需要一棵正常(平衡)的树来解决这个问题.

否则当map和set用这样的树岂不是效率非常的低,所以这就是平衡二叉搜索树的意义.

将子树的左右平衡高度差维持在(-1/0/1)之间,若超过了这个范围,则对树进行高度调整,从而减少搜索长度.

上面的那棵树可以变化成这个样子,这样搜索的效率就变成了o(logN),大大提高了效率.

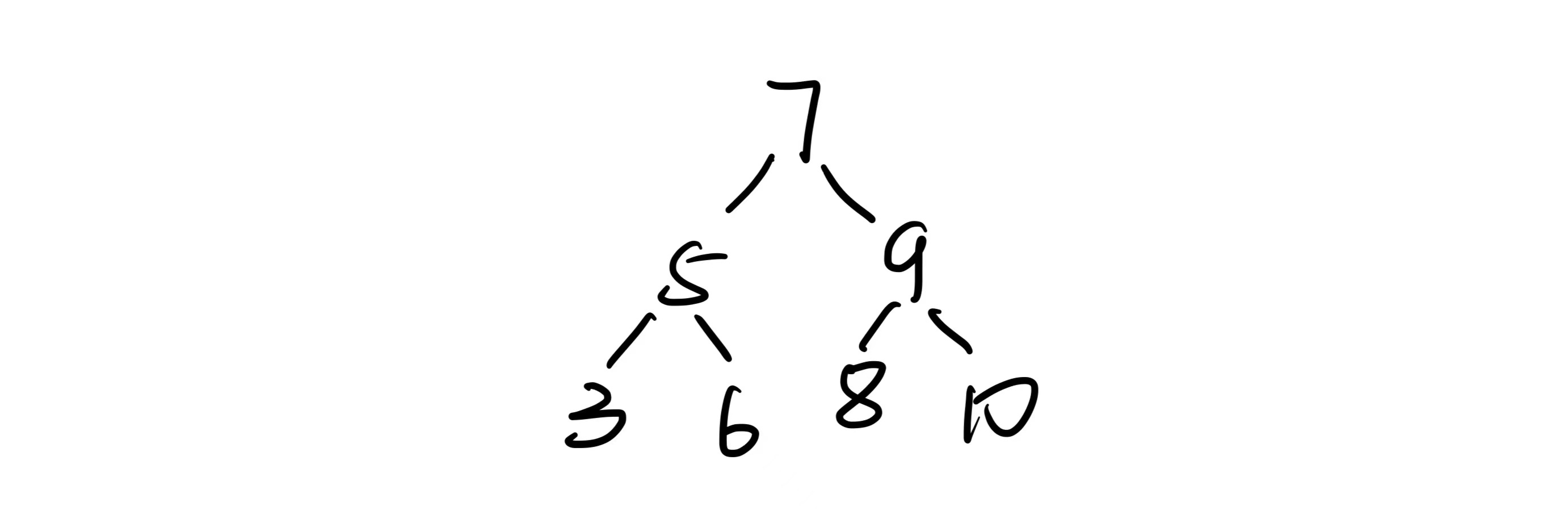
52a0ba283e5ccbecd31c8b27f781b32

这同样是一棵满二叉树.其节点个数为 $2^h-1$ ,可以将其看作一颗特殊的平衡二叉搜索树.

所以平衡二叉搜索树的节点个数的公式为: $2^h-X$ ,X的范围介于[1, $2^{(h-1)}-1$ ]之间.

这里可以这样理解.二叉树的最大深度差为1,此时的最后一层最差的情况为只有一个节点,那么缺少的节点数为前面所有层的节点.

忽略掉常数,可以看到h可以近似等于logN.

0.1 平衡因子

上文提到,二叉搜索树需要计算其平衡因子来稳定树的平衡度.那么平衡因子怎么算呢?

左子树的最大高度为负,右子树的最大高度为正.两值相加,体现在根上的即为这棵树的平衡因子

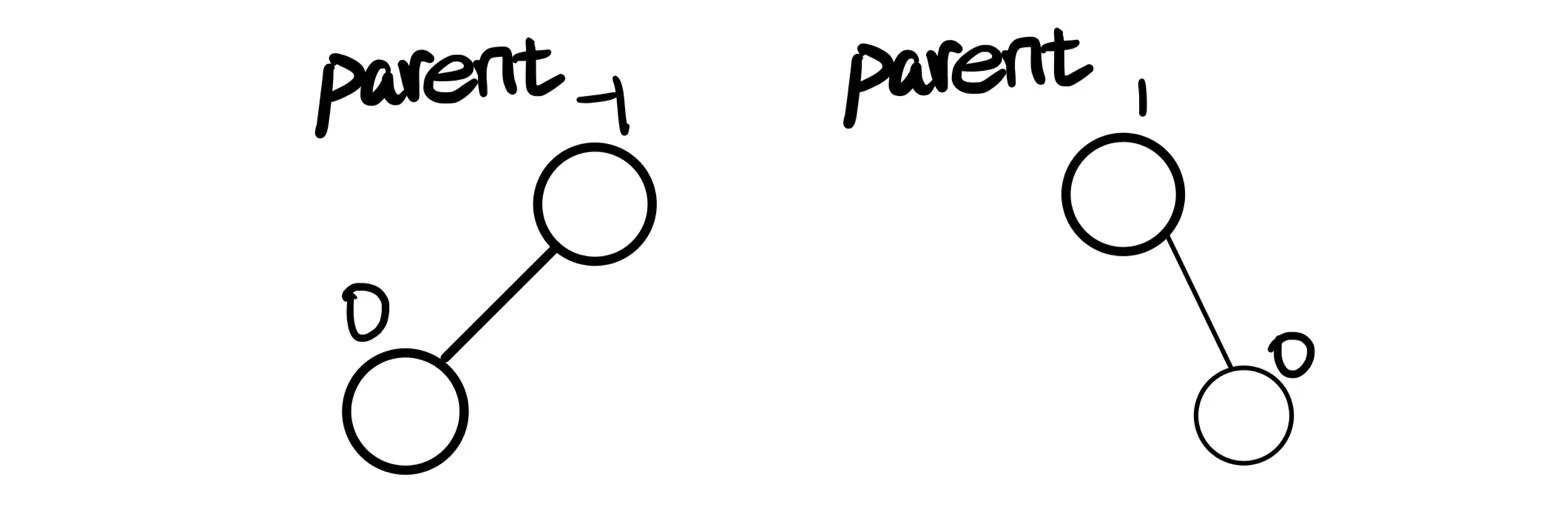
72d1ee6e5abfb6956df96f1d6a2bf42

因为其对树的结构调整,需要大量访问parent,也就是子树的根,所以在定义这棵树的时候.我们直接将其parent存起来,方便后续查找.

template<typename K,typename V>
struct TreeNode
{	pair<K, V>_val;TreeNode<K,V>* _left;TreeNode<K,V>* _right;TreeNode<K,V>* _parent;int _bf;TreeNode(const pair<K,V> val):_val(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};

1.插入

我们先写一个最简单的二叉树插入操作,然后在上面加上平衡因子的更新与旋转即可.

1.1 普通插入操作

bool Insert(const pair<K, V> kv){Node* parent = _root;Node* cur = _root;if (_root == nullptr){_root = new Node(kv);}while (cur){if (kv.first > cur->_val.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_val.first){parent = cur;cur = cur->_left;}else return false;;}cur = new Node(kv);if (parent->_val.first > kv.first){parent->_left = cur;}elseparent->_right = cur;cur->_parent = parent;}

1.2更新平衡因子

当我们插入一个新的节点的时候,**新增在左则平衡因子减减,新增在右则平衡因子加加.**此时有以下这几种情况:

当更新完平衡因子,parent的平衡因子为0时,说明并没有引起这棵子树的高度变化.则不需要继续向上更新平衡因子
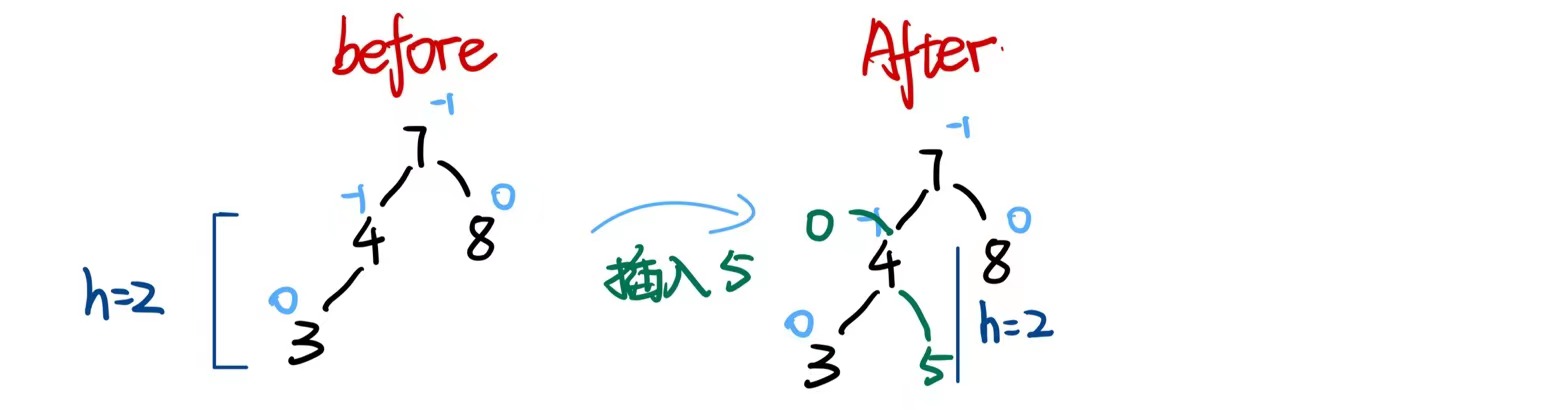
当更新完平衡因子,parent的平衡因子为-1/1时,说明引起了这棵树的高度变化,需要继续更新其祖先的平衡因子
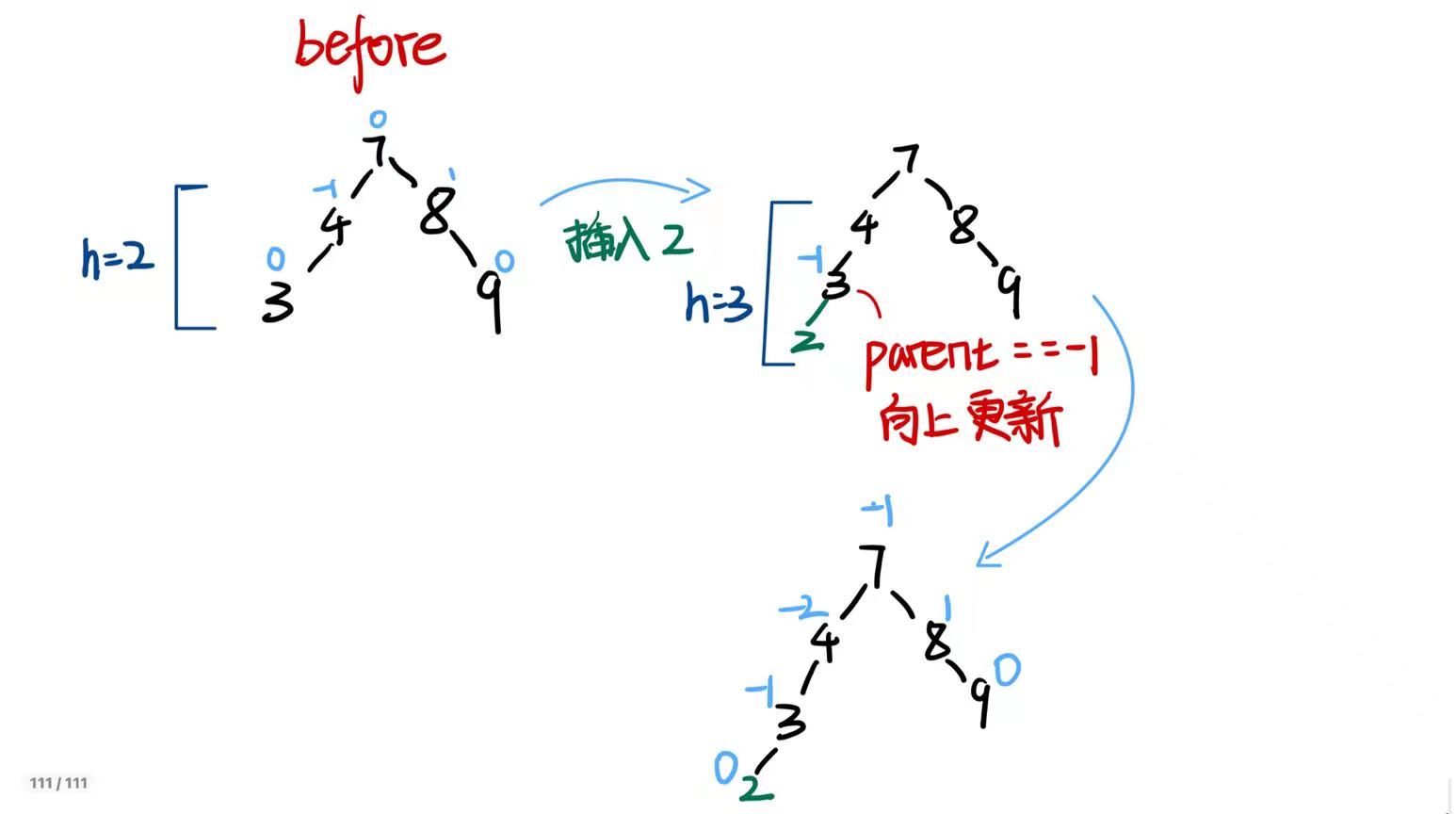
当更新完平衡因子,parent的平衡因子为-2/2时,说明这棵树需要进行旋转来维持平衡

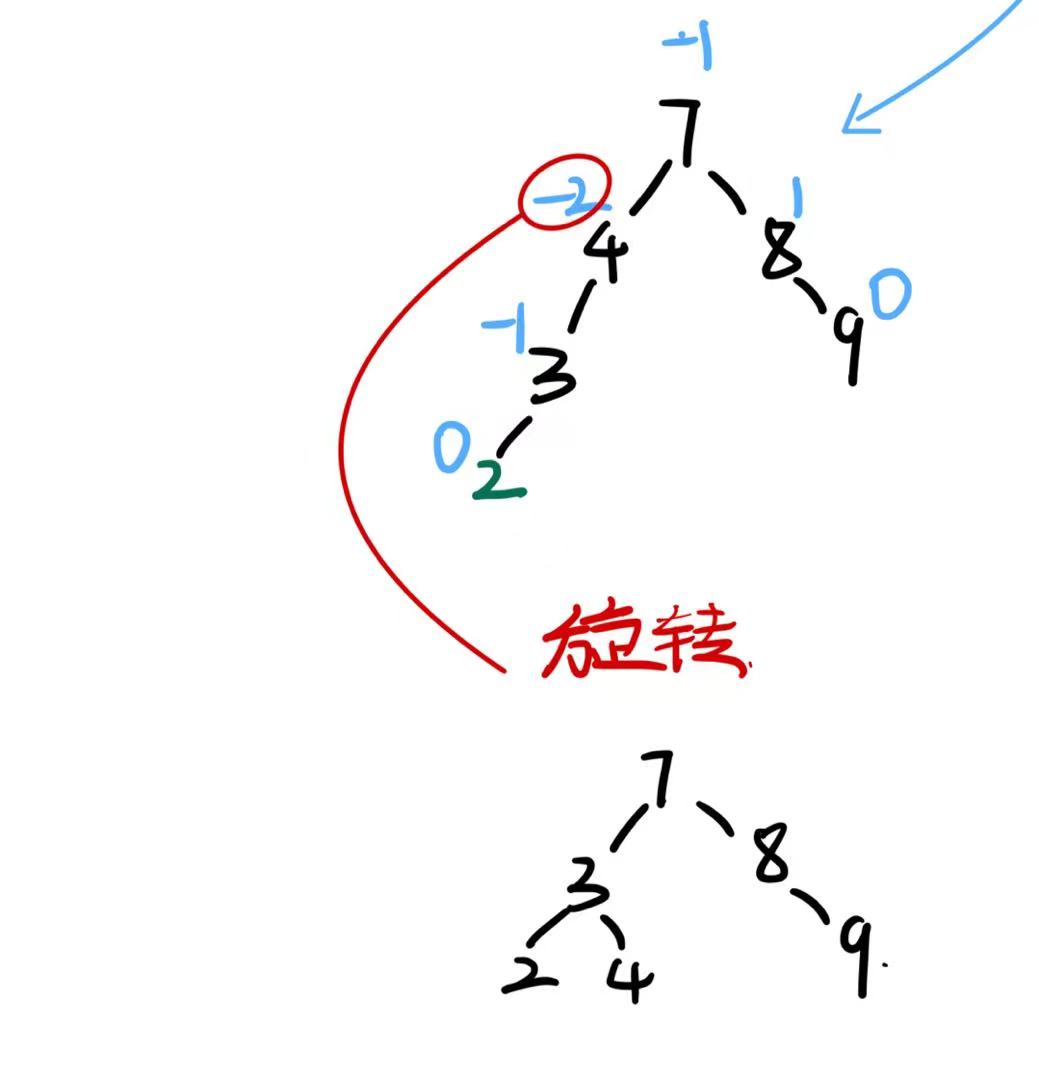
关于旋转我们稍后再说,我们在代码里加上更新平衡因子的这几步操作.

while (parent)
{if (parent->_left == cur){parent->_bf--;}else parent->_bf++;if (parent->_bf == 0)break;else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent=parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){//旋转}
}

2.旋转

旋转根据实际的情况,可以分为四种情况:左单旋,右单旋,左右单旋,右左单旋

旋转的目的是:在不破坏AVL的前提下,降低这棵树的高度,使其重新成为AVL树

2.1 左单旋

当parent节点的平衡因子为2时,需要进行左单旋来降低整棵树的高度.

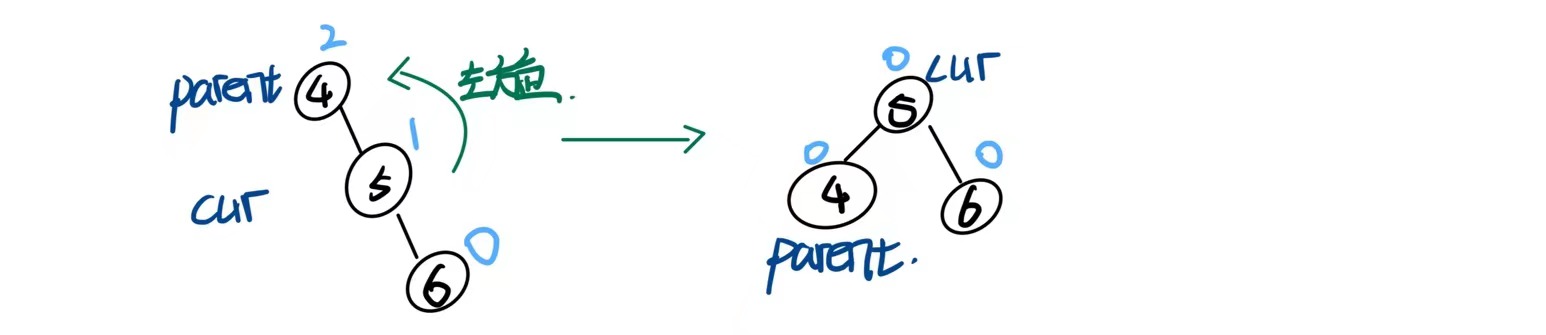
99f00fa3799b2eb8388f04c146961d8

这是最简单的情况,即让parent->right=cur->left cur->left=parent

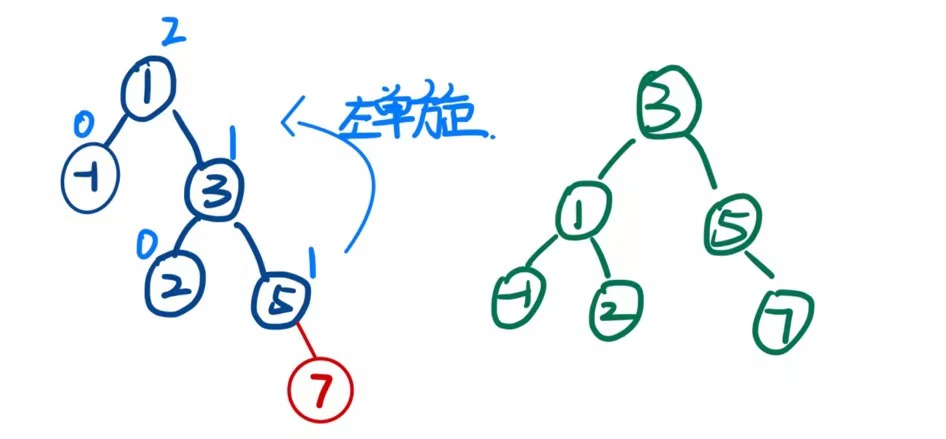
e51ff0434783fd26331ced235bc266a

当需要旋转的是一颗子树的时候,核心操作不变,但需要更新下parent 与 pparent的关系,将pparent指向cur

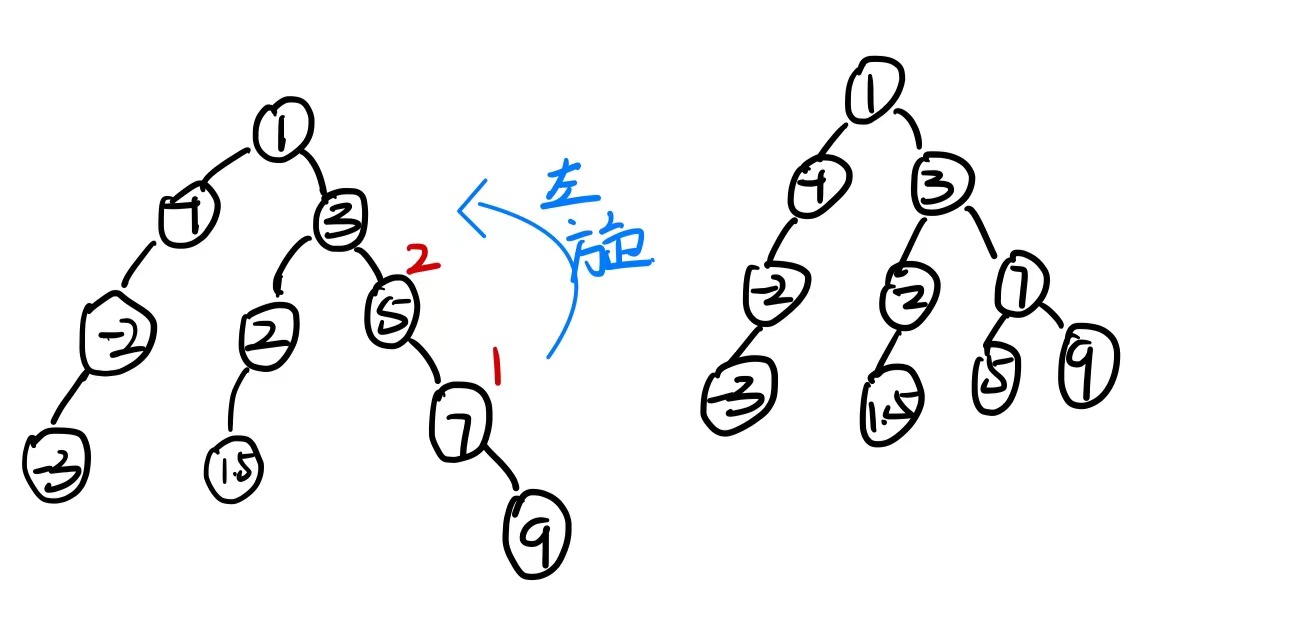
95086d741a40aaa01aa14227dee4ba0

所以左单旋的代码也可以写出来了

void RotateL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;if (curleft)curleft->_parent = parent;parent->_right = curleft;cur->_left = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (_root == parent){cur->_parent = nullptr;_root = cur;}else{if (pparent->_left == parent){pparent->_left = cur;}else pparent->_right = cur;cur->_parent = pparent;}parent->_bf =cur->_bf= 0;
}

2.2 右单旋

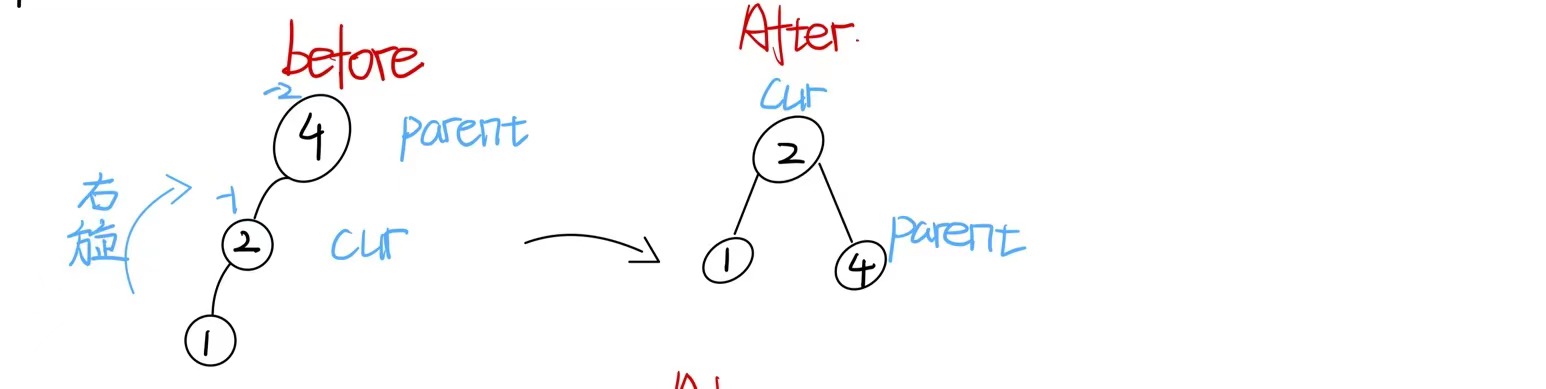
0204c9ebc93ddd12b6a1fc6aa9e9904

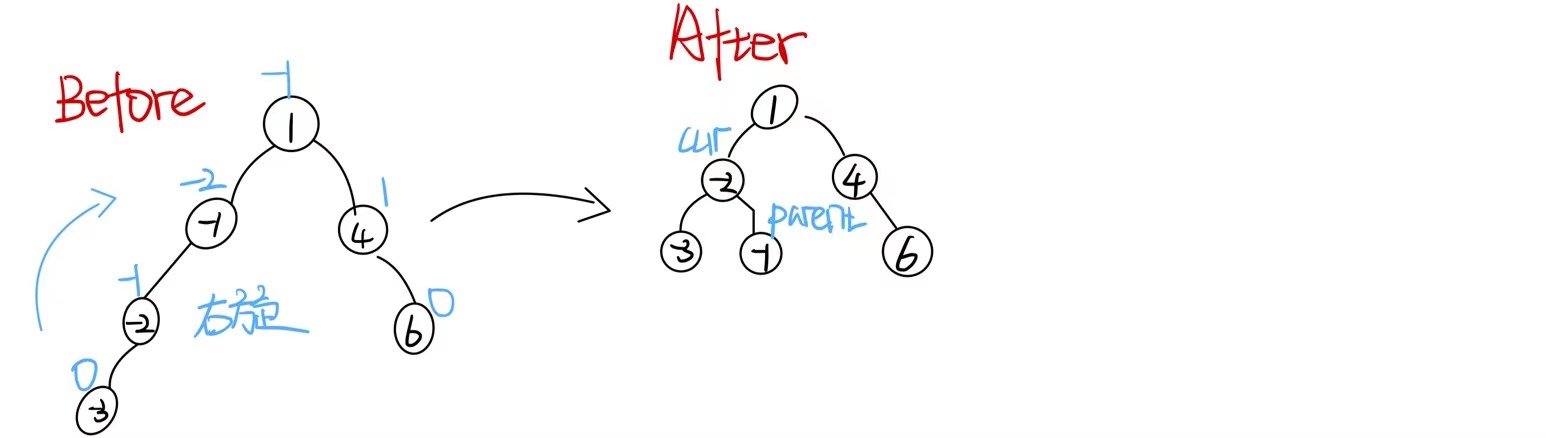
38eb9e421d098c02a98833aeff6a835

其旋转核心为:**parent->left=cur->right cur->right=parent **

所以右旋转的代码为:

void RotateR(Node* parent)
{Node* cur = parent->_left;Node* curleft = cur->_left;if (curleft){curleft->_parent = parent;}parent->_left = curleft;if (parent == _root){cur->_left = parent;}else{Node* pparent = parent->_parent;if (pparent->_left = parent){pparent->_left = cur;}elsepparent->_right = cur;cur->_parent = pparent;}parent->_bf = cur->_bf = 0;parent->_parent = cur;}

2.3 右左双旋

其抽象模型为:

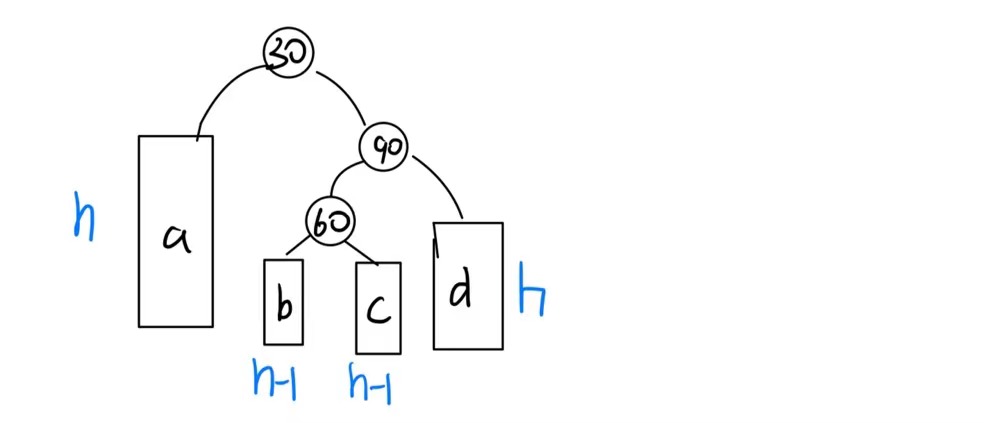
77c0d0a19775931dbca542aafecfe67

这个模型实在有点抽象,我们分以下几种情况来讨论.

当h0时,此时60为插入的节点(60->bf0)

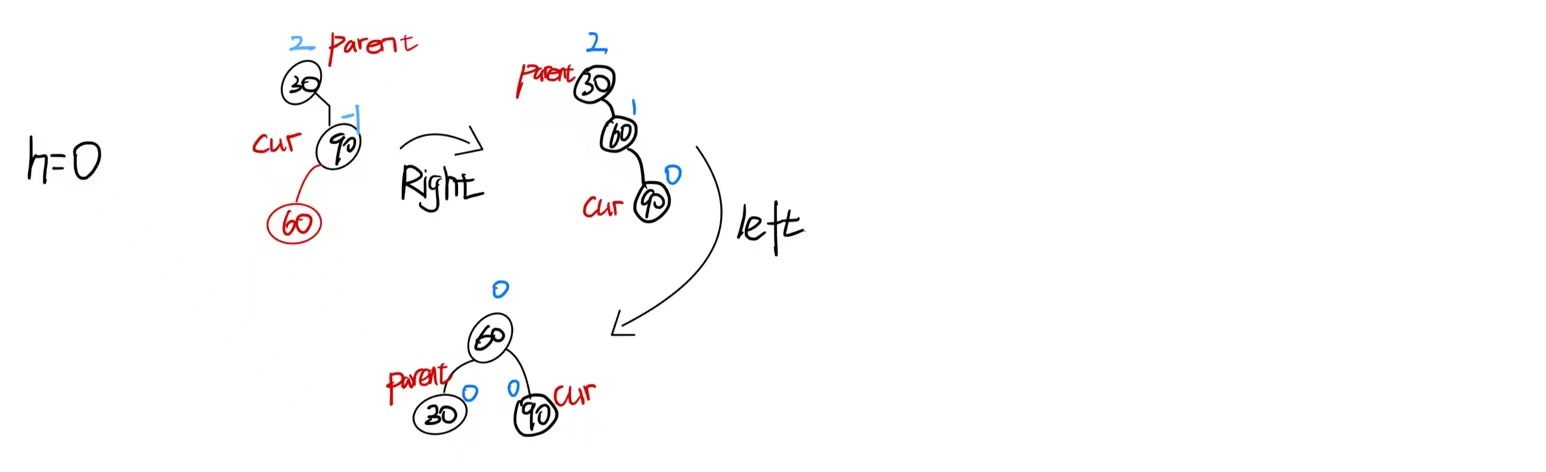
deb3c319d89ed5b7e1b7ab7947f59f6

旋转完成后,parent->bf cur->bf均为0

当h==1时,此时可以分为在60的左边插入或者在60的右边插入

在左边插入(curleft->bf==-1)

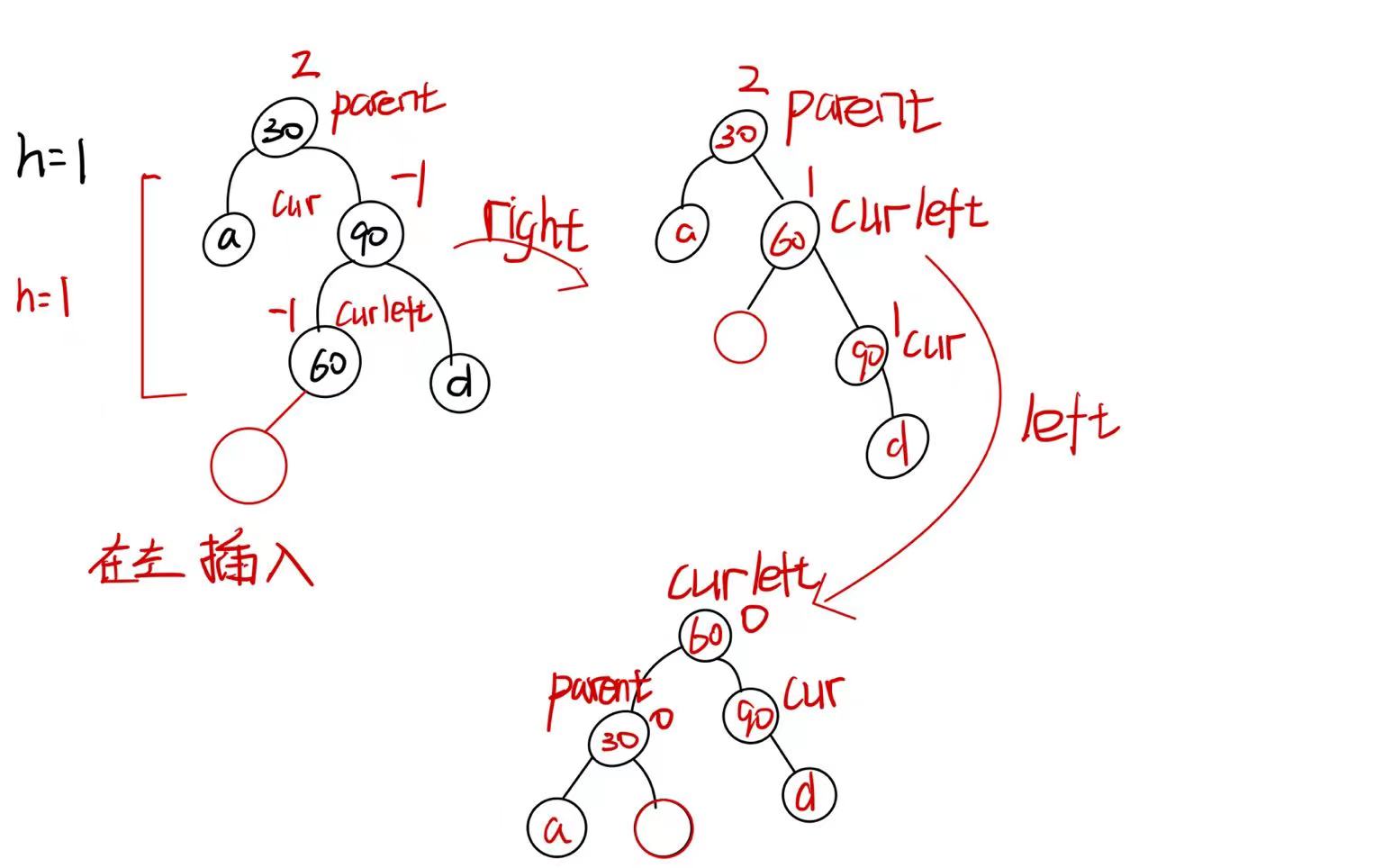
1cc1e4b1c03dfbb74949479a83b359e

旋转完成后,parent->bf=0 cur->bf=1 curleft->bf=0

在右边插入(curleft->bf==1)

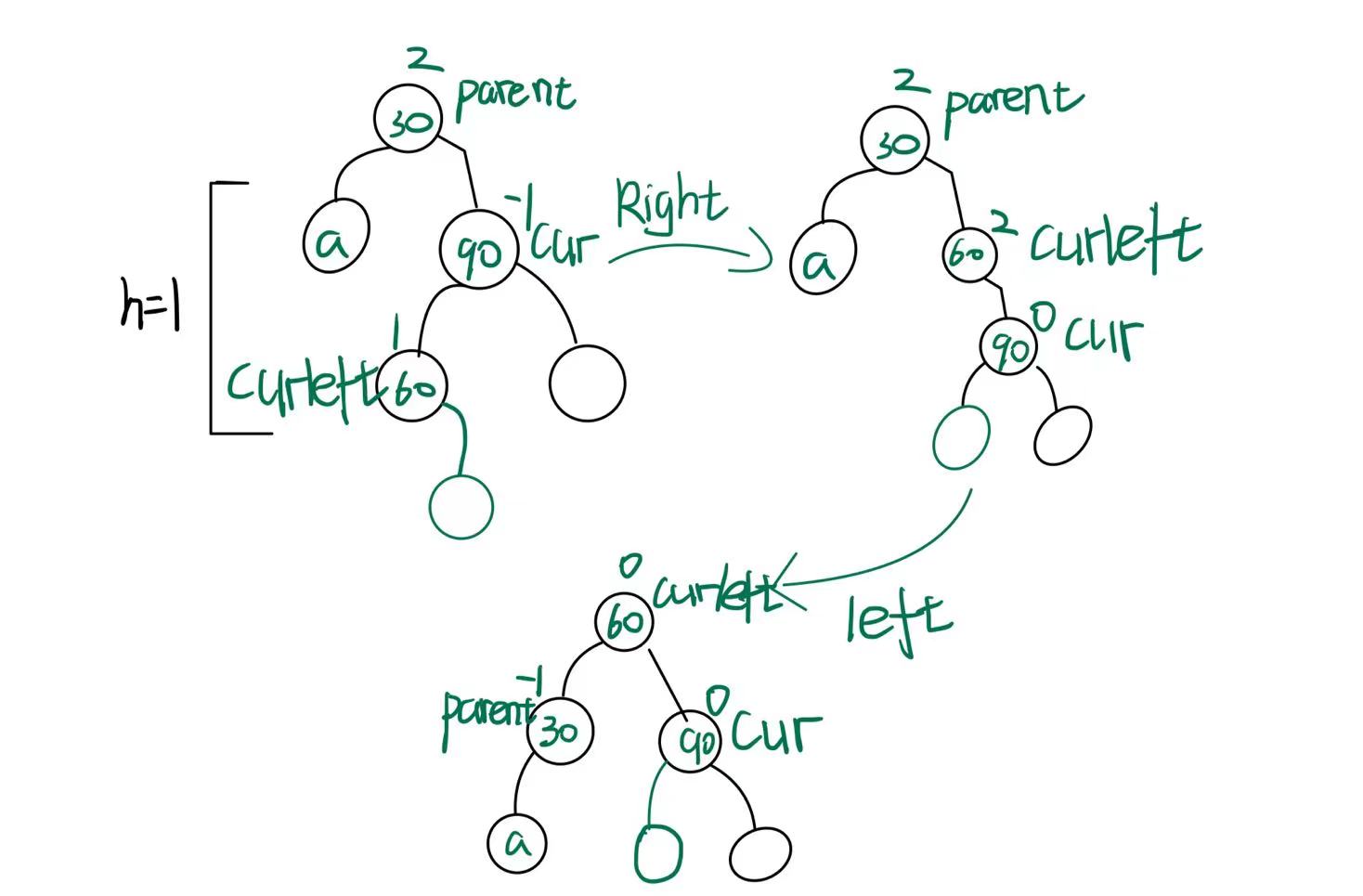
27bd9f72cfc3de5bd1d4600090a200b

旋转完成后,parent->bf=-1 cur->bf=0 curleft->bf=0

当h==2时,此时也可以分为在左边插入以及在右边插入

在左边插入(curleft->bf==-1)

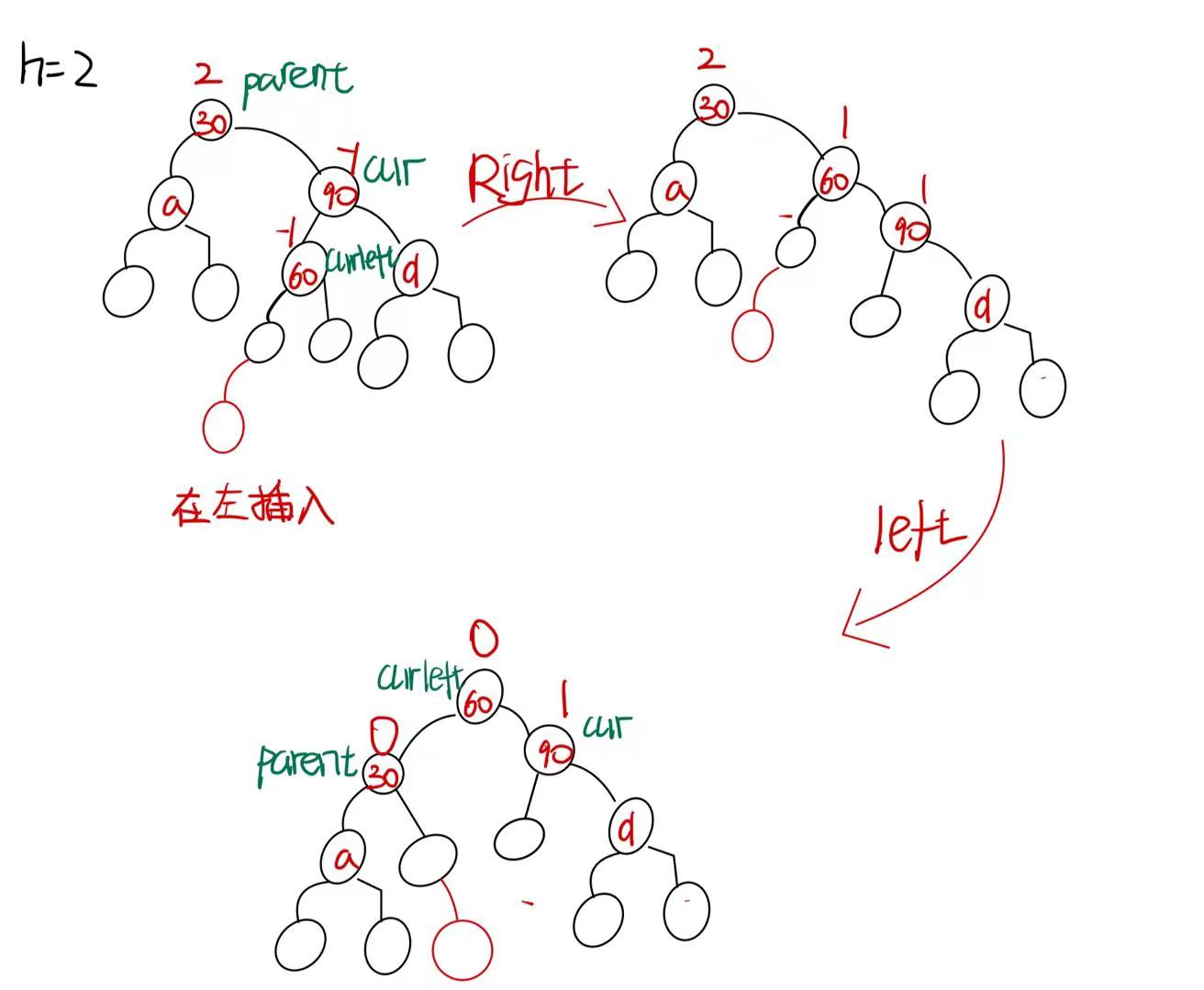
旋转完成后,parent->bf=0 cur->bf=1 curleft->bf=0

在右边插入(curleft->bf==1)

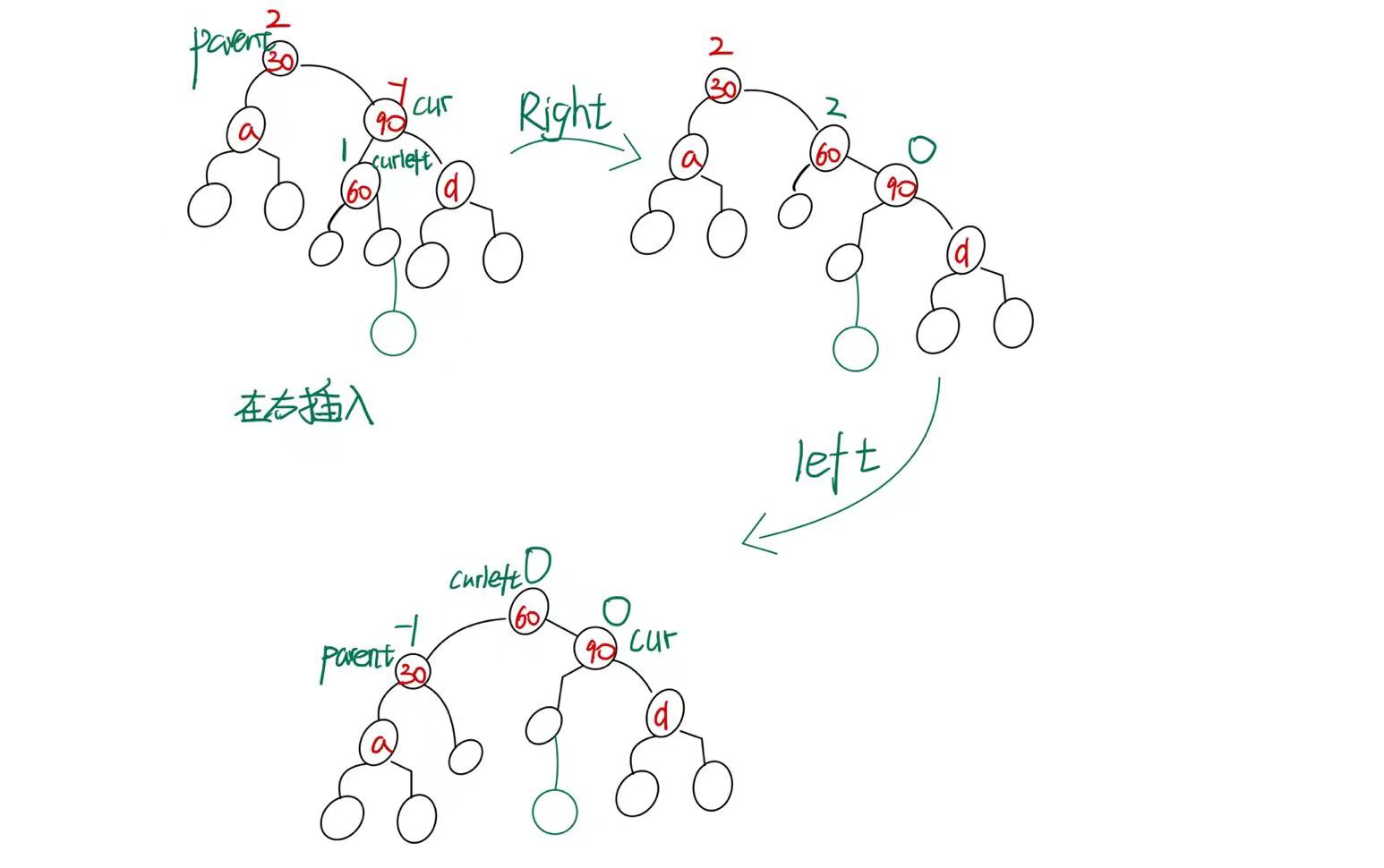
02483a63e12eca2b1a06d74d751ac62

旋转完成后,parent->bf=-1 cur->bf=0 curleft->bf=0

可以看出,引发右左双旋的原因为:cur->bf==-1,parent->bf==2

所以其代码可以复用之前的旋转,但之前的旋转改变了平衡因子,我们需要依照上面的规律再特殊处理一下

void RotaRL(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateR(parent);RotateL(parent->_left);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}if (bf == -1){parent->_bf = 0;cur->_bf = 1;curright->_bf = 0;}if (bf == 1){parent->_bf = -1;cur->_bf = 0;curright->_bf = 0;}
}

2.4 左右双旋

其抽象模型为:

ea71377250854e9e30ddcce8fc42f3b

这个模型实在有点抽象,我们分以下几种情况来讨论.

h0 此时60为插入的节点(curright->bf0)

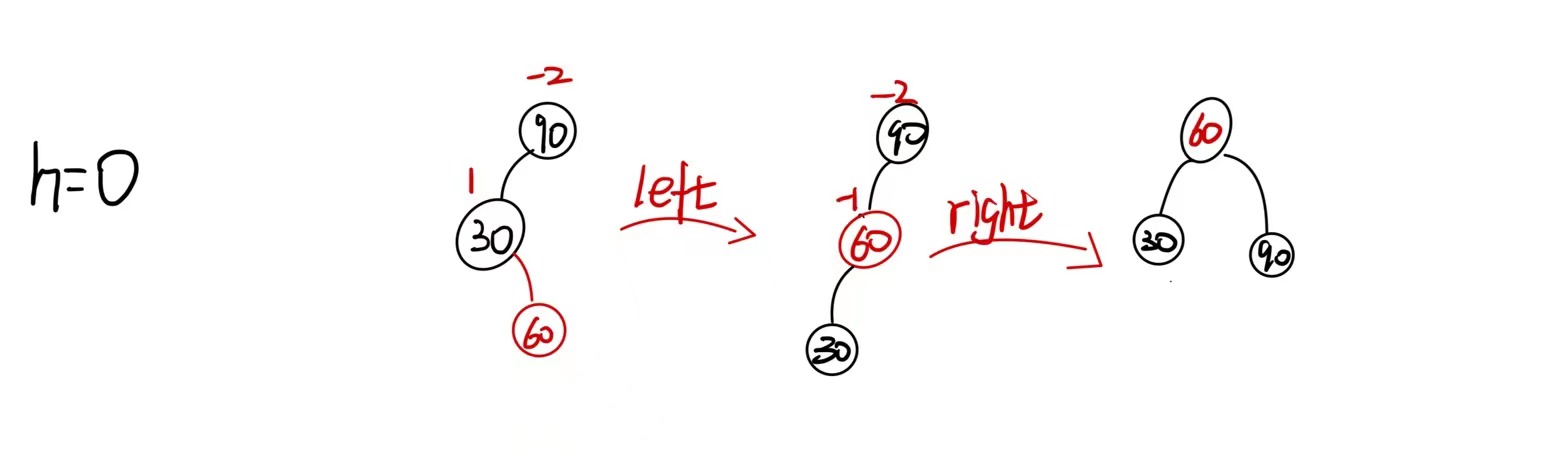
d30d04a914ff74ea0017aadfec25d01

旋转完成后,parent->bf=cur->bf=curright->bf=0

当h==1时,此时可以分为在60的左边插入或者在60的右边插入

在左边插入(curright->bf==-1)

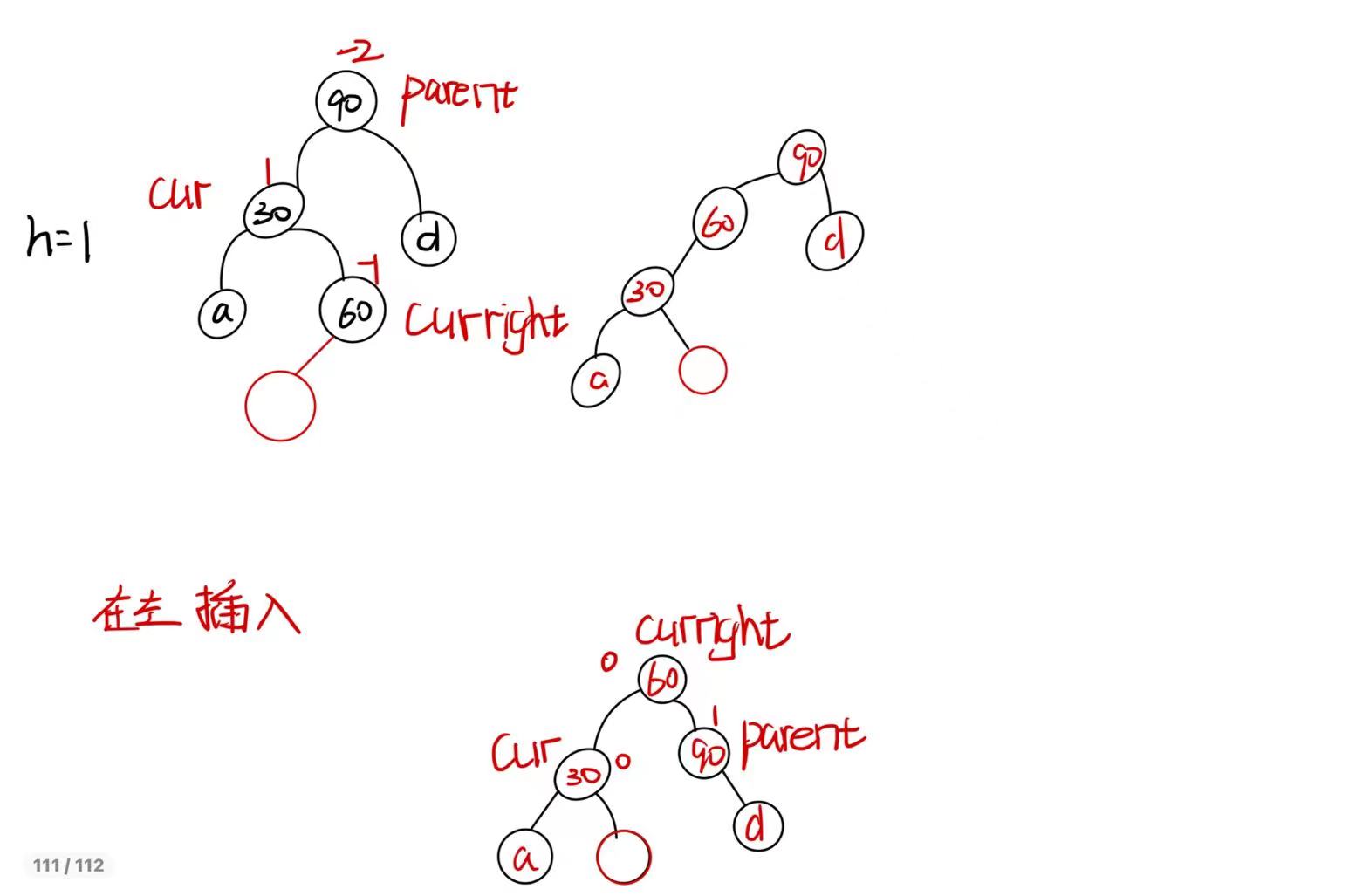
e0bd4568684f60c958743920758317e

旋转完成后,parent->bf=1 cur->bf=0 curleft->bf=0

在右边插入(curright->bf==1)

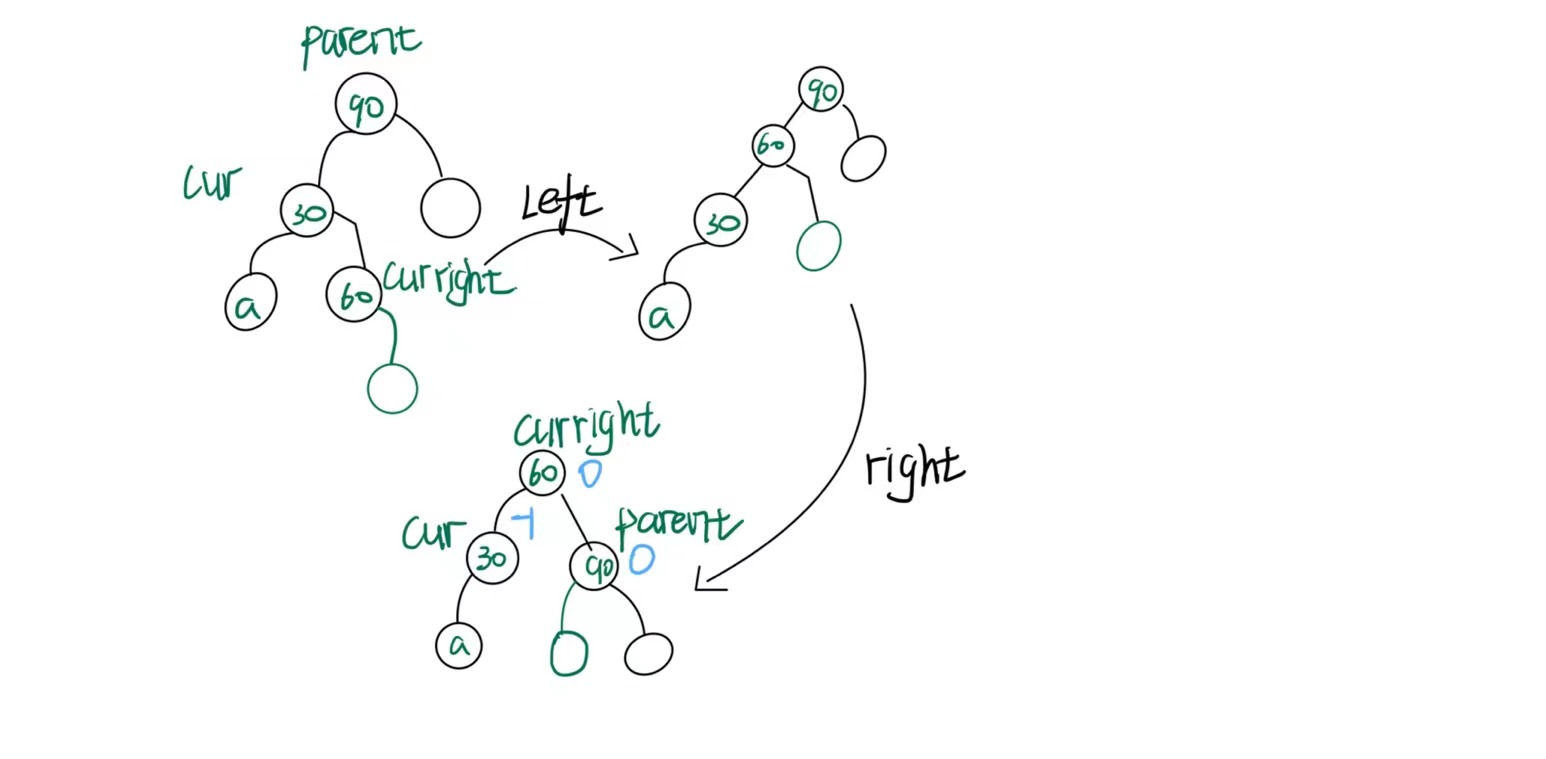
960b1d4215886847c0cebaf7d0d44ce

旋转完成后,parent->bf=0 cur->bf=-1 curright->bf=0

当h==2时,此时也可以分为在左边插入以及在右边插入

在左边插入(curright->bf==-1)

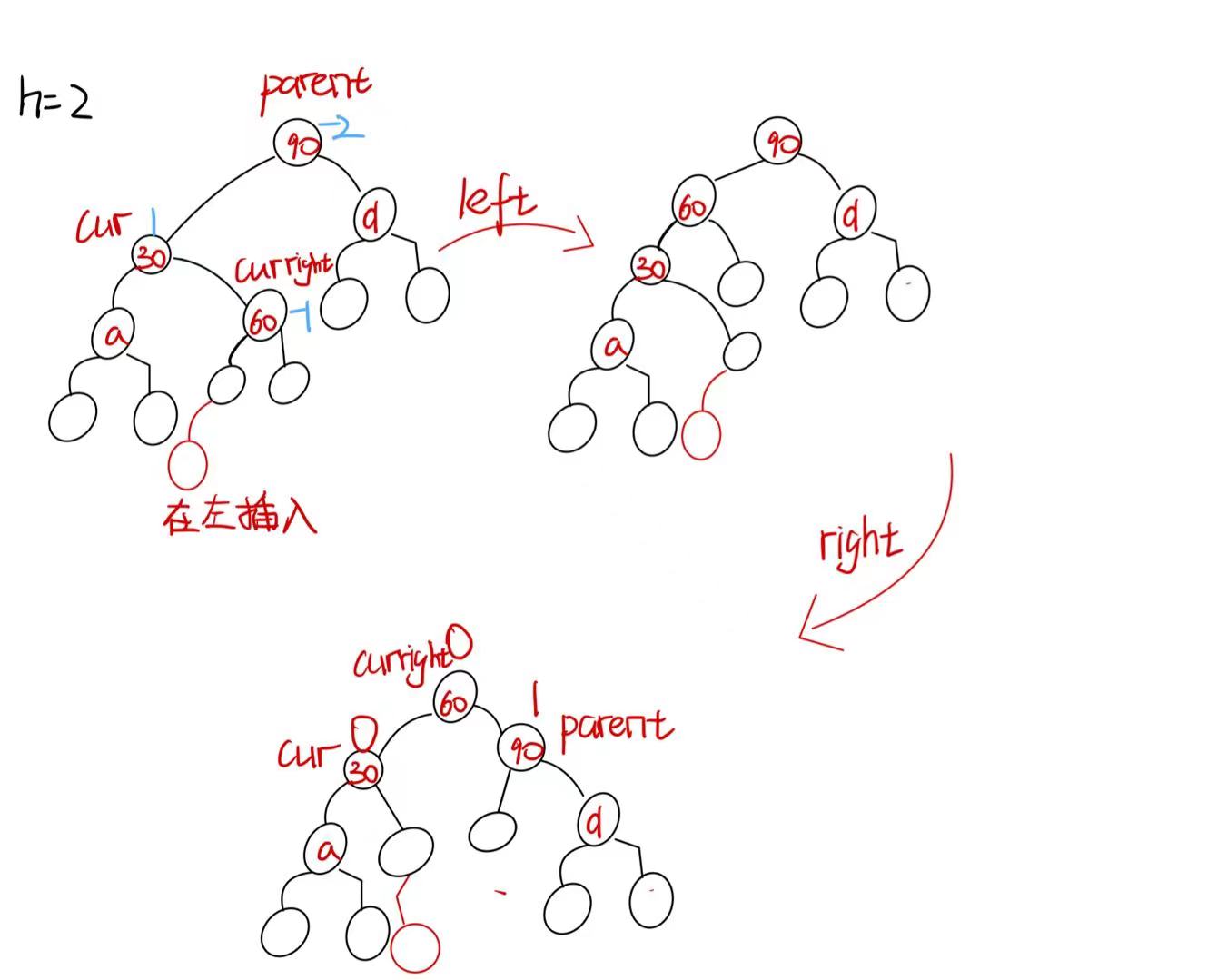
旋转完成后,parent->bf=1 cur->bf=0 curright->bf=0

在右边插入(60->bf==1)

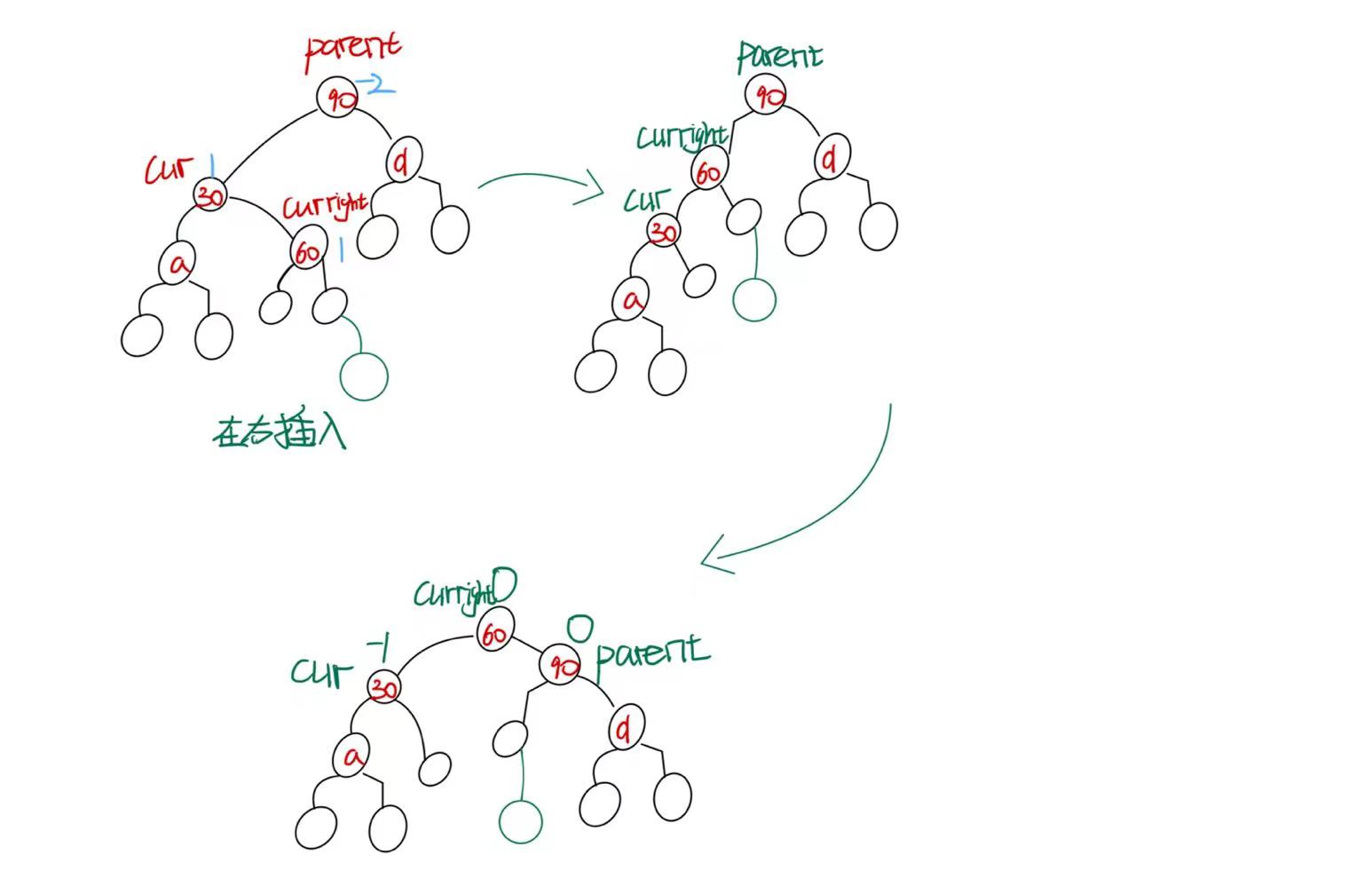
79eeeda5389aad2f9cd95dbc7796ccb

旋转完成后,parent->bf=0 cur->bf=-1 curright->bf=0

可以看出,引发左右双旋的原因为:cur->bf1,parent->bf-2

void RotaLR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->right;int bf = curright->_bf;RotateL(cur);RotateR(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}
}

3. 旋转判定

旋转的判定为:同号单旋,异号双旋(将cur旋转为parent同号)

if (parent->_bf == -2 || parent->_bf == 2)
{if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotaRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotaLR(parent);}break;
}

4. 验证是否为AVL树

bool IsAVLTree()
{return IsAVLTree(_root);
}
bool IsAVLTree(Node* root)
{if (root == nullptr)return true;int leftheight = Height(root->_left);int rightheight= Height(root->_right);if (rightheight - leftheight != root->_bf){cout << "异常" << rightheight<< " " << leftheight<< " "<<root->_bf<<endl;return false;}return abs(rightheight - leftheight) < 2 && IsAVLTree(root->_left) && IsAVLTree(root->_right);
}
int Height(Node* root)
{if (root == nullptr)return 0;int leftheight = Height(root->_left);int rightheight = Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}

5.完整源码(AVL插入旋转)

#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
template<typename K,typename V>
struct TreeNode
{	pair<K, V>_val;TreeNode<K,V>* _left;TreeNode<K,V>* _right;TreeNode<K,V>* _parent;int _bf;TreeNode(const pair<K,V> val):_val(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
template<typename K,typename V>
class AVLBSTree {typedef TreeNode<K,V> Node;
public:bool Insert(const pair<K, V> kv){Node* parent = _root;Node* cur = _root;if (_root == nullptr){_root = new Node(kv);return true;}while (cur){if (kv.first > cur->_val.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_val.first){parent = cur;cur = cur->_left;}else return false;;}cur = new Node(kv);if (parent->_val.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else parent->_bf++;if (parent->_bf == 0)break;else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotaRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotaLR(parent);}break;}else assert(false);}     return true;}void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;if (curleft)curleft->_parent = parent;parent->_right = curleft;cur->_left = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (_root == parent){cur->_parent = nullptr;_root = cur;}else{if (pparent->_left == parent){pparent->_left = cur;}else pparent->_right = cur;cur->_parent = pparent;}parent->_bf =cur->_bf= 0;}void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;if (curright){curright->_parent = parent;}parent->_left = curright;cur->_right = parent;if (parent == _root){cur->_left = parent;}else{Node* pparent = parent->_parent;if (pparent->_left == parent){pparent->_left = cur;}elsepparent->_right = cur;cur->_parent = pparent;}parent->_bf = cur->_bf = 0;parent->_parent = cur;}void RotaRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curleft->_bf = 0;}if (bf == -1){parent->_bf = 0;cur->_bf = 1;curleft->_bf = 0;}if (bf == 1){parent->_bf = -1;cur->_bf = 0;curleft->_bf = 0;}}void RotaLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(cur);RotateR(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}}bool IsAVLTree(){return IsAVLTree(_root);}bool IsAVLTree(Node* root){if (root == nullptr)return true;int leftheight = Height(root->_left);int rightheight= Height(root->_right);if (rightheight - leftheight != root->_bf){cout << "异常" << rightheight<< " " << leftheight<< " "<<root->_bf<<endl;return false;}return abs(rightheight - leftheight) < 2 && IsAVLTree(root->_left) && IsAVLTree(root->_right);}int Height(Node* root){if (root == nullptr)return 0;int leftheight = Height(root->_left);int rightheight = Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}
private:Node* _root = nullptr;
};