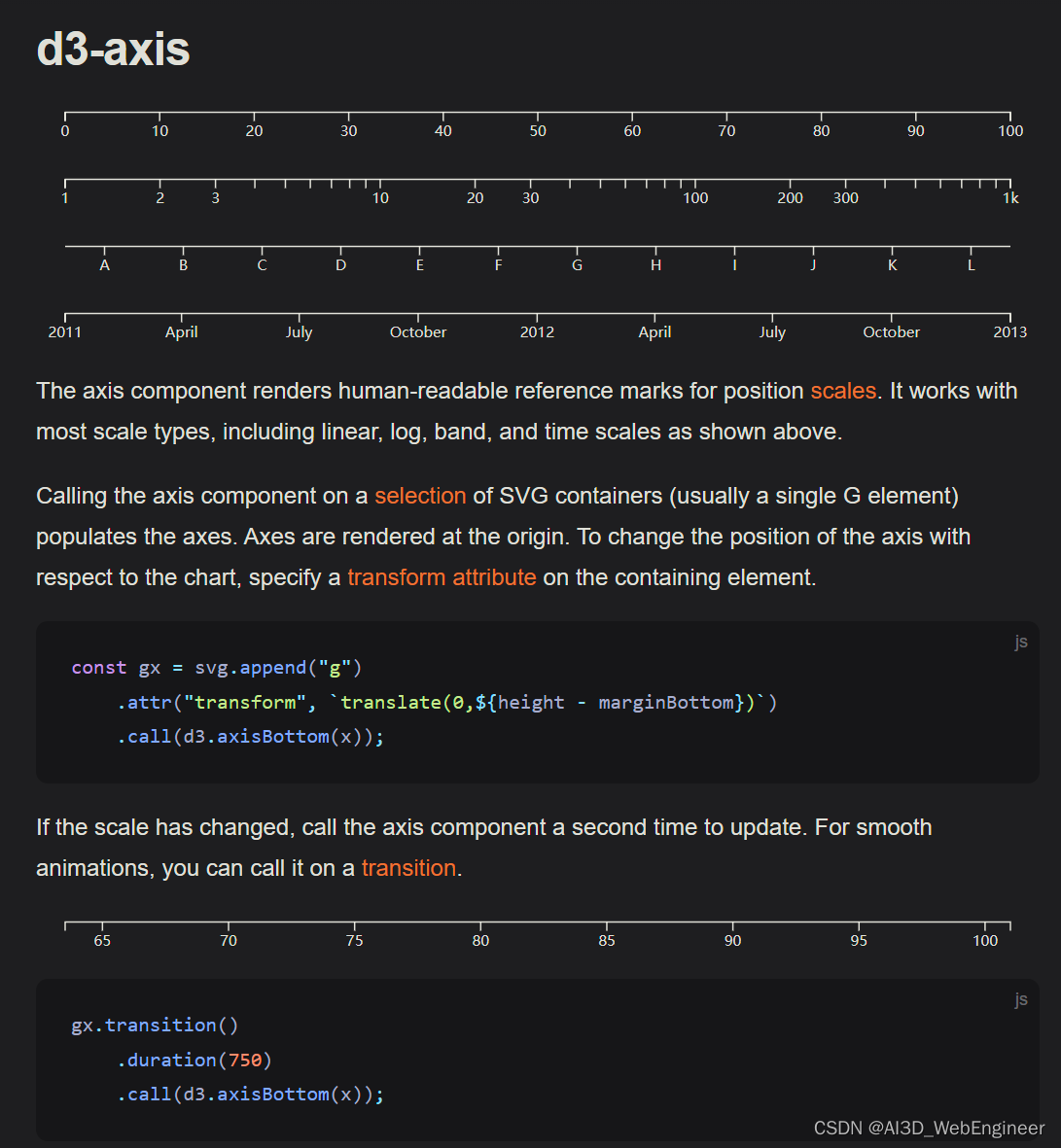
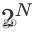一、可见性验证

下面的程序验证了voliate的可见性。

public class VolatileVisibilityTest {private static volatile boolean inintFlag = false;public static void main(String[] args) throws InterruptedException {new Thread(() -> {System.out.println("waiting data...");while (!inintFlag){}System.out.println("===============success");}).start();Thread.sleep(2000);new Thread(() -> prepareData()).start();}public static void prepareData(){System.out.println("prepare data.....");inintFlag = true;System.out.println("prepare data end....");}
}

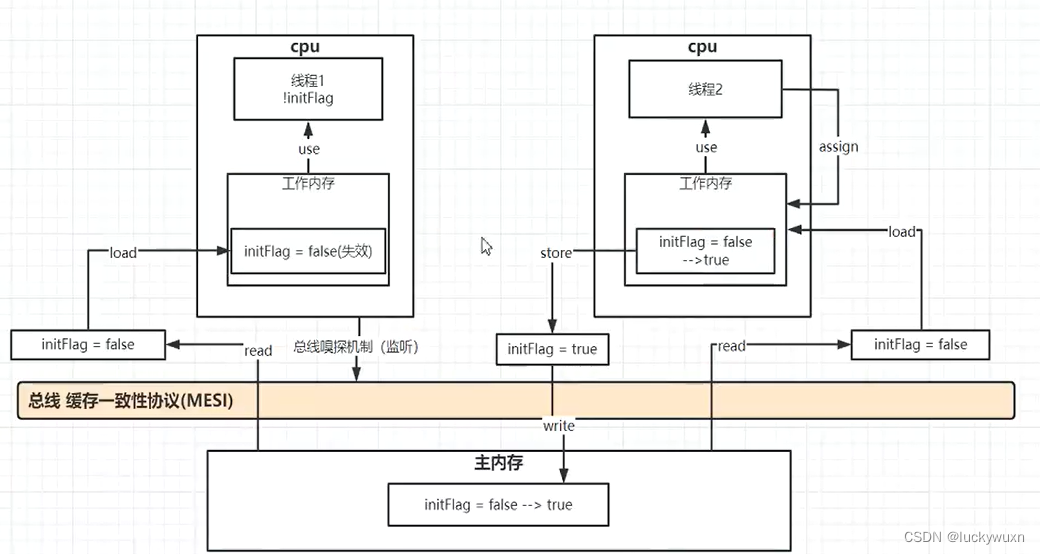
代码执行过程如下：

• voliate可见性的底层实现原理
  通过程序执行的汇编指令发现，是通过锁机制实现的。

验证过程

• 下载反汇编程序插件
  下载地址：https://download.csdn.net/download/luckywuxn/88347740
• 插件配置
  将hsdis-amd64.dll放在 $JAVA_HOME/jre/bin/server 目录下
• idea中设置启动参数
  -server -Xcomp -XX:+UnlockDiagnosticVMOptions -XX:+PrintAssembly -XX:CompileCommand=compileonly,*VolitaleDemo.main
• 启动程序查看结果
  控制台搜索lock关键字，将看到如下结果，结果现在lock指令执行的程序是在源代码的第28行。
  

二、有序性

• 示例一

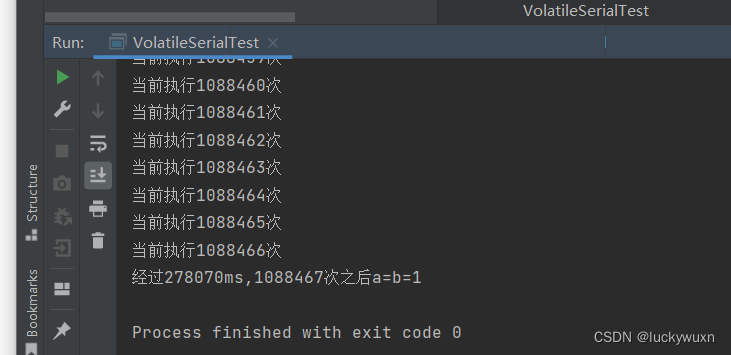
public class VolatileSerialTest {static int x = 0,y = 0;static int a = 0,b = 0;public static void main(String[] args) throws InterruptedException {long startTime = System.currentTimeMillis();for (int i = 0;; i ++){x = 0;y = 0;a = 0;b = 0;Thread one = new Thread(() -> {a = y;x = 1;});Thread other = new Thread(() -> {b = x;y = 1;});one.start();other.start();one.join();other.join();if (a == 1 && b == 1){long endTime = System.currentTimeMillis();System.out.println("经过" + (endTime - startTime) + "ms," + i + "次之后a=b=1");break;}System.out.println("当前执行" + i + "次");}}
}

运行上面代码，得到以下结果，由此我们可以得到结论，在没有使用voliate关键字时，两个线程中的两条指令是可以重排序的。

• 示例二

public class VolatileSerialTest2 {private static VolatileSerialTest2 instance = null;private VolatileSerialTest2(){}public static VolatileSerialTest2 getInstance(){if (instance == null){synchronized (VolatileSerialTest2.class){if (instance == null){instance = new VolatileSerialTest2();}}}return instance;}public static void main(String[] args) {VolatileSerialTest2 instance = VolatileSerialTest2.getInstance();}}

编译之后，通过idea插件jclasslib插件可以看到字节码文件如下

由JMM规范可知，如果第11、12行是最新as-if-serial & happens-before 原则的，所有这两条指令是可能重排序的，为了防止重排序，我们只需要加上voliate关键字就可以了。

三、原子性验证

下面是一个原子性验证的代码：

class Counter {private volatile int count = 0;public void increment() {count++;}public int getCount() {return count;}
}public class VolatileAtomicTest {public static void main(String[] args) {final Counter counter = new Counter();// 创建两个线程，同时递增计数器的值Thread thread1 = new Thread(() -> {for (int i = 0; i < 1000; i++) {counter.increment();}});Thread thread2 = new Thread(() -> {for (int i = 0; i < 1000; i++) {counter.increment();}});thread1.start();thread2.start();// 等待两个线程执行完成try {thread1.join();thread2.join();} catch (InterruptedException e) {e.printStackTrace();}// 输出最终的计数器值System.out.println("Final Count: " + counter.getCount());}
}

运行上面代码，结果如下

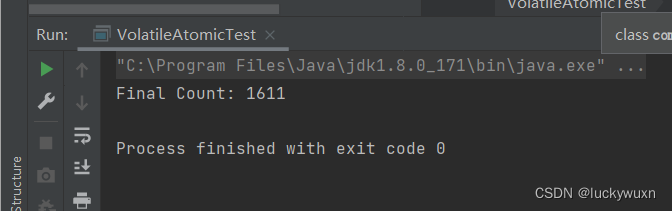
上面程序使用两个线程同时对voliate修饰的变量count进行累计操作，voliate对所有线程都是可见的，那为什么结果不是2000呢，这是由于voliate修饰的变量并不是原子的。