深度学习模型一般由各种模型层组合而成。
torch.nn中内置了非常丰富的各种模型层。它们都属于nn.Module的子类，具备参数管理功能。
例如：
nn.Linear, nn.Flatten, nn.Dropout, nn.BatchNorm2d, nn.Embedding
nn.Conv2d,nn.AvgPool2d,nn.Conv1d,nn.ConvTranspose2d
nn.GRU,nn.LSTM
nn.Transformer
如果这些内置模型层不能够满足需求，我们也可以通过继承nn.Module基类构建自定义的模型层。
实际上，pytorch不区分模型和模型层，都是通过继承nn.Module进行构建。
因此，我们只要继承nn.Module基类并实现forward方法即可自定义模型层。

一、基础层

一些基础的内置模型层简单介绍如下。

• nn.Linear：全连接层。参数个数 = 输入层特征数× 输出层特征数(weight)＋ 输出层特征数(bias)
• nn.Embedding：嵌入层。一种比Onehot更加有效的对离散特征进行编码的方法。**一般用于将输入中的单词映射为稠密向量。**嵌入层的参数需要学习。
• nn.Flatten：压平层，用于将多维张量样本压成一维张量样本。
• nn.BatchNorm1d：一维批标准化层。通过线性变换将输入批次缩放平移到稳定的均值和标准差。可以增强模型对输入不同分布的适应性，加快模型训练速度，有轻微正则化效果。一般在激活函数之前使用。可以用afine参数设置该层是否含有可以训练的参数。
• nn.BatchNorm2d：二维批标准化层。 常用于CV领域。
• nn.BatchNorm3d：三维批标准化层。
• nn.Dropout：一维随机丢弃层。一种正则化手段。
• nn.Dropout2d：二维随机丢弃层。
• nn.Dropout3d：三维随机丢弃层。
• nn.Threshold：限幅层。当输入大于或小于阈值范围时，截断之。
• nn.ConstantPad2d： 二维常数填充层。对二维张量样本填充常数扩展长度。
• nn.ReplicationPad1d： 一维复制填充层。对一维张量样本通过复制边缘值填充扩展长度。
• nn.ZeroPad2d：二维零值填充层。对二维张量样本在边缘填充0值.
• nn.GroupNorm：组归一化。一种替代批归一化的方法，将通道分成若干组进行归一。不受batch大小限制。
• nn.LayerNorm：层归一化。常用于NLP领域，不受序列长度不一致影响。
• nn.InstanceNorm2d: 样本归一化。一般在图像风格迁移任务中效果较好。

重点说说各种归一化层：

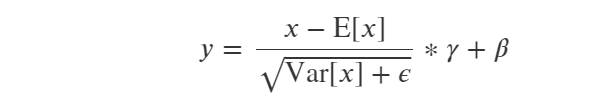
结构化数据的BatchNorm1D归一化 【结构化数据的主要区分度来自每个样本特征在全体样本中的排序，将全部样本的某个特征都进行相同的放大缩小平移操作，样本间的区分度基本保持不变，所以结构化数据可以做BatchNorm，但LayerNorm会打乱全体样本根据某个特征的排序关系，引起区分度下降】

图片数据的各种归一化(一般常用BatchNorm2D)【图片数据的主要区分度来自图片中的纹理结构，所以图片数据的归一化一定要在图片的宽高方向上操作以保持纹理结构，此外在Batch维度上操作还能够引入少许的正则化，对提升精度有进一步的帮助。】

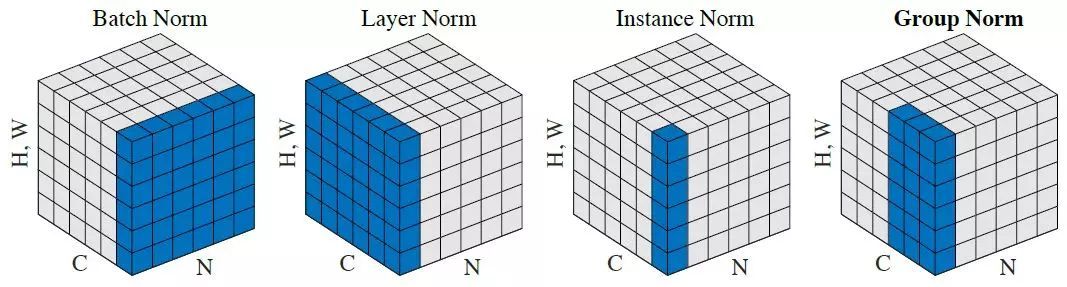
文本数据的LayerNorm归一化 【文本数据的主要区分度来自于词向量(Embedding向量)的方向，所以文本数据的归一化一定要在 特征(通道)维度上操作 以保持 词向量方向不变。此外文本数据还有一个重要的特点是不同样本的序列长度往往不一样，所以不可以在Sequence和Batch维度上做归一化，否则将不可避免地让padding位置对应的向量变成非零向量】

此外，有论文提出了一种可自适应学习的归一化：SwitchableNorm，可应用于各种场景且有一定的效果提升。【SwitchableNorm是将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。】论文链接
对BatchNorm需要注意的几点：
(1)BatchNorm放在激活函数前还是激活函数后？
原始论文认为将BatchNorm放在激活函数前效果较好，后面的研究一般认为将BatchNorm放在激活函数之后更好。
(2)BatchNorm在训练过程和推理过程的逻辑是否一样？
不一样！训练过程BatchNorm的均值和方差和根据mini-batch中的数据估计的，而推理过程中BatchNorm的均值和方差是用的训练过程中的全体样本估计的。因此预测过程是稳定的，相同的样本不会因为所在批次的差异得到不同的结果，但训练过程中则会受到批次中其他样本的影响所以有正则化效果。
(3)BatchNorm的精度效果与batch_size大小有何关系?
如果受到GPU内存限制，不得不使用很小的batch_size，训练阶段时使用的mini-batch上的均值和方差的估计和预测阶段时使用的全体样本上的均值和方差的估计差异可能会较大，效果会变差。这时候，可以尝试LayerNorm或者GroupNorm等归一化方法。

nn.BatchNorm2d：

import torch 
from torch import nn batch_size, channel, height, width = 32, 16, 128, 128tensor = torch.arange(0,32*16*128*128).view(32,16,128,128).float() bn = nn.BatchNorm2d(num_features=channel,affine=False)
bn_out = bn(tensor)channel_mean = torch.mean(bn_out[:,0,:,:]) 
channel_std = torch.std(bn_out[:,0,:,:])
print("channel mean:",channel_mean.item())
print("channel std:",channel_std.item())

nn.LayerNorm：

import torch 
from torch import nn batch_size, sequence, features = 32, 100, 2048
tensor = torch.arange(0,32*100*2048).view(32,100,2048).float() ln = nn.LayerNorm(normalized_shape=[features],elementwise_affine = False)ln_out = ln(tensor)token_mean = torch.mean(ln_out[0,0,:]) 
token_std = torch.std(ln_out[0,0,:])
print("token_mean:",token_mean.item())
print("token_mean:",token_std.item())

二、卷积网络相关层

一些与卷积相关的内置层介绍如下：
nn.Conv1d：普通一维卷积，常用于文本。参数个数 = 输入通道数×卷积核尺寸(如3)×卷积核个数 + 卷积核尺寸(如3）=卷积核尺寸(如3乘3)x输出通道数+输出通道数（偏置数量）
nn.Conv2d：普通二维卷积，常用于图像。参数个数 = 输入通道数×卷积核尺寸(如3乘3)×卷积核个数 + 卷积核尺寸(如3乘3)。=卷积核尺寸(如3乘3)x输入通道数x输出通道数+输出通道数（偏置数量）) 通过调整dilation参数大于1，可以变成空洞卷积，增加感受野。 通过调整groups参数不为1，可以变成分组卷积。分组卷积中每个卷积核仅对其对应的一个分组进行操作。 当groups参数数量等于输入通道数时，相当于tensorflow中的二维深度卷积层tf.keras.layers.DepthwiseConv2D。 利用分组卷积和1乘1卷积的组合操作，可以构造相当于Keras中的二维深度可分离卷积层tf.keras.layers.SeparableConv2D。
nn.Conv3d：普通三维卷积，常用于视频。参数个数 = 输入通道数×卷积核尺寸(如3乘3乘3)×卷积核个数 + 卷积核尺寸(如3乘3乘3) 。
nn.MaxPool1d: 一维最大池化。
nn.MaxPool2d：二维最大池化。一种下采样方式。没有需要训练的参数。
nn.MaxPool3d：三维最大池化。
nn.AdaptiveMaxPool2d：二维自适应最大池化。无论输入图像的尺寸如何变化，输出的图像尺寸是固定的。 该函数的实现原理，大概是通过输入图像的尺寸和要得到的输出图像的尺寸来反向推算池化算子的padding,stride等参数。
nn.FractionalMaxPool2d：二维分数最大池化。普通最大池化通常输入尺寸是输出的整数倍。而分数最大池化则可以不必是整数。分数最大池化使用了一些随机采样策略，有一定的正则效果，可以用它来代替普通最大池化和Dropout层。
nn.AvgPool2d：二维平均池化。
nn.AdaptiveAvgPool2d：二维自适应平均池化。无论输入的维度如何变化，输出的维度是固定的。
nn.ConvTranspose2d：二维卷积转置层，俗称反卷积层。并非卷积的逆操作，但在卷积核相同的情况下，当其输入尺寸是卷积操作输出尺寸的情况下，卷积转置的输出尺寸恰好是卷积操作的输入尺寸。在语义分割中可用于上采样。
nn.Upsample：上采样层，操作效果和池化相反。可以通过mode参数控制上采样策略为"nearest"最邻近策略或"linear"线性插值策略。
nn.Unfold：滑动窗口提取层。其参数和卷积操作nn.Conv2d相同。实际上，卷积操作可以等价于nn.Unfold和nn.Linear以及nn.Fold的一个组合。 其中nn.Unfold操作可以从输入中提取各个滑动窗口的数值矩阵，并将其压平成一维。利用nn.Linear将nn.Unfold的输出和卷积核做乘法后，再使用 nn.Fold操作将结果转换成输出图片形状。
nn.Fold：逆滑动窗口提取层。

重点说说各种常用的卷积层和上采样层：
普通卷积【普通卷积的操作分成3个维度，在空间维度(H和W维度)是共享卷积核权重滑窗相乘求和(融合空间信息)，在输入通道维度是每一个通道使用不同的卷积核参数并对输入通道维度求和(融合通道信息)，在输出通道维度操作方式是并行堆叠(多种)，有多少个卷积核就有多少个输出通道】

空洞卷积【和普通卷积相比，空洞卷积可以在保持较小参数规模的条件下增大感受野，常用于图像分割领域。其缺点是可能产生网格效应，即有些像素被空洞漏过无法利用到，可以通过使用不同膨胀因子的空洞卷积的组合来克服该问题。

分组卷积 【和普通卷积相比，分组卷积将输入通道分成g组，卷积核也分成对应的g组，每个卷积核只在其对应的那组输入通道上做卷积，最后将g组结果堆叠拼接。由于每个卷积核只需要在全部输入通道的1/g个通道上做卷积，参数量降低为普通卷积的1/g。分组卷积要求输入通道和输出通道数都是g的整数倍。

深度可分离卷积【深度可分离卷积的思想是先用g=m(输入通道数)的分组卷积逐通道作用融合空间信息，再用n(输出通道数)个1乘1卷积融合通道信息。 其参数量为 (m×k×k)+ n×m, 相比普通卷积的参数量 m×n×k×k 显著减小 】。

转置卷积 【一般的卷积操作后会让特征图尺寸变小，但转置卷积(也被称为反卷积)可以实现相反的效果，即放大特征图尺寸。对两种方式理解转置卷积，第一种方式是转置卷积是一种特殊的卷积，通过设置合适的padding的大小来恢复特征图尺寸。第二种理解基于卷积运算的矩阵乘法表示方法，转置卷积相当于将卷积核对应的表示矩阵做转置，然后乘上输出特征图压平的一维向量，即可恢复原始输入特征图的大小。

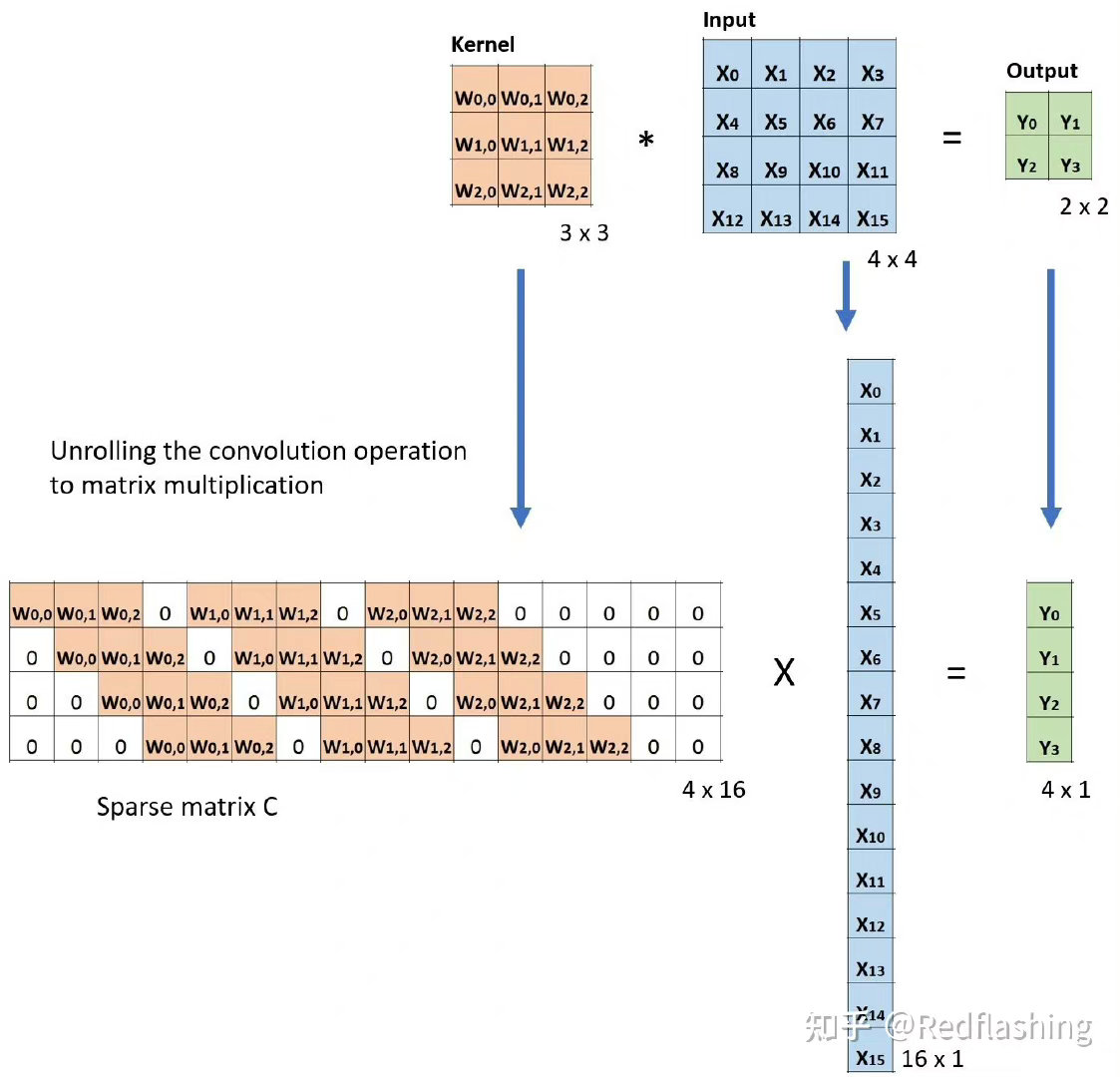
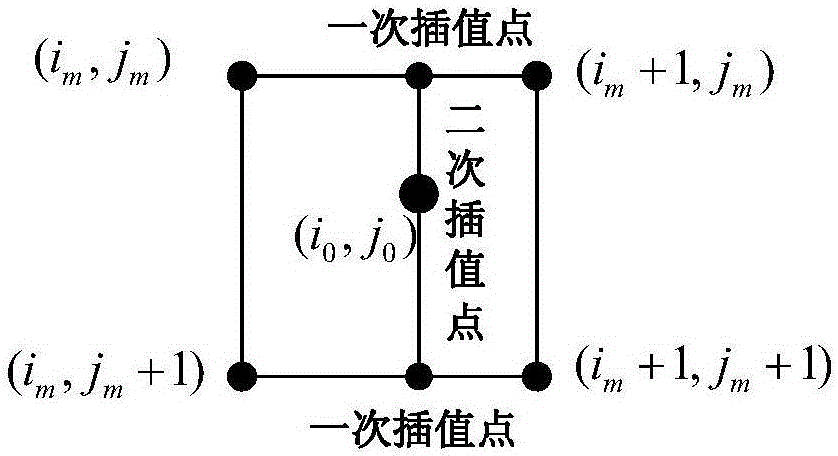
上采样层 【除了使用转置卷积进行上采样外，在图像分割领域更多的时候一般是使用双线性插值的方式进行上采样，该方法没有需要学习的参数，通常效果也更好，除了双线性插值之外，还可以使用最邻近插值的方式进行上采样，但使用较少。】

import torch 
from torch import nn 
import torch.nn.functional as F # 卷积输出尺寸计算公式 o = (i + 2*p -k')//s  + 1 
# 对空洞卷积 k' = d(k-1) + 1
# o是输出尺寸，i 是输入尺寸，p是 padding大小， k 是卷积核尺寸， s是stride步长, d是dilation空洞参数inputs = torch.arange(0,25).view(1,1,5,5).float() # i= 5
filters = torch.tensor([[[[1.0,1],[1,1]]]]) # k = 2outputs = F.conv2d(inputs, filters) # o = (5+2*0-2)//1+1 = 4
outputs_s2 = F.conv2d(inputs, filters, stride=2)  #o = (5+2*0-2)//2+1 = 2
outputs_p1 = F.conv2d(inputs, filters, padding=1) #o = (5+2*1-2)//1+1 = 6
outputs_d2 = F.conv2d(inputs,filters, dilation=2) #o = (5+2*0-(2(2-1)+1))//1+1 = 3print("--inputs--")
print(inputs)
print("--filters--")
print(filters)print("--outputs--")
print(outputs,"\n")print("--outputs(stride=2)--")
print(outputs_s2,"\n")print("--outputs(padding=1)--")
print(outputs_p1,"\n")print("--outputs(dilation=2)--")
print(outputs_d2,"\n")

import torch 
from torch import nn features = torch.randn(8,64,128,128)
print("features.shape:",features.shape)
print("\n")#普通卷积
print("--conv--")
conv = nn.Conv2d(in_channels=64,out_channels=32,kernel_size=3)
conv_out = conv(features)
print("conv_out.shape:",conv_out.shape) 
print("conv.weight.shape:",conv.weight.shape)
print("\n")#分组卷积
print("--group conv--")
conv_group = nn.Conv2d(in_channels=64,out_channels=32,kernel_size=3,groups=8)
group_out = conv_group(features)
print("group_out.shape:",group_out.shape) 
print("conv_group.weight.shape:",conv_group.weight.shape)
print("\n")#深度可分离卷积
print("--separable conv--")
depth_conv = nn.Conv2d(in_channels=64,out_channels=64,kernel_size=3,groups=64)
oneone_conv = nn.Conv2d(in_channels=64,out_channels=32,kernel_size=1)
separable_conv = nn.Sequential(depth_conv,oneone_conv)
separable_out = separable_conv(features)
print("separable_out.shape:",separable_out.shape) 
print("depth_conv.weight.shape:",depth_conv.weight.shape)
print("oneone_conv.weight.shape:",oneone_conv.weight.shape)
print("\n")#转置卷积
print("--conv transpose--")
conv_t = nn.ConvTranspose2d(in_channels=32,out_channels=64,kernel_size=3)
features_like = conv_t(conv_out)
print("features_like.shape:",features_like.shape)
print("conv_t.weight.shape:",conv_t.weight.shape)

import torch 
from torch import nn inputs = torch.arange(1, 5, dtype=torch.float32).view(1, 1, 2, 2)
print("inputs:")
print(inputs)
print("\n")
# 上采样
nearest = nn.Upsample(scale_factor=2, mode='nearest')
bilinear = nn.Upsample(scale_factor=2,mode="bilinear",align_corners=True)print("nearest(inputs)：")
print(nearest(inputs))
print("\n")
print("bilinear(inputs)：")
print(bilinear(inputs)) 

三、循环网络相关层

nn.LSTM：长短记忆循环网络层【支持多层】。最普遍使用的循环网络层。具有携带轨道，遗忘门，更新门，输出门。可以较为有效地缓解梯度消失问题，从而能够适用长期依赖问题。设置bidirectional = True时可以得到双向LSTM。需要注意的时，默认的输入和输出形状是(seq,batch,feature), 如果需要将batch维度放在第0维，则要设置batch_first参数设置为True。
nn.GRU：门控循环网络层【支持多层】。LSTM的低配版，不具有携带轨道，参数数量少于LSTM，训练速度更快。
nn.RNN：简单循环网络层【支持多层】。容易存在梯度消失，不能够适用长期依赖问题。一般较少使用。
nn.LSTMCell：长短记忆循环网络单元。和nn.LSTM在整个序列上迭代相比，它仅在序列上迭代一步。一般较少使用。
nn.GRUCell：门控循环网络单元。和nn.GRU在整个序列上迭代相比，它仅在序列上迭代一步。一般较少使用。
nn.RNNCell：简单循环网络单元。和nn.RNN在整个序列上迭代相比，它仅在序列上迭代一步。一般较少使用。
一般地，各种RNN序列模型层(RNN,GRU,LSTM等)可以用函数表示如下:

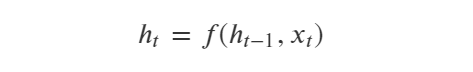
这个公式的含义是：t时刻循环神经网络的输出向量ℎ𝑡由t-1时刻的输出向量ℎ𝑡−1和t时刻的输入𝑖𝑡变换而来。

• LSTM结构解析：

LSTM通过引入了三个门来控制信息的传递，分别是遗忘门，输入门 和输出门 。三个门的作用为：
（1）遗忘门: 遗忘门𝑓𝑡控制上一时刻的内部状态 需要遗忘多少信息；
（2）输入门: 输入门𝑖𝑡控制当前时刻的候选状态 有多少信息需要保存；
（3）输出门: 输出门𝑜𝑡控制当前时刻的内部状态 有多少信息需要输出给外部状态 ；

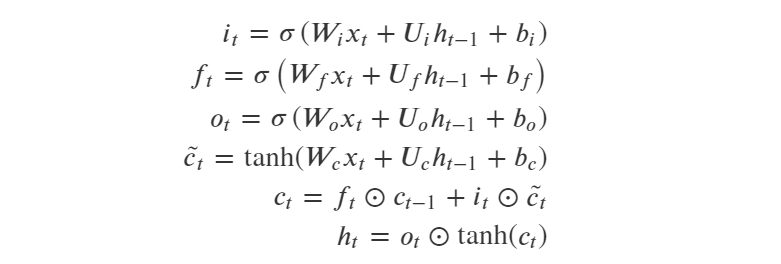
• GRU 结构解析：

GRU的结构比LSTM更为简单一些，GRU只有两个门，更新门和重置门 。
（1）更新门：更新门用于控制每一步ℎ𝑡被更新的比例，更新门越大，ℎ𝑡更新幅度越大。
（2）重置门：重置门用于控制更新候选向量ℎ̃ 𝑡中前一步的状态ℎ𝑡−1被重新放入的比例，重置门越大，更新候选向量中ℎ𝑡−1被重新放进来的比例越大。
公式中的小圈表示哈达玛积，也就是两个向量逐位相乘。
其中(1)式和(2)式计算的是更新门𝑢𝑡和重置门𝑟𝑡，是两个长度和ℎ𝑡相同的向量。
注意到(4)式 实际上和ResNet的残差结构是相似的，都是 f(x) = x + g(x) 的形式，可以有效地防止长序列学习反向传播过程中梯度消失问题。

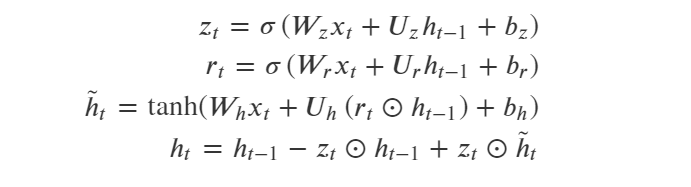
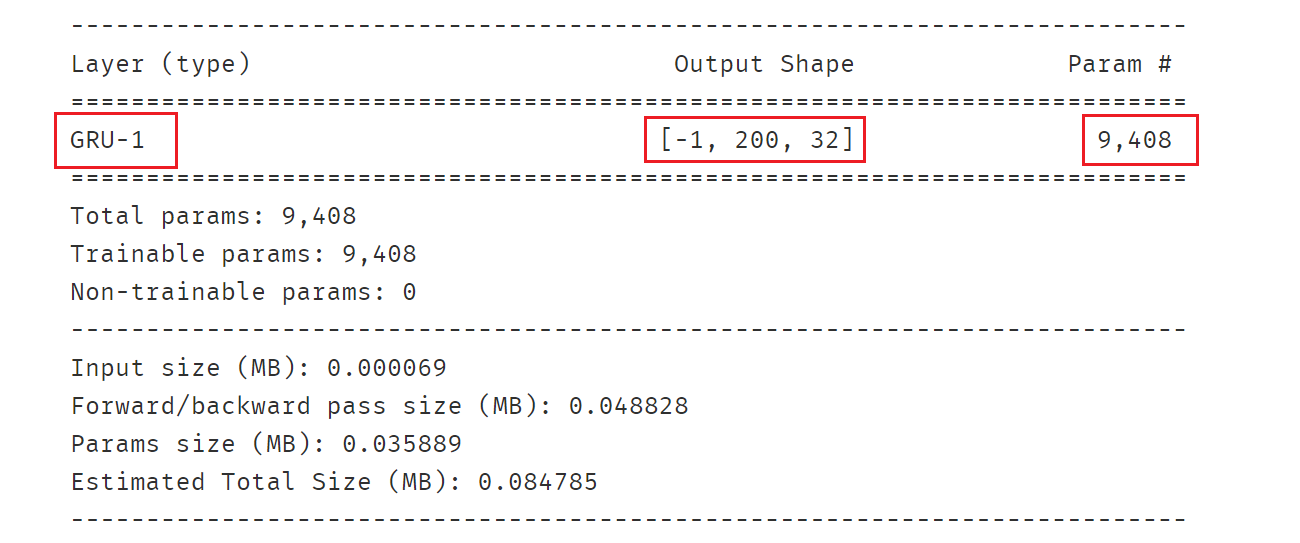
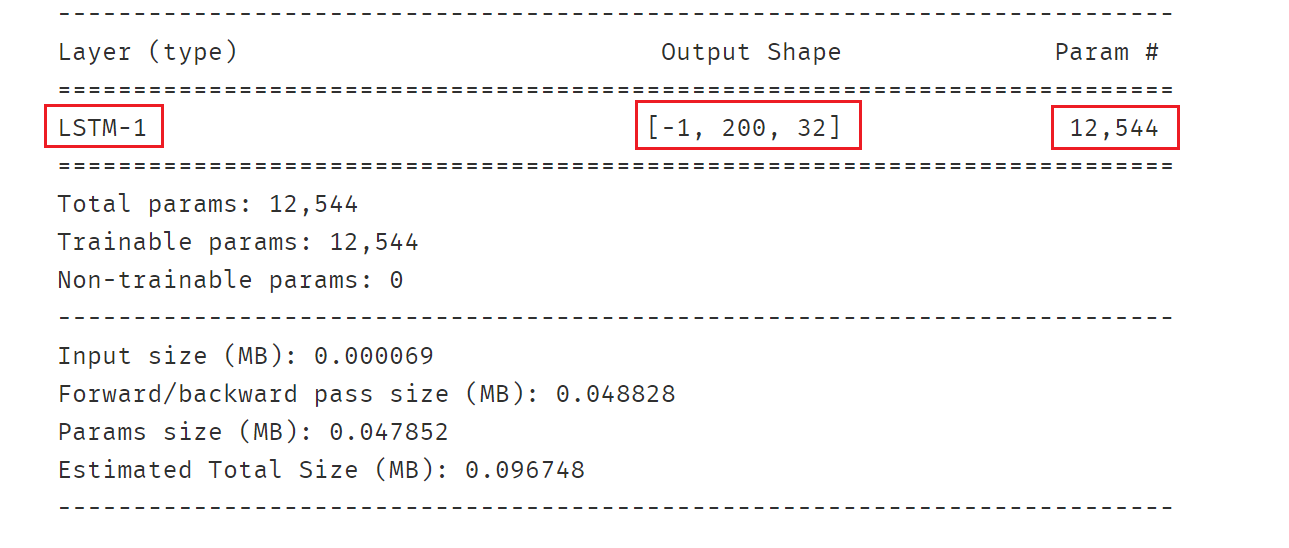
GRU的参数数量为LSTM的3/4。

import torch 
from torch import nn inputs = torch.randn(8,200,64) #batch_size, seq_length, featuresgru = nn.GRU(input_size=64,hidden_size=32,num_layers=1,batch_first=True)
gru_output,gru_hn = gru(inputs)
print("--GRU--")
print("gru_output.shape:",gru_output.shape)
print("gru_hn.shape:",gru_hn.shape)
print("\n")print("--LSTM--")
lstm = nn.LSTM(input_size=64,hidden_size=32,num_layers=1,batch_first=True)
lstm_output,(lstm_hn,lstm_cn) = lstm(inputs)
print("lstm_output.shape:",lstm_output.shape)
print("lstm_hn.shape:",lstm_hn.shape)
print("lstm_cn.shape:",lstm_cn.shape)

参考：https://github.com/lyhue1991/eat_pytorch_in_20_days