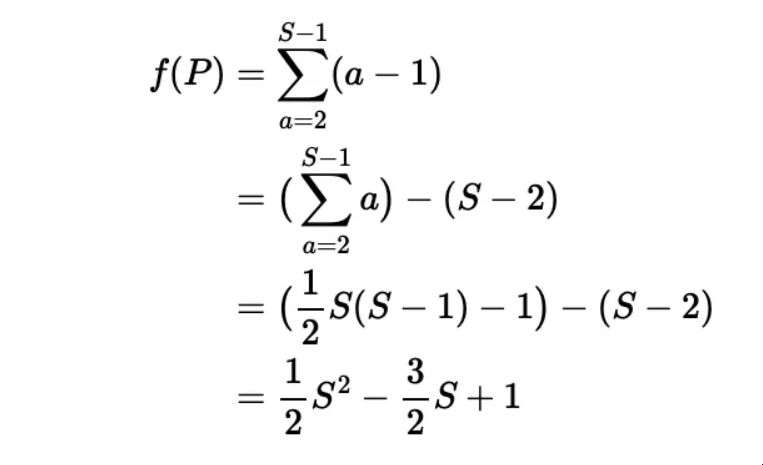进制
二进制 (Binary):0、1。简写为B
八进制(Octonary):0、1、2、3、4、5、6、7。简写为O
十进制(decimalism):0、1、2、3、4、5、6、7、8、9 简写为D
十六进制(hexadecimal):0、1、2、3、4、5、6、7、8、9、A(10)、B(11)、C(12)、D(13)、E(14)、F(15)。简写为H
二、八、十六进制转十进制
采用按权展开式的方法,其他进制类似,拿二进制举例:
1101(B) 转为十进制:
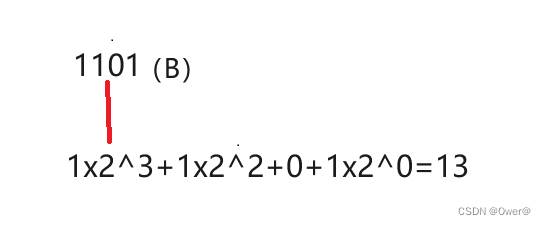
十进制转二、八、十六进制
采用短除法,拿八进制举例: 除八取余,直至商为0 ,余数结果倒叙排列。
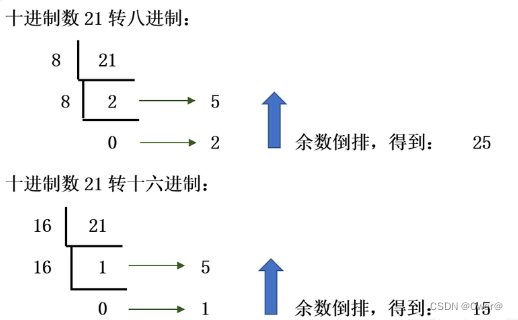
对于十进制转为八进制、十六进制,可以间接先求十进制转二进制求得。
二进制转八、十六进制
根据进制分组进行分别对每一组按权展开式,八进制为 2^3 (每三位一组),十六进制为 2^4(每四位一组),分组时整数从右到左划分,小数部分从左往右依次划分,不足补0。

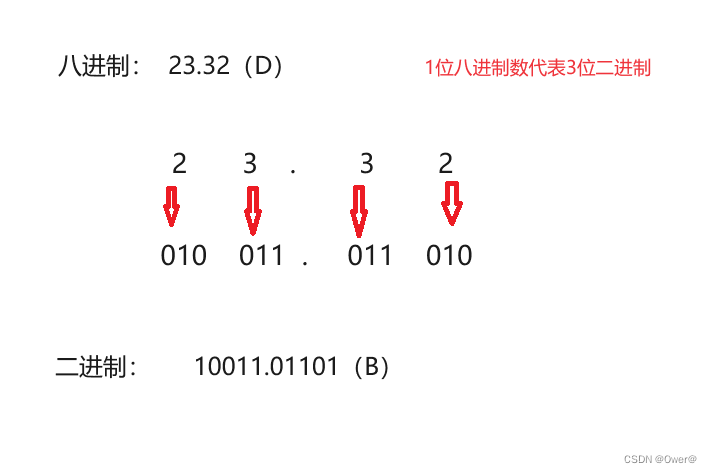
八、十六进制转二进制
分组,每一位进行短除法,除2取余,直至商为0,余数倒叙排列,小数部分类似。
小数十进制转二进制
小数部分乘2取整,直至余数为0,结果顺序排列。

小数二进制转十进制
按权展开式,整数部分从右往左,权值从0开始,小数部分从左往右,权值从-1开始
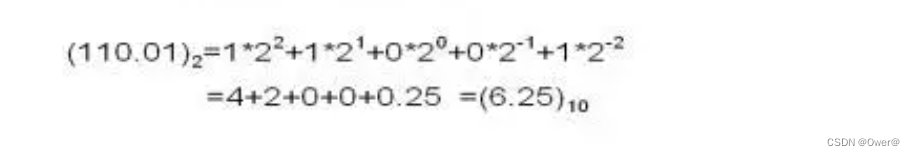
推荐进制转换工具
https://tool.oschina.net/hexconvert![]() https://tool.oschina.net/hexconvert
https://tool.oschina.net/hexconvert