目录
一、实验介绍
二、实验环境
1. 配置虚拟环境
2. 库版本介绍
三、实验内容
0. 导入库
1. 线性模型linear_model
2. 损失函数loss_function
3. 定义数据
4. 初始化权重和偏置
5. 模型训练
6. 迭代
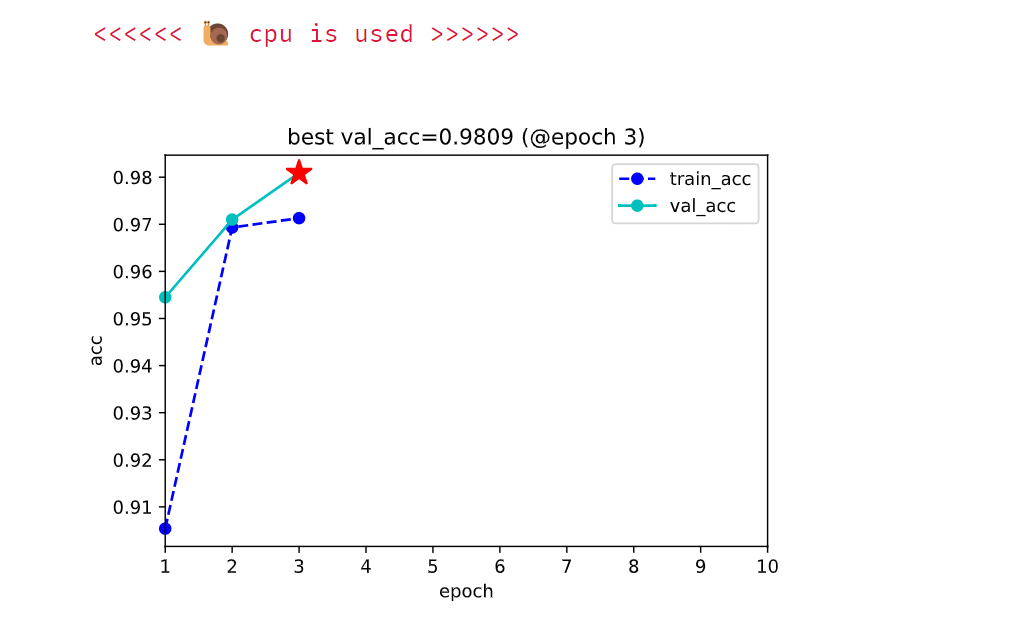
7. 实验结果
8. 完整代码
一、实验介绍
使用随机梯度下降优化器训练线性模型,并输出优化后的参数
二、实验环境
本系列实验使用了PyTorch深度学习框架,相关操作如下:
1. 配置虚拟环境
conda create -n DL python=3.7 conda activate DLpip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio==0.8.1 -f https://download.pytorch.org/whl/torch_stable.html
conda install matplotlib conda install scikit-learn2. 库版本介绍
| 软件包 | 本实验版本 | 目前最新版 |
| matplotlib | 3.5.3 | 3.8.0 |
| numpy | 1.21.6 | 1.26.0 |
| python | 3.7.16 | |
| scikit-learn | 0.22.1 | 1.3.0 |
| torch | 1.8.1+cu102 | 2.0.1 |
| torchaudio | 0.8.1 | 2.0.2 |
| torchvision | 0.9.1+cu102 | 0.15.2 |
三、实验内容
ChatGPT:
随机梯度下降(Stochastic Gradient Descent,SGD)是一种常用的优化算法,用于训练机器学习模型。它是梯度下降算法的一种变体,主要用于大规模数据集或高维参数空间的情况下。
梯度下降算法的目标是通过最小化损失函数来寻找模型参数的最优解。在传统的梯度下降算法中,每个训练周期(epoch)都需要计算整个训练集的梯度,然后更新模型参数。这种方法在大规模数据集上计算量较大,因为每个训练周期都需要遍历整个数据集。
与传统的梯度下降不同,随机梯度下降每次迭代仅使用一个样本(或一小批样本)来计算梯度,并更新模型参数。具体步骤如下:
- 初始化模型参数。
- 将训练数据集随机打乱顺序。
- 对于每个训练样本(或小批量样本):
- 计算模型对于当前样本的预测值。
- 计算损失函数对于当前样本的梯度。
- 根据梯度和学习率更新模型参数。
- 重复步骤3,直到达到预定的训练周期数或满足停止条件。
随机梯度下降的主要优点是计算效率高,尤其适用于大规模数据集。它也可以在每个训练周期中进行参数更新,因此可以更快地收敛。然而,由于每次迭代仅使用一个样本(或小批量样本),因此随机梯度下降的更新方向可能会更加不稳定,导致训练过程中的损失函数波动较大。为了缓解这个问题,可以使用学习率衰减、动量等技巧来改进算法。
本系列为实验内容,对理论知识不进行详细阐释
(咳咳,其实是没时间整理,待有缘之时,回来填坑)
0. 导入库
import torch1. 线性模型linear_model
该函数接受输入数据x,使用随机生成的权重w和偏置b,计算输出值output。这里的线性模型的形式为 output = x * w + b。
def linear_model(x):return torch.matmul(x, w) + b2. 损失函数loss_function
这里使用的是均方误差(MSE)作为损失函数,计算预测值与真实值之间的差的平方。
def loss_function(y_true, y_pred):loss = (y_pred - y_true) ** 2return loss3. 定义数据
-
生成一个随机的输入张量
x,形状为 (5, 1),表示有 5 个样本,每个样本的特征维度为 1。 -
生成一个目标张量
y,形状为 (5, 1),表示对应的真实标签。 - 打印数据的信息,包括每个样本的输入值
x和目标值y。
x = torch.rand(5, 1)
y = torch.tensor([1, -1, 1, -1, 1], dtype=torch.float32).view(-1, 1)
print("The data is as follows:")
for i in range(x.shape[0]):print("Item " + str(i), "x:", x[i][0], "y:", y[i])
4. 初始化权重和偏置
w = torch.rand(1, 1, requires_grad=True)
b = torch.randn(1, requires_grad=True)5. 模型训练
model = linear_model(x, w, b)
optimizer = optim.SGD([w, b], lr=0.01) # 使用SGD优化器6. 迭代
num_epochs = 100 # 迭代次数
for epoch in range(num_epochs):optimizer.zero_grad() # 梯度清零prediction = linear_model(x, w, b)loss = loss_function(y, prediction)loss.mean().backward() # 计算梯度optimizer.step() # 更新参数# print(w, b)if (epoch + 1) % 10 == 0:print(f"Epoch {epoch + 1}/{num_epochs}, Loss: {loss.mean().item()}")
-
在每个迭代中:
-
将优化器的梯度缓存清零,然后使用当前的权重和偏置对输入
x进行预测,得到预测结果prediction。 -
使用
loss_function计算预测结果与真实标签之间的损失,得到损失张量loss。 -
调用
loss.mean().backward()计算损失的平均值,并根据计算得到的梯度进行反向传播。 -
调用
optimizer.step()更新权重和偏置,使用优化器进行梯度下降更新。 -
每隔 10 个迭代输出当前迭代的序号、总迭代次数和损失的平均值。
-

7. 实验结果
print("The optimized parameters are:")
print("w:", model[0].item())
print("b:", model[1].item())
8. 完整代码
import torch
import torch.optim as optimdef linear_model(x, w, b):return torch.matmul(x, w) + bdef loss_function(y_true, y_pred):loss = (y_pred - y_true) ** 2return lossx = torch.rand(5, 1)
y = torch.tensor([1, -1, 1, -1, 1], dtype=torch.float32).view(-1, 1)
print("The data is as follows:")
for i in range(x.shape[0]):print("Item " + str(i), "x:", x[i][0], "y:", y[i])w = torch.rand(1, 1, requires_grad=True)
b = torch.randn(1, requires_grad=True)
model = linear_model(x, w, b)
optimizer = optim.SGD([w, b], lr=0.01) # 使用SGD优化器num_epochs = 100 # 迭代次数
for epoch in range(num_epochs):optimizer.zero_grad() # 梯度清零prediction = linear_model(x, w, b)loss = loss_function(y, prediction)loss.mean().backward() # 计算梯度optimizer.step() # 更新参数# print(w, b)if (epoch + 1) % 10 == 0:print(f"Epoch {epoch + 1}/{num_epochs}, Loss: {loss.mean().item()}")print("The optimized parameters are:")
print("w:", model[0].item())
print("b:", model[1].item())注意:
本实验使用随机瞎生成的数据,所以训练起来没有任何意义,下文将基于经典的鸢尾花数据集进行实验,并对模型进行评估。