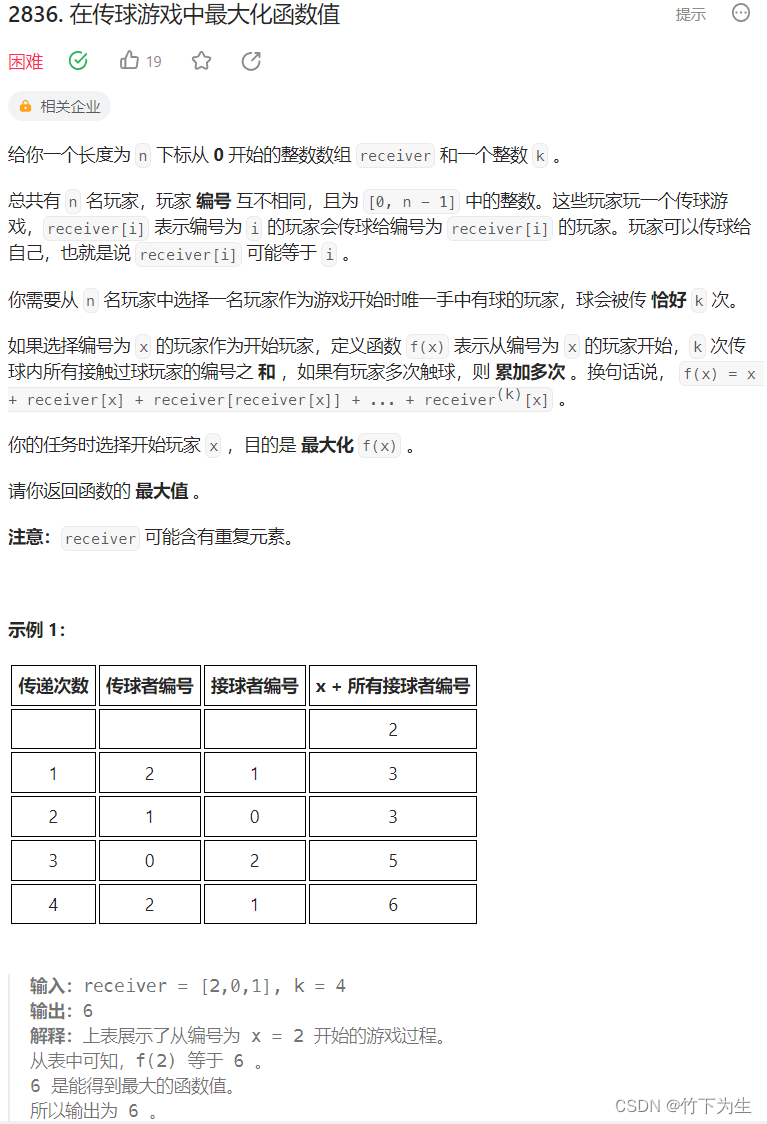
❓ 剑指 Offer 62. 圆圈中最后剩下的数字

难度：简单

0, 1, ··· ,n-1 这 n 个数字排成一个圆圈，从数字 0 开始，每次从这个圆圈里删除第 m 个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：

输入: n = 5, m = 3
输出: 3

示例 2：

输入: n = 10, m = 17
输出: 2

限制：

• $1<=n<=10^5$
• $1<=m<=10^6$

💡思路：约瑟夫环

全文重点：只关心最终活着那个人的序号变化！

举个栗子： n=8，m=3

我们定义 F(n, m)表示最后剩下那个人的索引号，因此我们只关系最后剩下来这个人的索引号的变化情况即可。

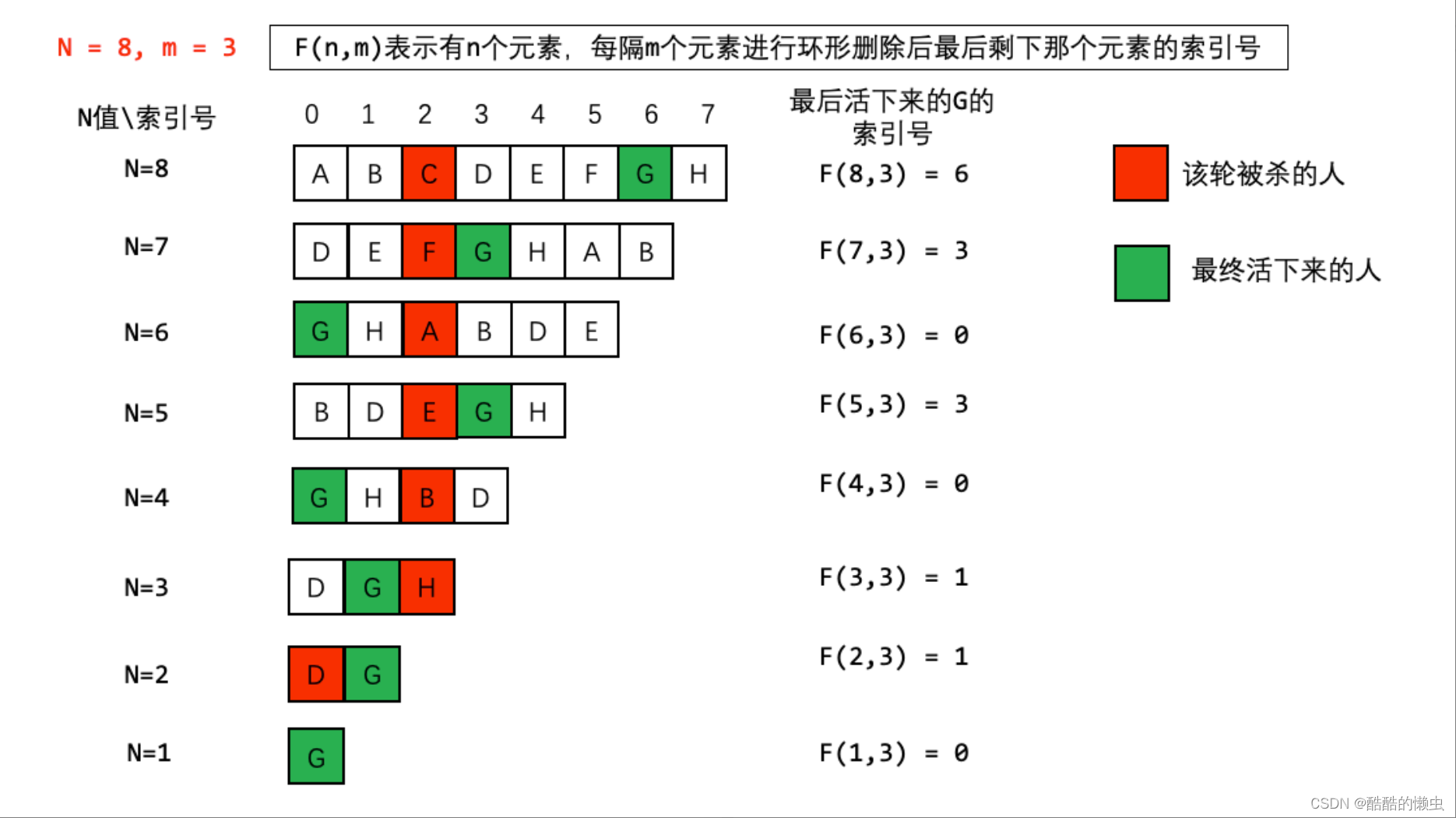
从8个人开始，每次杀掉一个人，去掉被杀的人，然后把杀掉那个人之后的第一个人作为开头重新编号

• 第一次 C 被杀掉，人数变成7，D作为开头，（最终活下来的 G 的编号从6变成3）
• 第二次 F 被杀掉，人数变成6，G作为开头，（最终活下来的 G 的编号从3变成0）
• 第三次 A 被杀掉，人数变成5，B作为开头，（最终活下来的 G 的编号从0变成3）
• 以此类推，当只剩一个人时，他的编号必定为0！（重点！）

最终活着的人序号的反推:

现在我们知道了 G 的索引号的变化过程，那么我们反推一下 从 n = 7 到 n = 8 的过程，如何才能将 n = 7 的排列变回到 n = 8 呢？

我们先把被杀掉的 C 补充回来，然后右移 m 个人，发现溢出了，再把溢出的补充在最前面

神奇了 经过这个操作就恢复了 n = 8 的排列了！

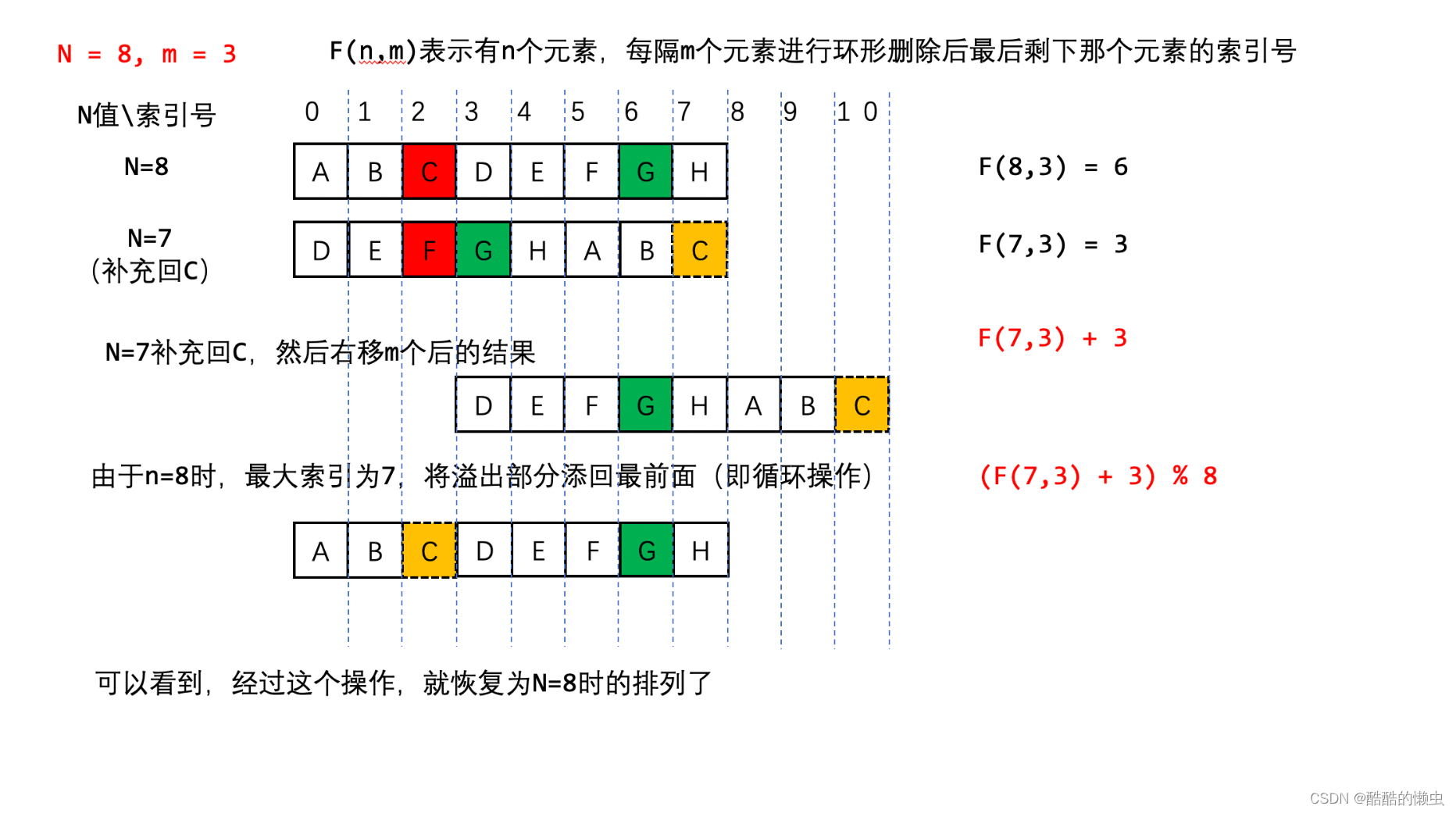
因此我们可以推出递推公式 f(8,3)=[f(7,3)+3]%8进行推广泛化，即
$$f(n,m)=[f(n-1,m)+m]\%n$$

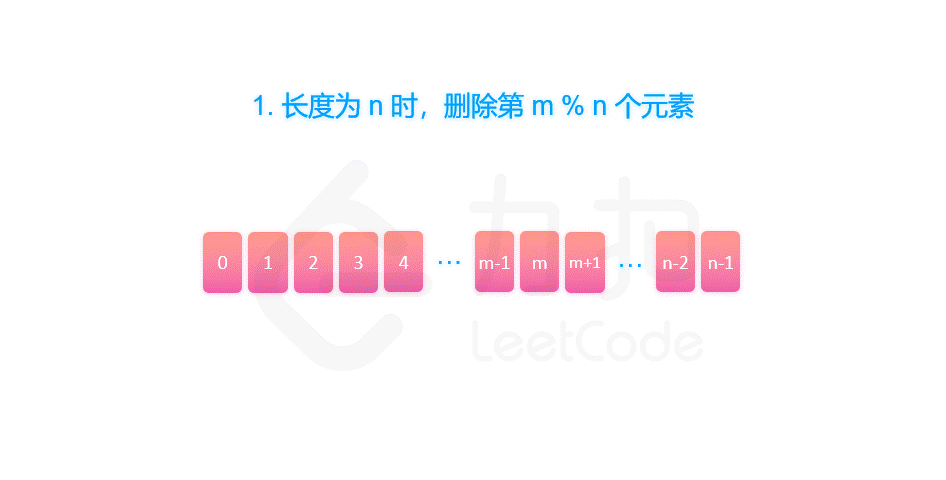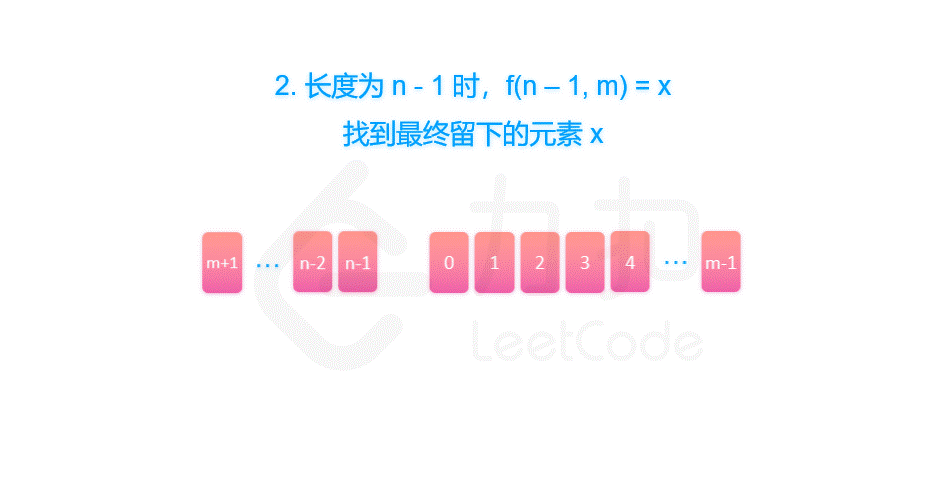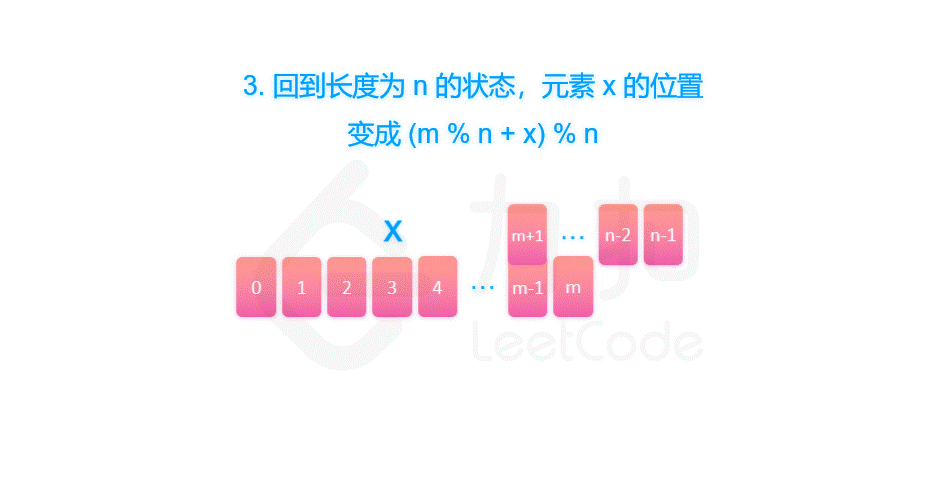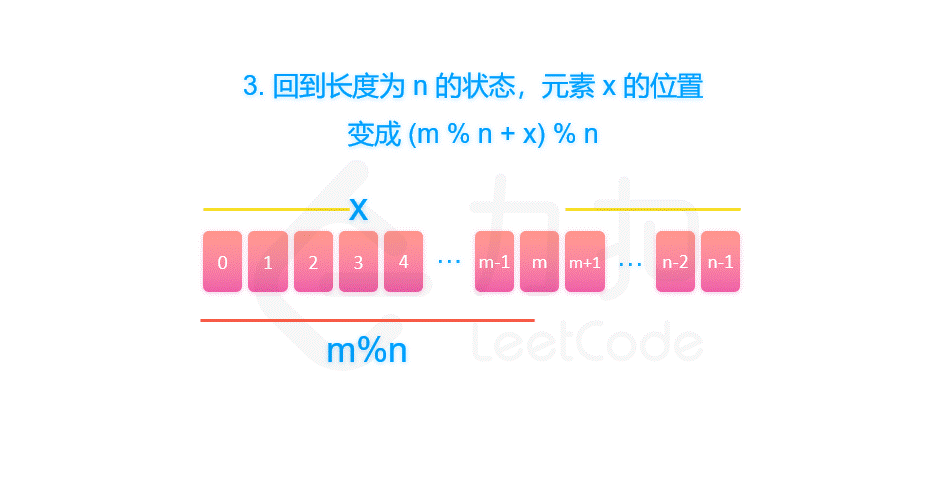
所以约瑟夫环，圆圈长度为 n 的解可以看成长度为 n-1 的解再加上报数的长度 m。因为是圆圈，所以最后需要对 n 取余。

🍁代码：(C++、Java)

递归：

C++

class Solution {
public:int lastRemaining(int n, int m) {if(n == 1) return 0;return (lastRemaining( n - 1, m) + m) % n;}
};

Java

class Solution {public int lastRemaining(int n, int m) {if(n == 1) return 0;return (lastRemaining( n - 1, m) + m) % n;}
}

迭代：
C++

class Solution {
public:int lastRemaining(int n, int m) {int f = 0;for (int i = 2; i != n + 1; ++i) {f = (m + f) % i;}return f;}
};

Java

class Solution {public int lastRemaining(int n, int m) {int f = 0;for (int i = 2; i != n + 1; ++i) {f = (m + f) % i;}return f;}
}

🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(n)$，需要求解的函数值有 n 个。
• 空间复杂度：$O(1)$，迭代需要常数级空间；而递归深度为 n，需要使用 $O(n)$ 的栈空间。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！