算法介绍

回溯法（Back Tracking Method）（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为 “回溯点”。

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就 “回溯” 返回，尝试别的路径。

可以把回溯法看成是递归调用的一种特殊形式。

回溯法思路的简单描述是：把问题的解空间转化成了图或者树的结构表示，然后使用深度优先搜索策略进行遍历，遍历的过程中记录和寻找所有可行解或者最优解。

回溯算法能解决的问题

• 组合问题：N个数里面按一定规则找出k个数的集合
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 棋盘问题：N皇后，解数独等等

解题模板

代码方面，回溯算法的框架：

result = []
def backtracking(路径, 选择列表):// 确定终止条件if 满足结束条件:result.add(路径)return// 单层搜索for 选择 in 选择列表:做选择backtracking(路径, 选择列表)撤销选择

核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。

总结就是：

循环 + 递归 = 回溯

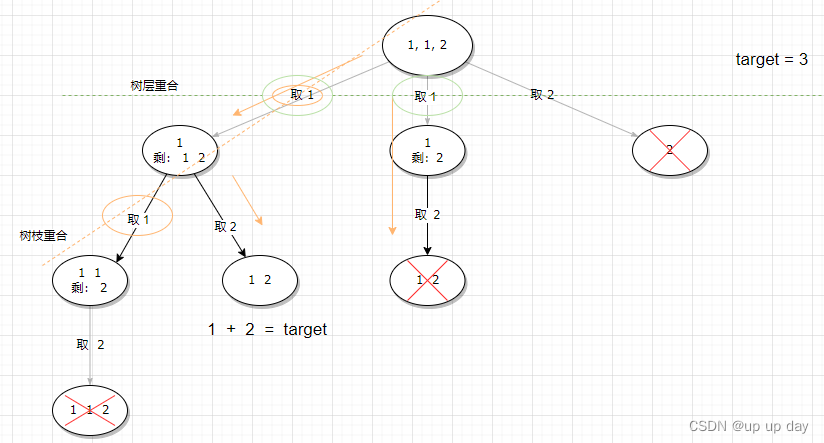
1. 组合问题

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过// used[i - 1] == false，说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把给candidates排序，让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};

这个组合问题中，最主要的问题是搞清楚 树层去重 和 树枝去重

2. N皇后问题

class Solution {
public:// 存放不同解法vector<vector<string>> result;void backtracking(int n, int row, vector<string> chessboard) {if(row == n) {result.push_back(chessboard);return;}for(int colu = 0; colu < n; colu++) {if(IsValid(n, row, colu, chessboard)) {  // 验证合法就可以放chessboard[row][colu] = 'Q';  // 放置皇后backtracking(n, row + 1, chessboard);chessboard[row][colu] = '.';  // 回溯，撤销皇后}}}bool IsValid(int n, int row, int colu, vector<string> chessboard) {// 检查放到此处是否有效， 同列、对角是否有其他皇后（回溯时每行只取一次，所以不用检查同行）// 向上检查同列是否有皇后for(int i = 0; i < row; i++) {if(chessboard[i][colu] == 'Q') {return false;}}// 检查 135°（左上）是否有皇后for(int i = row-1, j = colu - 1; i >= 0 && j >= 0; i--, j--) {if(chessboard[i][j] == 'Q') {return false;}}// 检查 45°（右上）是否有皇后for(int i = row-1, j = colu + 1; i >= 0 && j < n; i--, j++) {if(chessboard[i][j] == 'Q') {return false;}}return true;}vector<vector<string>> solveNQueens(int n) {// 棋盘初始化vector<string> chessboard(n, string(n, '.'));// n:棋盘大小 0：从棋盘0行开始选backtracking(n, 0, chessboard);return result;}
};