AB试验(三)一次试验的规范流程
一次完整且规范的A/B试验可参考下图:
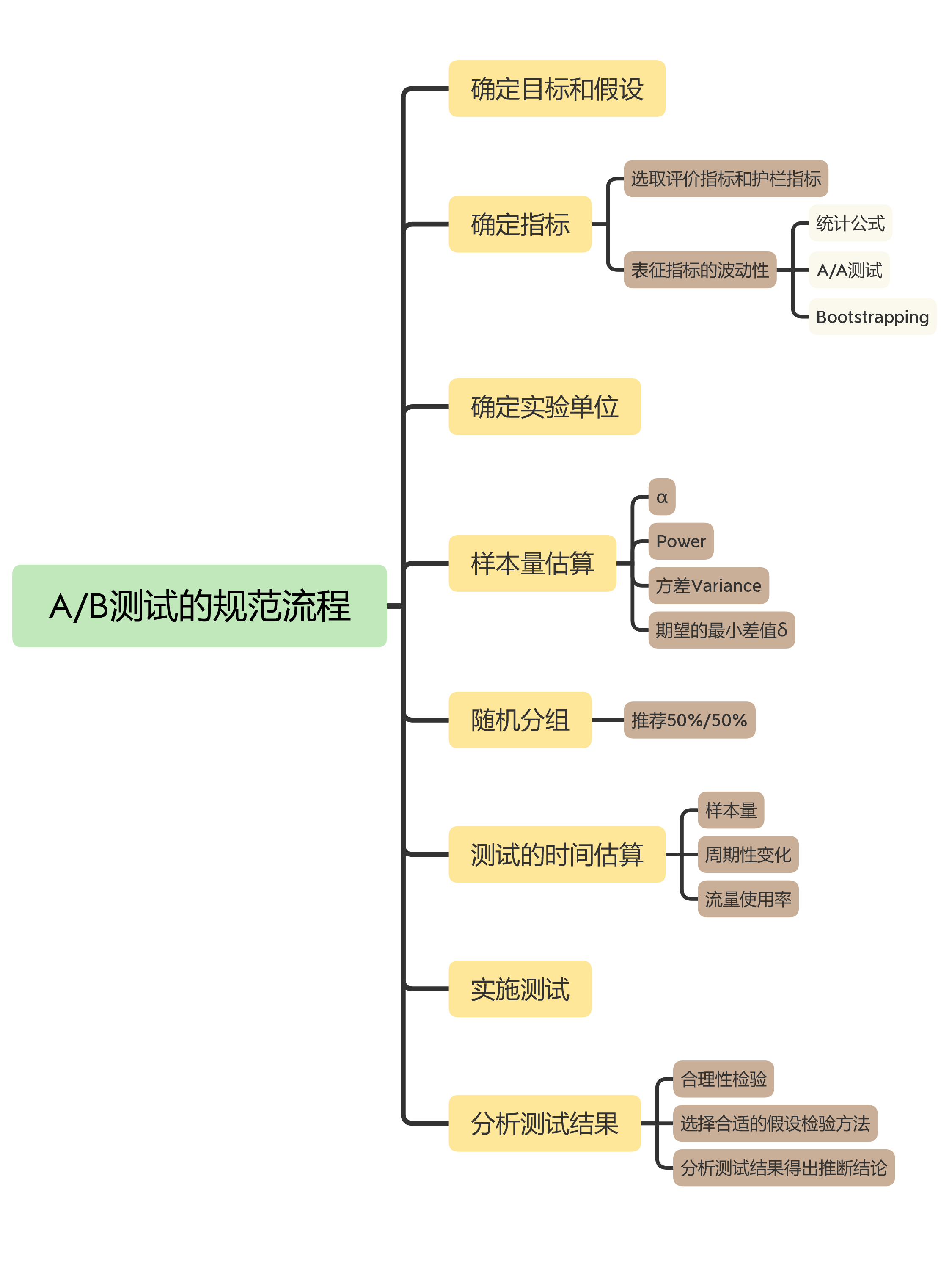
确定目标和假设
-
核心:A/B测试是因果推断,所以我们首先要确定原因和结果。目标决定了结果,而假设又决定了原因。
-
如何确定
- 分析问题,确定想要达到的结果(目标)
- 其次,提出解决业务问题的大致方案
- 最后,从大致解决方案中提取具体的假设(假设)
确定指标
指标类型
- 评价指标(Evaluation Metrics):能驱动公司实现核心价值的指标。通常是短期的、比较敏感、有很强的可操作性,例如点击率、转化率、人均使用时长等
- 护栏指标(Guardrail Metrics):衡量A/B测试是否符合业务上的长期目标,不会因为优化短期指标而打乱长期目标。例如退订率、用户体验等
评价指标的选取标准
-
可归因性:业务改动能引发指标变化
-
可测量性:指标的变化是易于统计量化的
-
敏感性与稳定性:如果实验中的变量变化了,评价指标要能敏感地做出相应的变化;但如果是其他因素变化了,评价指标要能保持相应的稳定性。
- 长期与短期指标:检测单次的变化时(比如单次推送/邮件)一般选用短期效果指标,因为长期效果目标通常对单次变化并不敏感。检测连续的、永久的变化时(比如增加产品功能),可以选用长期效果的指标
- A/A测试测量稳定性:如果A/A测试的结果发现两组的指标有显著不同,那么就说明要么分组分得不均匀,每组的数据分布差异较大;要么选取的指标波动范围太大,稳定性差。
- 回溯性分析来表征敏感性:回溯历史数据,其他的变动(非本次试验改动)是否会引起该指标的明显变化。
-
如何选取
- 历史经验:依据业务/产品所处阶段,例如起步阶段的拉新点击率、转化率等;发展与成熟阶段的平均使用时间、平均使用频率、留存率等。
- 目标抽象,可采用定性+定量的方法:例如用户满意度,可通过用户调研进行用户满意与不满意的分组,并计算一些指标,找出具有明显相关的指标进行替代借鉴
- 其他试验或网络公开试验的相关指标
- 构建总体评价标准OEC(Overall Evaluation Criteria)
亚马逊推送电子邮件的案例:
- 在实验组给用户发邮件,在对照组不给用户发邮件。起初的评级指标为收入,结果可想而知,实验组发的邮件越多,收入越高。但现实情况是用户收到一定程度的邮件后就会觉得是垃圾邮件,影响了用户体验而选择了退订,因此会带来预期之外的损失。
- 构建 O E C = ∑ i R e v e n u e − S ∗ U n s u b s c r i b e l i f e t i m e l o s s n OEC=\frac{\sum_i Revenue − S ∗ Unsubscribe_lifetime_loss}{n} OEC=n∑iRevenue−S∗Unsubscribelifetimeloss,i代表每一个用户,Revenue代表每组退订的人数,Unsubscribe_lifetime_loss代表用户退订邮件带来的预计损失,n代表每组的样本大小。
- 实施OEC后,发现有一半以上电子邮件的OEC都是负的,说明多发邮件并不是总能带来正收益
优点:综合各方面的指标才能把握总体的好处;避免多重检验问题
⚠️注意:当多个指标单位、大小不在一个尺度上时,需要进行归一化处理
-
衡量评价指标的波动性
-
根据统计公式计算:置信区间=样本均值 ± \pm ±z分数*标准误差
- 当样本量足够大时,数据服从正态分布,因此可采用z分数,一般我们选取95%的置信区间,对应的z分数为1.96
- 概率类指标标准误: S E = p ( 1 − p ) n SE=\sqrt{\frac{{p}(1-{p})}{n}} SE=np(1−p)
- 均值类指标标准误: S E = s 2 n = ∑ ( x i − x ˉ ) 2 n ( n − 1 ) SE=\sqrt\frac{s^2}{n}=\sqrt{\frac{\sum(x_i-\bar{x})^{2}}{n(n-1)}} SE=ns2=n(n−1)∑(xi−xˉ)2
-
经验法则:一些复杂指标不符合正态分布
- A/A测试:跑多个不同样本大小的A/A测试,然后分别计算每个样本的指标大小,计算出来后,再把这些指标从小到大排列起来,并且去除最小2.5%和最大2.5%的值,剩下的就是95%的置信区间
- Bootstrapping算法:先跑一个样本很大的A/A测试,然后在这个大样本中进行随机可置换抽样(Random Sample with Replacement),抽取不同大小的样本来分别计算指标。然后采用和A/A测试一样的流程:把这些指标从小到大排列起来,并且去除最小2.5%和最大2.5%的值,得到95%的置信区间。实际中更流行使用Bootstrapping算法,因此一些传统简单的指标也可以用该方法计算后与传统公式进行比较,如果差距较大则需要跑更多的A/A测试进行验证
-
护栏指标
- 业务品质层面:是在保证用户体验的同时,兼顾盈利能力和用户的参与度
- 网络延迟:网页加载时间、app响应时间等
- 闪退率
- 盈利能力:人均花费、人均利润等
- 用户参与度/满意度:人均使用时长、人均使用频率等
- 统计品质层面:统计方面主要是尽可能多地消除偏差,使实验组和对照组尽可能相似,比如检测两组样本量的比例,以及检测两组中特征的分布是否相似
- 实验/对照组中样本大小的比例
- 实验/对照组中样本特征的分布
确定实验单位
-
三个维度
-
用户层面:把单个的用户作为最小单位,也就是以用户为单位来划分实验组和对照组。常见的如:用户ID、匿名ID(cookies)、设备ID、IP地址。准确度上,用户ID>匿名ID>设备ID>IP地址
-
访问层面:每次访问作为最小单位,一个用户会有多个访问ID,所以该用户可能同时出现在实验组和对照组
-
页面层面:每一个"新"页面作为最小单位,例如每次回到首页记做一次页面浏览ID
-
三个维度之间的关系:一个用户可以有多个访问,一个访问可以有多个页面浏览,因此实验单位的颗粒度越来越细,获得的样本量也越来越多
-
经验总结:访问层面和页面层面的单位,比较适合变化不易被用户察觉的A/B测试,比如测试算法的改进、不同广告的效果等等;如果变化是容易被用户察觉的,那么建议你选择用户层面的单位
-
-
-
三大原则
- 保证用户体验的连贯性:即A/B测试中的变化是用户可以察觉的,实验单位就需要选择用户层面
- 实验单位要和评价指标的单位保持一致
- 再保证前两个原则的前提下,样本要尽可能的多
样本量估算
合适的样本量
- 样本量不是越多越好:时间成本+试错成本
- A/B测试所需的时间=总样本量/单位时间获取样本量。当所需样本量越小,实验时间越短,实际业务场景中,时间是最宝贵的资源。
- A/B实验中的改动也可能造成业务损害,因此需要一定的试错成本。当实验样本越小时,试错成本就会越低
- 样本量的平衡:在A/B测试中,既要保证样本量足够大,又要把实验控制在尽可能短的时间内
样本量计算原理
- 计算公式: n = ( Z 1 − α 2 + Z 1 − β ) 2 ( δ σ p o o l e d ) 2 = ( Z 1 − α 2 + Z p o w e r ) 2 ( δ σ p o o l e d ) 2 n=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{1-\beta})^2}{(\frac{\delta}{\sigma_{pooled}})^2}=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{power})^2}{(\frac{\delta}{\sigma_{pooled}})^2} n=(σpooledδ)2(Z1−2α+Z1−β)2=(σpooledδ)2(Z1−2α+Zpower)2
- Z 1 − α 2 Z_{1-{\frac{\alpha}{2}}} Z1−2α为 1 − α 2 1-\frac{\alpha}{2} 1−2α对应的z分数, Z p o w e r Z_{power} Zpower为(power)对应的z分数,
- δ \delta δ为实验组和对照组评价指标的差值
- σ p o o l e d 2 \sigma_{pooled}^2 σpooled2为实验组和对照组的综合方差
- 如何理解power
- p o w e r = 1 − β power=1-\beta power=1−β,即通过A/B测试探测到两者不同的概率
- 可理解为A/B测试的灵敏度,power越大,越能探测到两组的不同
- 样本量n的四个影响因素
- 显著性水平 α \alpha α:显著水平 α \alpha α越小样本量越大(第一类错误越小,结果越精确,所需的样本量自然就越大)
- 功效 p o w e r ( 1 − β ) power(1-\beta) power(1−β):功效power越大样本量越大(第二类错误越小,结果越精确,所需的样本量自然就越大)
- 实验组和对照组的综合方差 σ p o o l e d 2 \sigma_{pooled}^2 σpooled2:综合方差越大样本量越大(综合方差越大,说明评价指标的波动范围越大,也越不稳定,那就更需要更多的样本来进行实验,从而得到准确的结果。)
- 实验组和对照组评价指标的差值 δ \delta δ:差值 δ \delta δ越小样本量越大(因为实验组和对照组评价指标的差值越小,越不容易被A/B测试检测到,所以我们需要提高Power,也就是说需要更多的样本量来保证准确度)
实践中如何计算样本量
-
参数默认设置:
-
日常设置 α = 5 % \alpha=5\% α=5%, p o w e r = 80 % power=80\% power=80%,所以 n ≈ 8 σ p o o l e d 2 δ 2 n \approx \frac{8\sigma_{pooled}^2}{\delta^2} n≈δ28σpooled2
-
样本均分:只有两组均分,才能使两组的样本量均达到最大,并且使总样本量发挥最大使用效率,从而保证A/B测试更快更准确地进行。所以此时 n ≈ 2 ∗ 8 σ p o o l e d 2 δ 2 n \approx 2 * \frac{8\sigma_{pooled}^2}{\delta^2} n≈2∗δ28σpooled2
非均分样本的缺点:
- 在非均分的情况下,只有相对较小组的样本量达到最小样本量,实验结果才有可能显著,并不是说实验组越大越好,因为瓶颈是在样本量较小的对照组上
- 准确度降低。如果保持相同的测试时间不变,那么对照组样本量就会变小,测试的Power也会变小,测试结果的准确度就会降低
- 延长测试时间。如果保持对照组的样本量不变,那么就需要通过延长测试时间来收集更多的样本
-
-
估算实验组和对照组评价指标的差值 δ \delta δ
- 从收益和成本的角度进行估算:业务变动会带来一定的额外成本(包括不限于人力成本、时间成本、维护成本、机会成本等,也会带来一定的额外收益,因此可以计算指标至少提高多少才能使得净收益为正。
- 通过历史数据计算评价指标的波动范围:置信区间=样本均值 ± \pm ±z分数*标准误差(同衡量评价指标的波动性),因此可以计算指标至少提高多少才能高出波动范围的最大值。
-
计算实验组和对照组的综合方差 σ p o o l e d 2 \sigma_{pooled}^2 σpooled2
-
概率类指标: σ p o o l e d 2 = p t e s t ( 1 − p t e s t ) + p c o n t r o l ( 1 − p c o n t r o l ) \sigma_{pooled}^2=p_{test}(1-p_{test})+p_{control}(1-p_{control}) σpooled2=ptest(1−ptest)+pcontrol(1−pcontrol)
- p c o n t r o l p_{control} pcontrol为对照组中事件发生的概率,即在没有A/B实验下,通过历史数据计算得到。
- p t e s t = p c o n t r o l + δ p_{test}=p_{control}+\delta ptest=pcontrol+δ, δ \delta δ为上个步骤预估的差值
-
均值类指标: σ p o o l e d 2 = 2 ∗ ∑ i n ( x i − x ˉ ) 2 n − 1 \sigma_{pooled}^2=\frac{2*\sum_{i}^{n}(x_i - \bar x)^2}{n-1} σpooled2=n−12∗∑in(xi−xˉ)2
- n为所取历史数据样本的大小
- x i x_i xi为所取历史数据样本中第i个用户的使用时长/购买金额等均值类指标
- x ˉ \bar x xˉ为所取历史数据样本中用户的平均使用时长/购买金额等
-
示例:优化app某一功能,提高用户注册率。计算所需的样本量
- 通过收益成本角度,估算 δ 收支平衡 = 8.2 % \delta_{收支平衡}=8.2\% δ收支平衡=8.2%
- 通过概率类指标计算 σ p o o l e d 2 = p t e s t ( 1 − p t e s t ) + p c o n t r o l ( 1 − p c o n t r o l ) \sigma_{pooled}^2=p_{test}(1-p_{test})+p_{control}(1-p_{control}) σpooled2=ptest(1−ptest)+pcontrol(1−pcontrol)。其中已知当前注册率约为60%,则 p t e s t = 60 % + 8.2 % = 68.2 % p_{test}=60\%+8.2\%=68.2\% ptest=60%+8.2%=68.2%。代入得 σ p o o l e d 2 = 0.46 \sigma_{pooled}^2=0.46 σpooled2=0.46
- n ≈ 8 ∗ 0.46 0.08 2 2 ≈ 548 n \approx \frac{8*0.46}{0.082^2} \approx 548 n≈0.08228∗0.46≈548,实验组与对照组样本量一致,则总样本为1096
-
随机分组
-
实验分组的要求:在同一时间维度下,让组成成分相似的用户群参与到两组实验
- 定义:具体表现就是每个指标在AB两组中要均衡,一个好的办法是通过马氏距离来定义相似性: d ( G 1 , G 2 ) = ( x ˉ 1 − x ˉ 2 ) T Σ ^ − 1 ( x ˉ 1 − x ˉ 2 ) d(G_1, G_2)=(\bar{x}_1-\bar{x}_2)^T \hat{\Sigma}^{-1}(\bar{x}_1-\bar{x}_2) d(G1,G2)=(xˉ1−xˉ2)TΣ^−1(xˉ1−xˉ2)
- 原因:只有排除其他协变量对实验的影响,实验差异才能归因于测试变量的差异
- 如何实现样本相似
- 随机化:界普遍使用完全随机分组法(Complete Randomization,CR),即对用户ID字段进行哈希后对100取模,得到一个结果值,再将结果值相同的用户分入同一个桶
- AA测试规避:不加策略对两组用户进行实验空跑,观察基准指标是否显著差异。若存在差异,则重新分组再重跑实验,直至基准指标基本一致
- RR(Rerandomization):即在每次CR分组之后, 验证CR的分组结果组间差异是否小于实验设定阈值(例如0.1),相对于CR而言, RR是通过牺牲计算时间, 进行分组尝试.。相当于AA测试的工程自动化
- 自适应分组算法(Adaptive):相比于传统的CR分组,Adaptive分组的算法更加复杂,在遍历人群进行分组的同时,每个组都需要记录目前为止已经分配的样本数,以及已经分配的样本在选定的观测指标上的分布情况。
- 实验结果差异的要求:假设A组的结果为 r 1 r_1 r1,B组的结果为 r 2 r_2 r2,则AB测试的差异为 δ = r 1 − r 2 \delta=r_1-r_2 δ=r1−r2。 δ \delta δ为依赖测试样本的随机变量。应该满足以下特性:
- 无偏性:假设在1%流量上某功能可以提高10%的点击率,那么在全量上也应该大约提高10%
- 低方差:方差越小,可靠性越高
-
实验分组方式:利用分层和分流的机制保证本站的流量高可用
-
原因:流量是有限且宝贵的;实验对象是多层的或者同一层内互不干扰的;AB测试的需求是大量的
-
正交实验:每个独立实验为一层,层与层之间流量是正交的,一份流量穿越每层实验时,都会再次随机打散,且随机效果离散。流量正交让业务关联度很小的实验有足够的流量同时进行(实现流量的高可用)
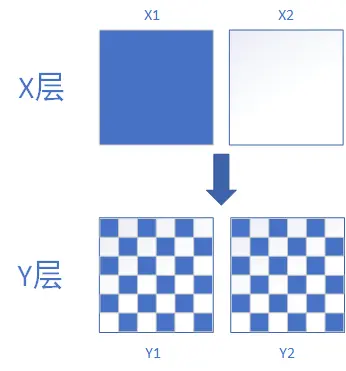
-
互斥实验:实验在同一层拆分流量,且不论如何拆分,不同组的流量是不重叠的。流量互斥让业务关联度较大的实验流量分开,避免干扰,保证实验结果的可信度。
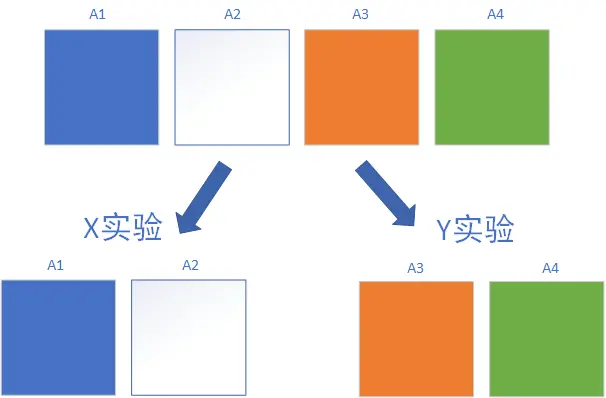
-
分层分流规则
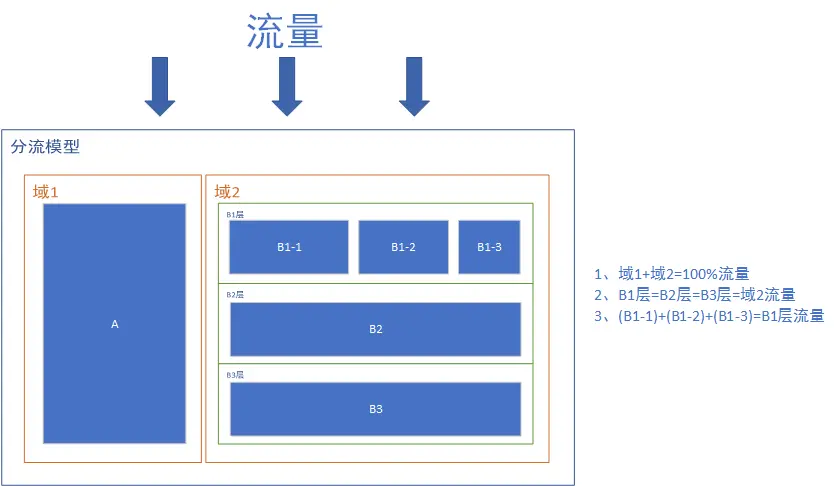
规则详述:
- 流量从上往下流过分流模型
- 域1和域2拆分流量,此时域1和域2是互斥的
- 流量流过域2中的B1层、B2层、B3层时,B1层、B2层、B3层的流量都是与域2的流量相等。此时B1层、B2层、B3层的流量是正交的
- 流量流过域2中的B1层时,又把B1层分为了B1-1,B1-2,B1-3,此时B1-1,B1-2,B1-3之间又是互斥的
应用场景
- 如果要同时进行UI优化、广告算法优化、搜索结果优化等几个关联较低的测试实验,可以在B1、B2、B3层上进行,确保有足够的流量
- 如果要针对某个按钮优化文字、颜色、形状等几个关联很高的测试实验,可以在B1-1、B1-2、B1-3层上进行,确保实验互不干扰
- 如果有个重要的实验,但不清楚当前其他实验是否对其有干扰,可以直接在域1上进行,确保实验结果准确可靠
-
-
用户进入实验的简单流程
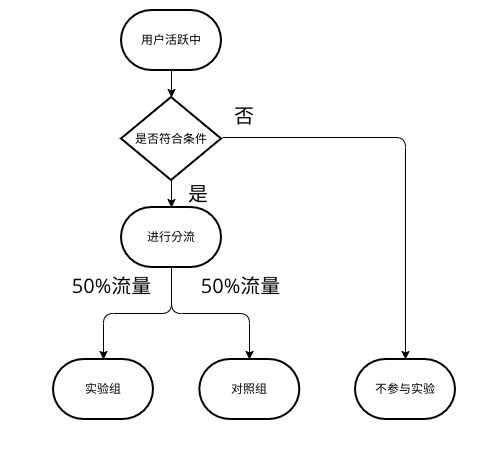
测试时间的估算
- AB实验所需时间=总样本量/单位时间能得到的样本量
- 用户行为的周期性:大部分场景下,用户在周末与工作日的表现有明显差异,因此一次实现最少需要包含一周的时间
实施测试
- 初始应同比例分配极小的流量,例如1%,观察试验是否正常运行,如果存在问题(包括不限于投诉陡升、退订退费陡升、未监测到功能改变、没上报埋点等),应该及时停止试验并回滚
- 若上述未发现异常情况,则可开始正常增加流量。如果实验中发现实验组数据明显较差,应该及时停止试验并回滚
- 一般性的,试验开始阶段置信区间都是非统计显著的,随着时间开始逐渐收敛。等到收集到所需样本且达到运行所需时间时。可以开始统计数据进行后续分析
分析测试结果
不要提前结束测试
- 由于样本量是不断变化的,所以每次观测都可以算作一次实验。统计上,A/B测试一般有5%的第一类错误率 α \alpha α,也就是说每重复100次测试平均能得到5次错误的统计显著性结果。即存在多重检验问题
- 提前观测到统计显著的结果,这就意味着样本量并没有达到事先估算的最小样本量,那么这个所谓的“统计显著的结果”就极有可能是错误的假阳性(False Positive)。即两组事实上是相同的,而测试结果错误地认为两组显著不同
保障统计品质的合理性检验
-
检验实验/对照组的样本比例是否一致
- 测试数据要么属于实验组,要么属于对照组,符合二项分布。如果流量等分,则进入实验组的概率为0.5
- 根据二项分布的公式计算标准误差 S E = p ( 1 − p ) n SE=\sqrt{\frac{{p}(1-{p})}{n}} SE=np(1−p)。然后以进入实验组的概率为中心构造置信区间
- 最后确认实际的实验组占总体样本比例是否在置信区间内,同理可计算对照组的。
- 举个例子:在一次等流量测试中,实验组样本是315256,对照组样本是315174。由于等流量分组,因此样本进入实验组的概率 p = 0.5 p=0.5 p=0.5,则 S E = 0.5 ( 1 − 0.5 ) 315256 + 315174 = 0.06 % SE=\sqrt{\frac{{0.5}(1-{0.5})}{315256+315174}}=0.06\% SE=315256+3151740.5(1−0.5)=0.06%。则进入实验组的置信区间为 [ 0.5 − 1.96 ∗ 0.06 % , 0.5 + 1.96 ∗ 0.06 % ] = [ 49.88 % , 50.12 % ] [0.5-1.96*0.06\%, 0.5+1.96*0.06\%]=[49.88\%,50.12\%] [0.5−1.96∗0.06%,0.5+1.96∗0.06%]=[49.88%,50.12%]。进入对照组也如此。计算实际的实验组占比和对照组占比分别为50.01%、49.99%,都在置信区间内,因此该次实验的两组样本量的比例通过了合理性检验
-
检验实验/对照组中特征的分布
- 常用的特征包括:年龄、性别、地点、设备、活跃情况等信息
- 特征分布合理性检验:卡方检验、KS检验、相对熵(KL散度、JS散度)、PSI
-
检验不通过该怎么办
- 产生的问题:实验/对照组样本量的比例和实验设计不相同时会出现样本比例不匹配问题(Sample Ratio Mismatch),实验/对照组的特征分布不相似则会导致辛普森悖论问题(Simpson Paradox)
- 如何解决
- 和工程师一起从实施的流程方面进行检查,看看是不是具体实施层面上两组有偏差或者bug。
- 从不同的维度来分析现有的数据,看看是不是某一个特定维度存在偏差。常用的维度有时间(天)、操作系统、设备类型等。比如从操作系统维度,去看两组中iOS和Android的用户的比例是否存在偏差,如果是的话那说明原因和操作系统有关
如何分析A/B测试结果
- p值法:当P值小于5%时,说明两组指标具有显著的不同。当P值大于5%时,说明两组指标没有显著的不同
- 置信区间法:如果置信区间包括0的话,两组指标没有显著不同。而如果置信区间不包括0的话,两组指标是显著不同的
经验总结:一般地两种方法是等价的,取其一即可。如果需要考虑成本收益的话,建议选择置信区间法,且要求差值 δ \delta δ的置信区间范围要比收支平衡时计算的 δ 收支平衡 \delta_{收支平衡} δ收支平衡要大
总结
从确定目标和假设,到确定评价指标和护栏指标,到确定实验单位,到样本量估算,到随机分组,到测试时间的估算,到实施测试,到分析测试结果,每一步都有规范的操作,所以在日常中按照此步骤规范操作,不仅能防止误操作,还能定位误操作的原因。
共勉~