完整程序：

clear
clc
%% 初始化参数
delta_t = 0.1;  %采样时间
T = 8;          %总运行时长
t = 0:delta_t:T;  %时间序列
N = length(t);  %序列的长度  
x0 = 0;  %初始位置
u0 = 0;  %初速度
U = 10;  %控制量、加速度

F = [1 delta_t
    0 1];   %状态转移矩阵
B = [0.5*delta_t^2  
    delta_t];  %控制矩阵
H = [1 0];  %观测矩阵
W = [0;3];  %过程噪声
V = [70];  %量测噪声

%分配空间 
XP = zeros(2,N);%预测值
XP(:,1) = [x0;u0];
XR = zeros(2,N);%真实值
XR(:,1) = [x0;u0];
Z = zeros(1,N);%观测值
Z(1) = [0];

for i=2:N
    XP(:,i) = F*XP(:,i-1)+B*U;  %预测值
    XR(:,i) = F*XR(:,i-1)+B*U+sqrt(W)*randn;  %真实值
    Z(i) = H*XR(:,i)+sqrt(V)*randn;  %观测值
end

%% 卡尔曼滤波%%
%初始化参数
Xk = zeros(2,N);  %最优估计值
Xk(:,1) = [0;0];
P = [1,0;0,1];  %均方误差
I = eye(2);
Q = [0 0;0 0.1];
R = 10;
for i=2:N
    
    %时间更新
    X_pre = F*Xk(:,i-1)+B*U;  %状态预测值
    P_pre = F*P*F'+Q;     %预测均方误差
    
    %量测更新
    Kg = P_pre*H'*inv(H*P_pre*H'+R);  %计算卡尔曼增益
    Xk(:,i) = X_pre+Kg*(Z(:,i)-H*X_pre);  %状态估计值
    P = (I-Kg*H)*P_pre;  %均方误差
end

%% 结果
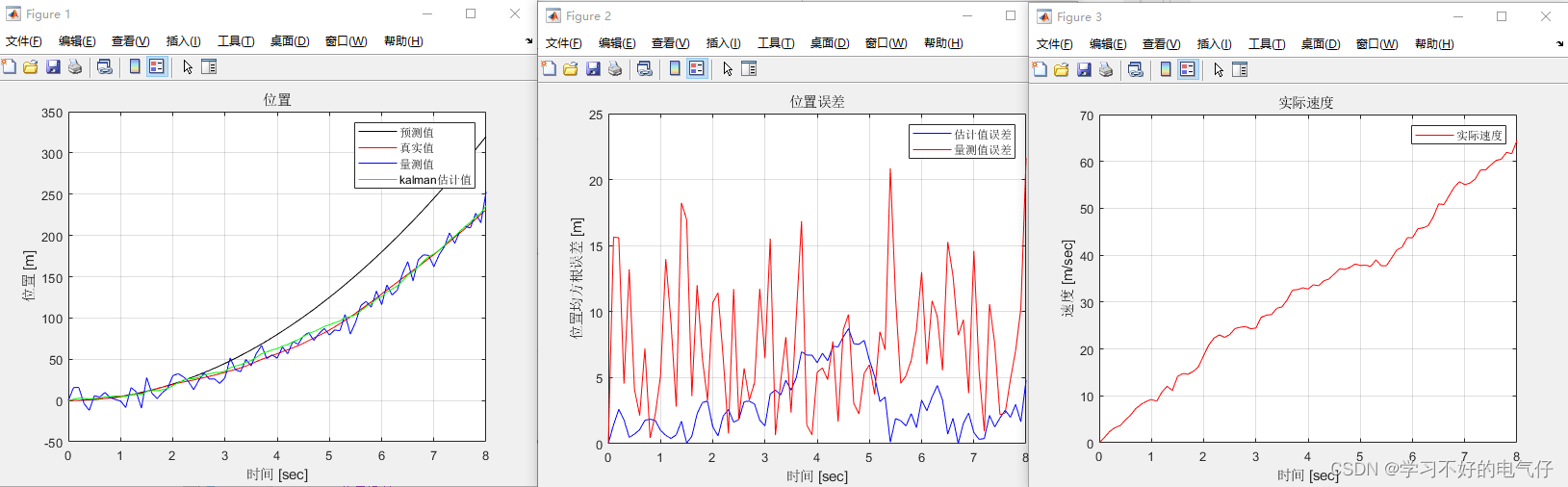
figure(1)
plot(t,XP(1,:),'K');hold on
grid on
plot(t,XR(1,:),'r');hold on
plot(t,Z(:),'b');
legend('预测值', '真实值','量测值');
title('位置')
xlabel('时间 [sec]')
ylabel('位置 [m]')
hold on
plot(t,Xk(1,:),'g');
legend('预测值', '真实值','量测值','kalman估计值');

figure(2)
x_error = abs(XR-Xk(1,:));
x_error1 = abs(XR-Z(1,:));
plot(t,x_error(1,:),'b'),grid on;hold on 
plot(t,x_error1(1,:),'r');
legend('估计值误差', '量测值误差');
title('位置误差')
xlabel('时间 [sec]')
ylabel('位置均方根误差 [m]')
grid on
hold off;

figure(3)
plot(t,Xk(2,:),'r'),grid on;
title('实际速度 ')
legend('实际速度')
xlabel('时间 [sec]')
ylabel('速度 [m/sec]')
hold off;