pytorch学习1

前言

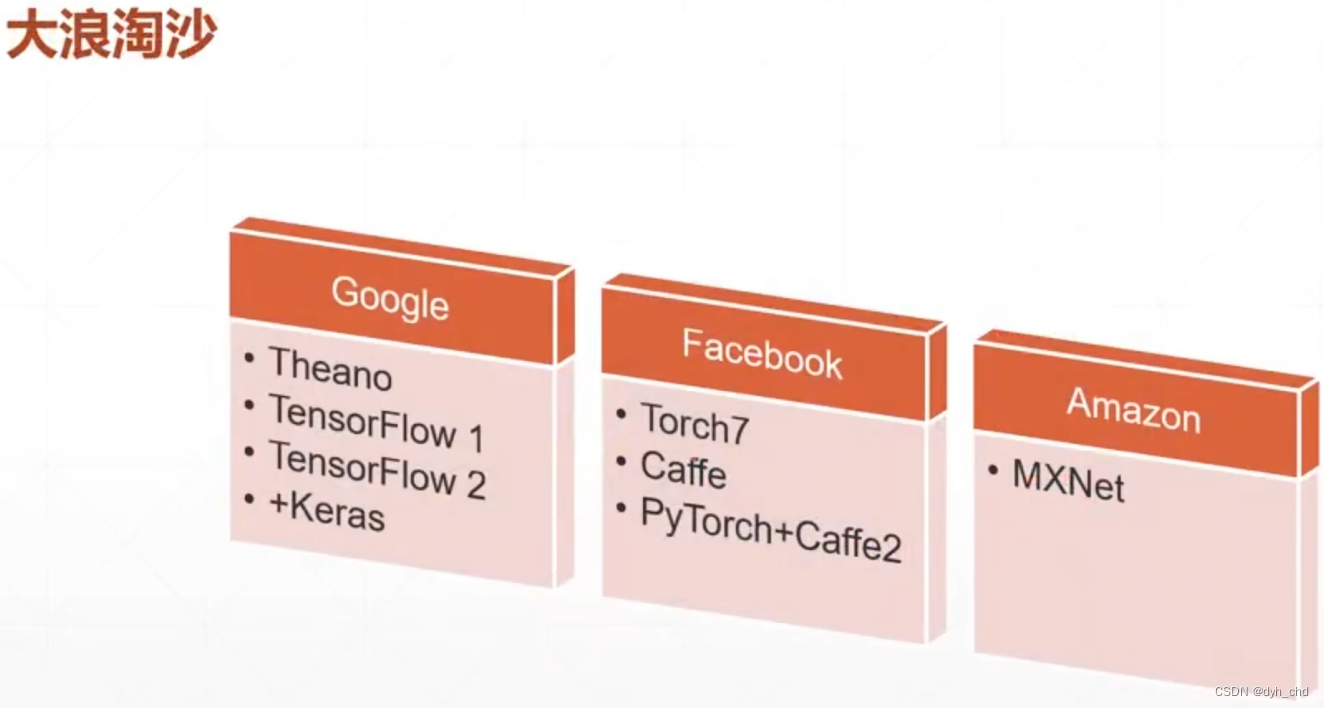
在这里插入图片描述
王者之争

核心之争在于动态图优先还是静态图优先
pytorch是动态计算生成新变量
tf是先定义变量，再生成

回归问题

1、梯度下降算法了解

[梯度算法是深度学习的核心，deep learning求解复杂问题主要靠的是梯度下降算法，故deep learning 近似等于 gradient programing.]

在这里插入图片描述
类似于高中所学的求导问题，求解loss的极小值，loss也可以看作我们熟悉的y，求y的倒数，再检验这个导数是否是我们要求解的极大值/极小值；梯度下降算法不同的是，它有迭代计算的过程。

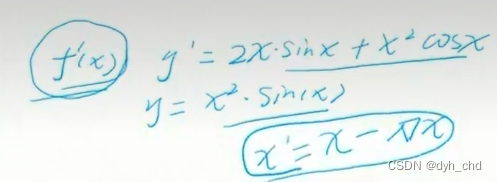
在这里插入图片描述
迭代得到新的x`等于x减去导数，以x轴坐标2.5为例：

在x=2.5点处，假设算得导数为-0.9，此时设定学习率即lr为0.005，则：
x`= 2.5 - （-0.9 * lr）

对于lr大小的设置，若lr设置的比较小，就会进行多次迭代，如上图中多的红点即为迭代记录
在这里插入图片描述
最终在x=5位置处导数为0，新的x`= 5 - 0.005 * 0，故得到的结果还是5。
当然，在实际计算中不一定正好达到5的位置，最终结果会接近于5。

在梯度下降计算中还有多种计算器的选择（如下），旨在增加一定的约束条件从而达到更好的计算结果，本质计算过程还是不变。
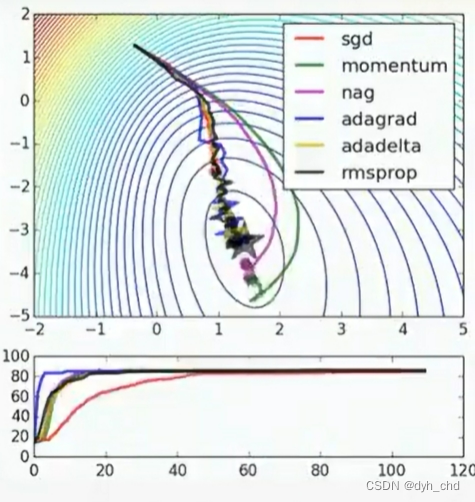
在这里插入图片描述
其中，最常用的是sgd、rmsprop还有图上没提到的adam。

2、简单回归问题

二元一次方程如下：
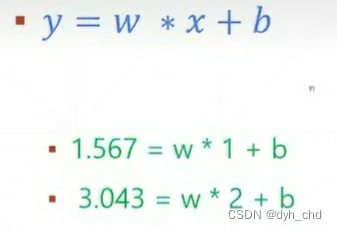
在这里插入图片描述
对于初中数学消元法来说，有（1，1.567）和（2，3.043）两组数据代入方程，由式2减去式1，w等于1.477，b约等于0.089。

上述能够精确求解的情况叫作Closed Form Solition。但实际上能够被精确求解的问题并不多，很多数据存在一定的偏差，实际问题往往都是求得一个近似解，在经验上被证明可行即为近似最优解。

在这里插入图片描述
实际数据会存在客观或人为的噪声误差，我们不可能只取两三组数据就求得一个准确的解，这时需要通过若干组数据去求得一个更平均的近似解。

这里并不是要得到y的最小值，而是要求得w和b，使w * x + b最接近于y，则此时梯度下降计算式可列为：
loss = （w * x + b - y）** 2
loss >= 0 ，求解loss的最小值即求得y近似等于w * x + b时，w和b的取值。

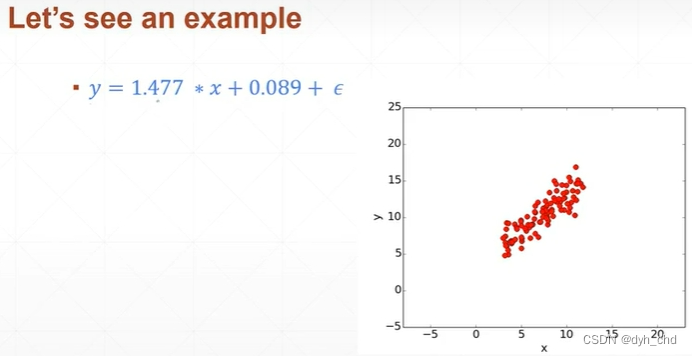
在这里插入图片描述
在已知w和b的取值，且有高斯噪声的情况下，x取[0,15]，生成100个数据点。

我们假设并不知道各参数值，只通过观察这一百组数据点，判断他们符合线性分布，现在求解w和b的参数，使得求得直线与各点整体的误差最小：
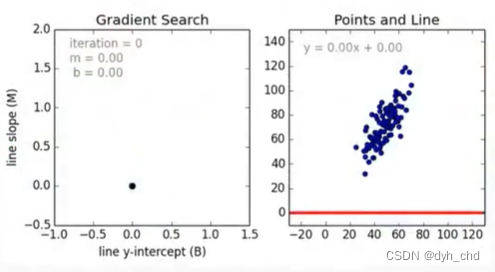
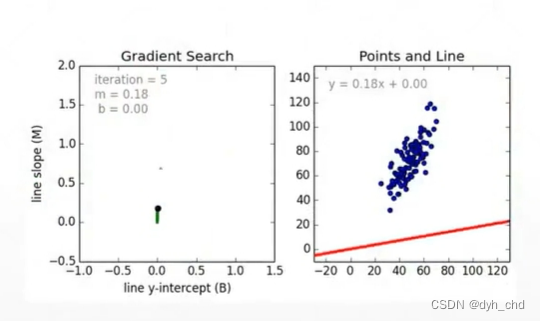
在这里插入图片描述

先将w,b都初始化为0，在每个点处对w和b求导，随着w，b的更新，最终近似解会接近理论值。

实战
在这里插入图片描述

其中，b`的计算跟w同理。loss将w和b分布当作自变量进行求导。

循环迭代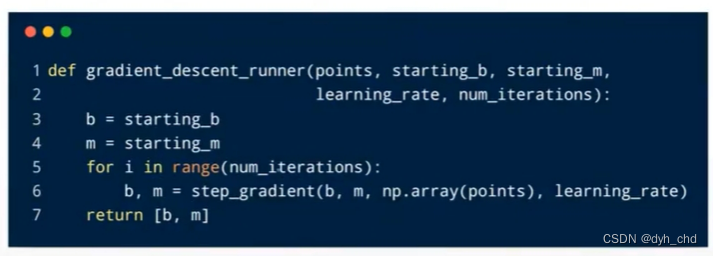
上代码：
先生成数据
再定义各计算函数
最终运行程序出结果

import numpy as np
import random
x = np.random.randint(low=5, high=15, size=100)
y = 1.47 * x + 0.089 + np.random.rand()
points = np.stack((x,y),1)
learningRate = 0.001
num = 10000
start_w = 0
start_b = 0def compute_error_for_line_given_points(w, b, points):totalError = 0for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]totalError += ((w * x + b) - y) ** 2return totalError / float(len(points))def step_gradient(w_current, b_current, points, learningRate):w_gradient = 0b_gradient = 0N = float(len(points))for i in range(len(points)):x = points[i, 0]y = points[i, 1]w_gradient += 2/N * x * (w_current * x + b_current - y)b_gradient += 2/N * (w_current * x + b_current - y)w_current -= learningRate * w_gradientb_current -= learningRate * b_gradientreturn w_current, b_currentdef gradient_descent_runner(points, starting_w, starting_b, learningRate, num):w = starting_wb = starting_bfor i in range(num):w, b = step_gradient(w, b, points, learningRate)return w, bif __name__ == '__main__':print('starting gradient descent at w = {0}, b = {1}, error = {2}'.format(start_w, start_b, compute_error_for_line_given_points(start_w, start_b, points)))print("Running...")w, b = gradient_descent_runner(points, start_w, start_b, learningRate, num)print("After {0} iterations, w = {1}, b = {2}, error = {3}".format(num, w, b, compute_error_for_line_given_points(w, b, points))结果：
D:\Anaconda\envs\ai_clone\python.exe D:/pyproject/torch/csdn1.pystarting gradient descent at w = 0, b = 0, error = 250.55349960186973
Running...
After 10000 iterations, w = 1.4856465608314946, b = 0.7776575796016487, error = 0.00216977834414222Process finished with exit code 0