💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 ：阿然成长日记 👈点击可跳转
📆 个人专栏： 🔹数据结构与算法🔹C语言进阶
🚩 不能则学，不知则问，耻于问人，决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍

一、二叉数的结构体

每一个节点有
1.数据域_data；
2.指向左子树的指针:_left
3.指向右子树的执指针：_right

typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;

二、构建二叉树，供后续测试使用

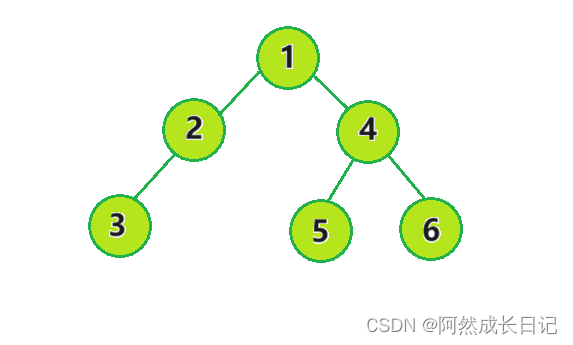
三、二叉树销毁

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);
}

四、构建节点

//构建节点BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}

五、二叉树的高度：

fmax函数的头文件：<math.h>
思路：每次选择左右子树中大的那一棵树，对其+1；

1.代码：

//树的高度int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->_left), TreeHeight(root->_right)) + 1;
}

2.测试结果：

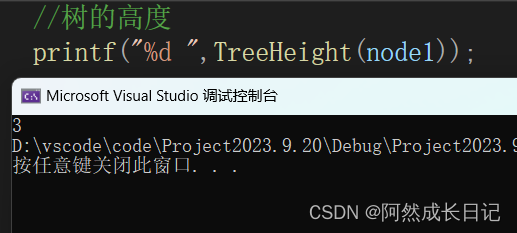
二叉树节点个数

思路：如果当前节点为NULL；则返回0；如果不是NULL；则向左右子树递归并+1；

1.代码：

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

2.测试结果：

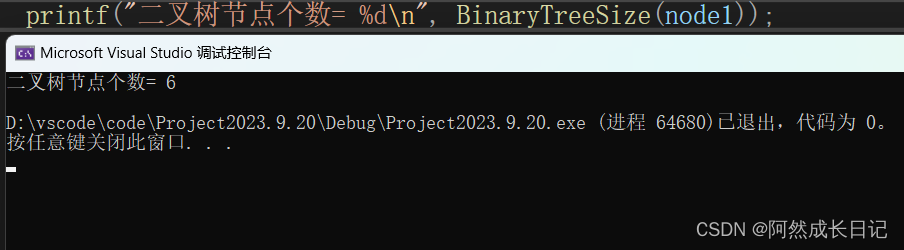
六、二叉树叶子节点个数

思路：
1.向下递归的条件是当前节点左或者右节点有一个为空，一个不为空。
2.当不满足下面的if语句时，就会return 左右两个节点，从而递归继续向下寻找叶子节点，
3.直到当前节点为空时，就停止返回0；或者找到叶子节点，返回1

1.代码：

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{//向下递归的条件是当前节点左或者右节点有一个为空，一个不为空。//当不满足下面的if语句时，就会return 左右两个节点，从而递归继续向下寻找叶子节点，//直到当前节点为空时，就停止返回0；或者找到叶子节点，返回1if (root == NULL)return 0;if (root->_left == NULL && root->_right == NULL)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

2.测试结果：

七、二叉树第k层节点个数

思路：
1.当找到第k==1，就返回1，意思是第k层个数+1；
2.当节点为空时，就结束向下递归，开始往回走。
3.如果不满足if条件，就继续向下递归。

1.代码：

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{//当找到第k==1，就返回1，意思是第k层个数+1；//当节点为空时，就结束向下递归，开始往回走。//如果不满足if条件，就继续向下递归。if (root == NULL)return 0;if (k == 1)return 1;return  BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

2.测试结果：

八、二叉树查找值为x的节点

思路;
1.当root==NULL时，说明当前子树中没有没有找到，返回NULL
2.当root->_data==x时，就return 当前节点，停止向下递归，开始向上回。
3.如果不满足上面两个if条件，就向下递归左，再右节点，
4.如果root->_data == x成立，返回的就不是空值通过if判断，并返回tmp。
5.在一次递归中，如果没有找到等于x的节点，和root=NULL两个条件时，就返回NULL；

1.代码：

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{//当root==NULL时，说明当前子树中没有没有找到，返回NULL//当root->_data==x时，就return 当前节点，停止向下递归，开始向上回。//如果不满足上面两个if条件，就向下递归左，再右节点，//如果root->_data == x成立，返回的就不是空值通过if判断，并返回tmp。//在一次递归中，如果没有找到等于x的节点，和root=NULL两个条件时，就返回NULL；if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* tmp = NULL;tmp=BinaryTreeFind(root->_left, x);if (tmp)return tmp;tmp = BinaryTreeFind(root->_right, x);if (tmp)return tmp;return NULL;
}

2.测试结果：

查询二叉树中节点值=3的节点。
查询

九、判断二叉树是否是完全二叉树

思路：
1.开始层序遍历，直到遇到NULL为止。
2.从遇到NULL的位置开始继续向下遍历，如果还能遇到非空节点，则说明不是完全二叉树。

1.代码：

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Que q;QueueInit(&q);//开始层序遍历，直到遇到NULL为止if (root)QueuePush(&q,root);while (!QueueEmpty(&q)){BTNode* tmp = QueueFront(&q);if (tmp == NULL)return false;QueuePush(&q,tmp->_left);QueuePush(&q,tmp->_right);QueuePop(&q);}//从遇到NULL的位置开始继续向下遍历，如果还能遇到非空节点，则说明不是完全二叉树。while (!QueueEmpty(&q)){BTNode* tmp = QueueFront(&q);QueuePop(&q);if (tmp != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

2.测试结果：

十、补充：队列代码

Queue.h

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Que;void QueueInit(Que* pq);
void QueueDestroy(Que* pq);
void QueuePush(Que* pq, QDataType x);
void QueuePop(Que* pq);
QDataType QueueFront(Que* pq);
QDataType QueueBack(Que* pq);
bool QueueEmpty(Que* pq);
int QueueSize(Que* pq);

Queue.c

#include "Queue.h"void QueueInit(Que* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}void QueueDestroy(Que* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;pq->size = 0;
}void QueuePush(Que* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->next = NULL;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}void QueuePop(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}pq->size--;
}QDataType QueueFront(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QDataType QueueBack(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}bool QueueEmpty(Que* pq)
{assert(pq);return pq->head == NULL;
}int QueueSize(Que* pq)
{assert(pq);return pq->size;
}