参考学习链接

计算机视觉与深度学习-04-图像去噪&卷积-北邮鲁鹏老师课程笔记

图像噪声

噪声点，其实在视觉上看上去让人感觉很难受，直观理解就是它跟周围的像素点差异比较大，显得比较突兀，视觉看起来很不舒服，这就是噪声点。

噪声分类

椒盐噪声

黑丝像素和白色像素随机出现

脉冲噪声

白色像素随机出现

对椒盐噪声&脉冲噪声去噪

使用高斯卷积核

高斯卷积核（低通滤波器）并不能去除椒盐噪声和脉冲噪声。

中值滤波器

中值滤波器是非线性操作。

刚开始的卷积核没有权重

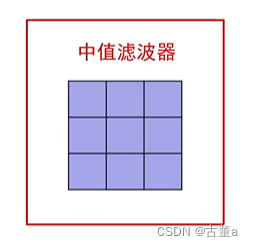
当图像处理时，将3 * 3的卷积核套在图像的9个像素上，取这9个图像向上的像素值，排序求出其中值，并用该中值替换当前中心点像素值。

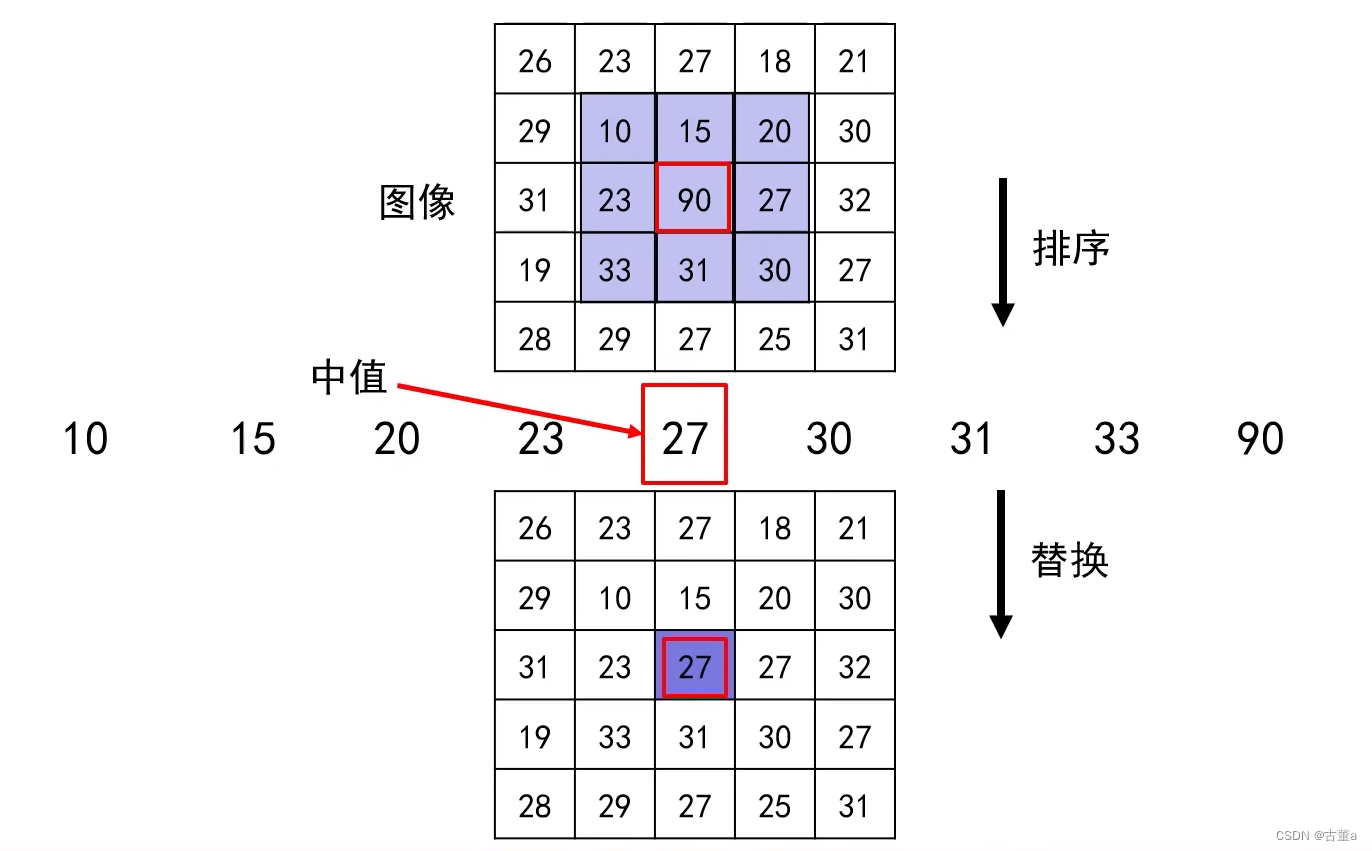
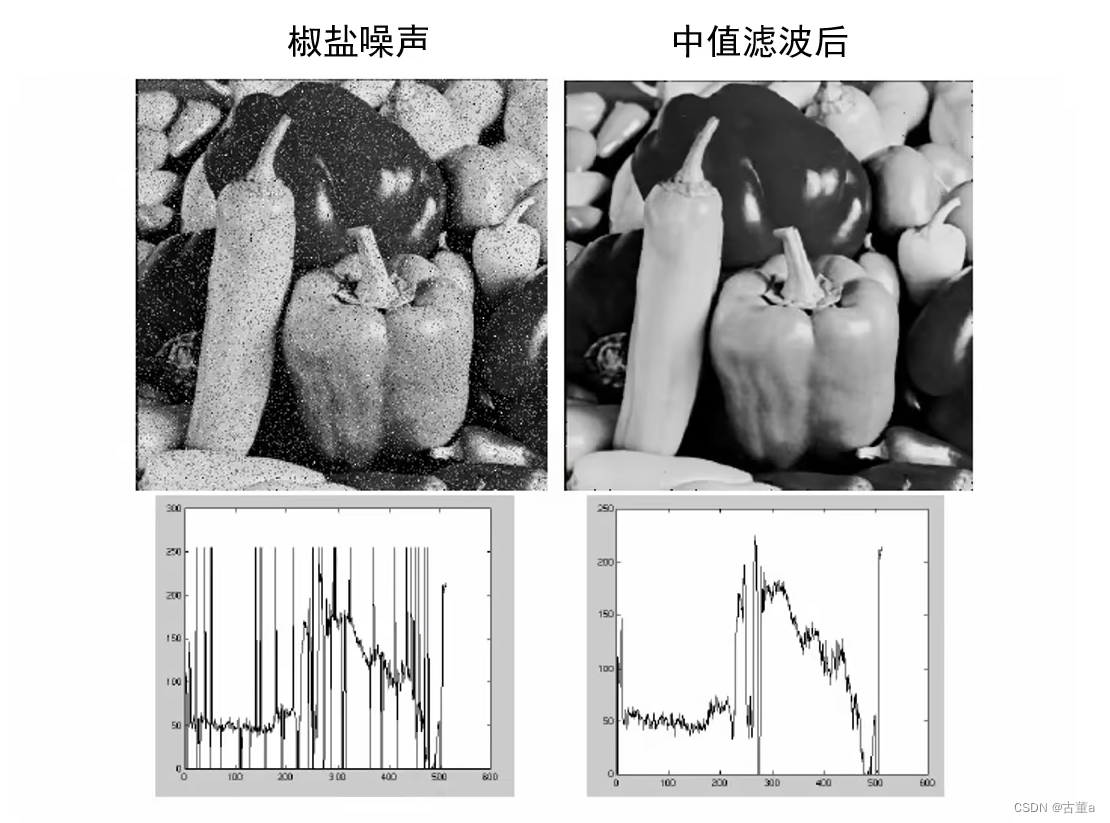
中值滤波对图像处理后

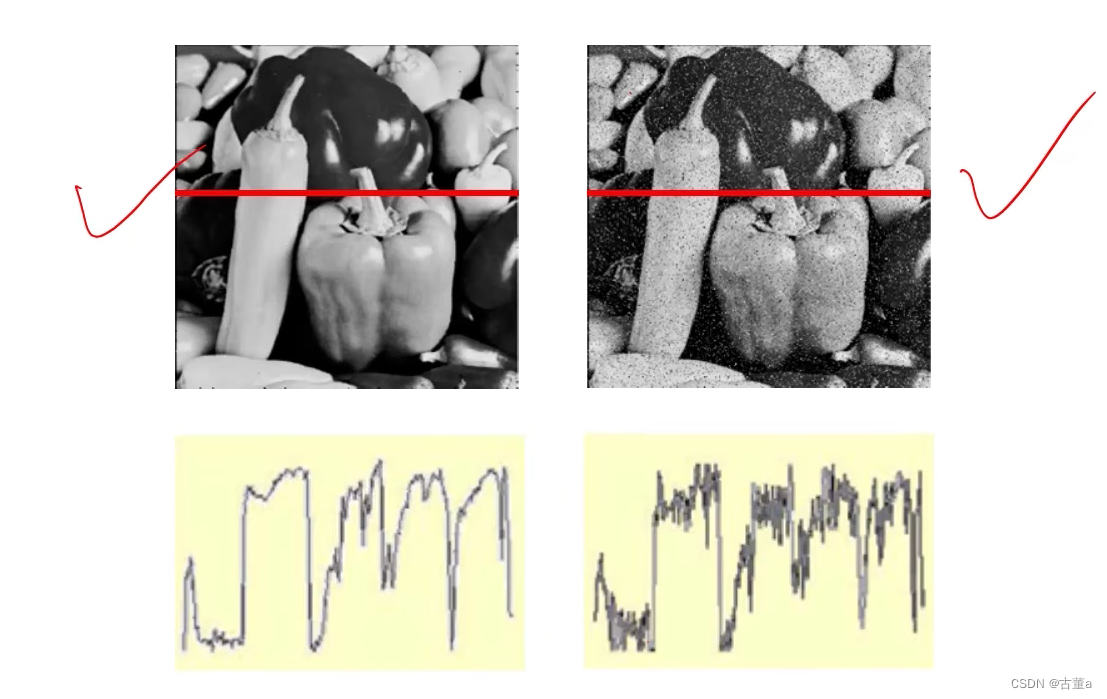
中值滤波 vs 均值滤波

• 中值滤波：卷积结果的像素值是图像原本就有这个像素值。
• 均值滤波：卷积结果的像素值是加权平均计算出的，可能原本并没有这个像素值。（高斯滤波）

高斯噪声

噪声强度变化服从高斯分布（正态分布）

高斯噪声数学模型是一个独立的加和模型$\hat{f}(x,y)=f(x,y)+\mu (x,y)$，一般认为$\eta (x,y)\sim N(\mu ,\sigma )$，通常μ = 0 , σ很小。

即认为 图像是由真实图像 + 高斯噪声组成的，高斯噪声的产生一个是由于采集器附加的噪声，另一个是由于光学问题带来的噪声。将两者合起来就是最终看到的带有噪声的图像。

因此对于高斯噪声就有了这样的假设：首先噪声的产生是相互独立的，而且服从均值为0的正态分布。

减少高斯噪声

噪声的方差越大，高斯卷积核的方差或尺寸就要越大。

虽然高斯卷积核可以去除高斯噪声，但是更模糊（最下图比最上图模糊），坏的噪声去掉了，好的像素也受到了影响。