课程地址和说明
线性代数实现p4
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
这节就算之前内容的复习,后面以截图形式呈现
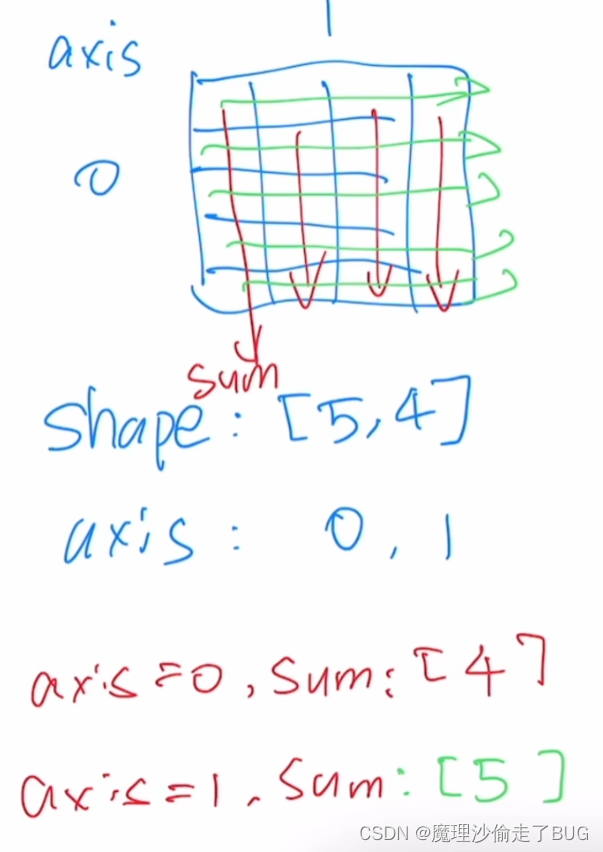
这节课就简单说明以下,axis为0是行,1是列,为0是每一列按行往下加和,为1就是每一行按列往下加和(SUM)

按某个维度求和就把某个维度去掉后求和
如果保留维度求和,就把要求和的那个维度设置为1,其他按照上面方法求和


2×5×4三维数组求和,先大致画个图:
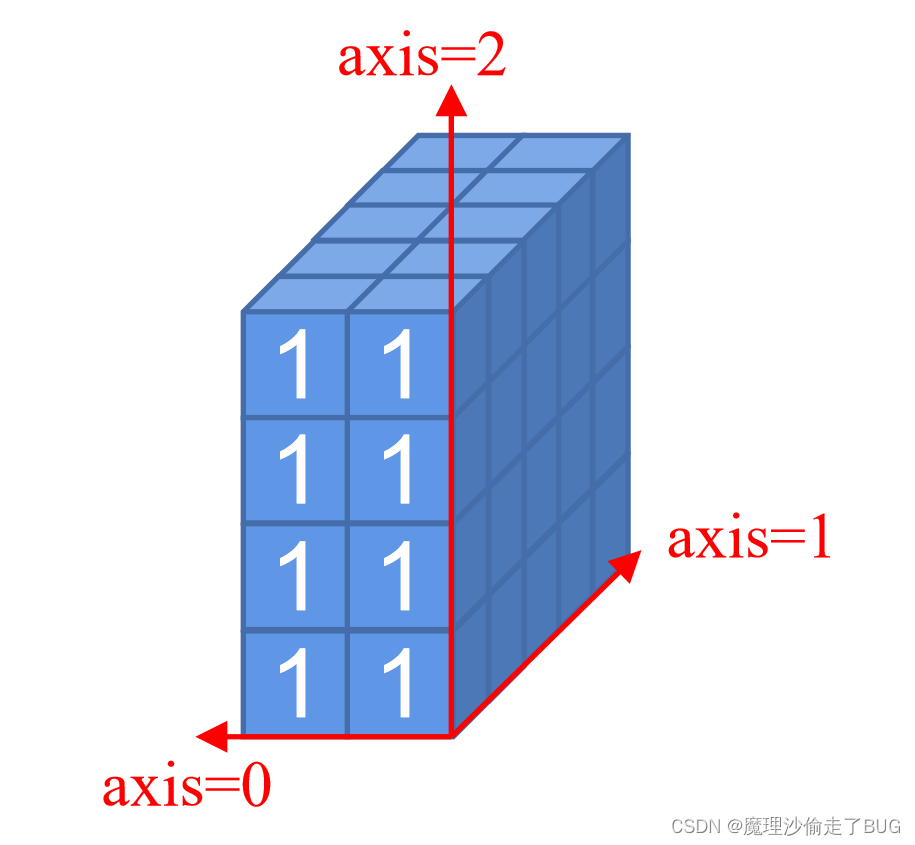
因为构建这个三维数组的时候,第一个维度设定为2,所以axis=0对应的是第一个维度2,其他以此类推。
- 假设对第一个维度(axis=0)求和,那么就是将其第一个维度方向加和,也就是如下的过程:
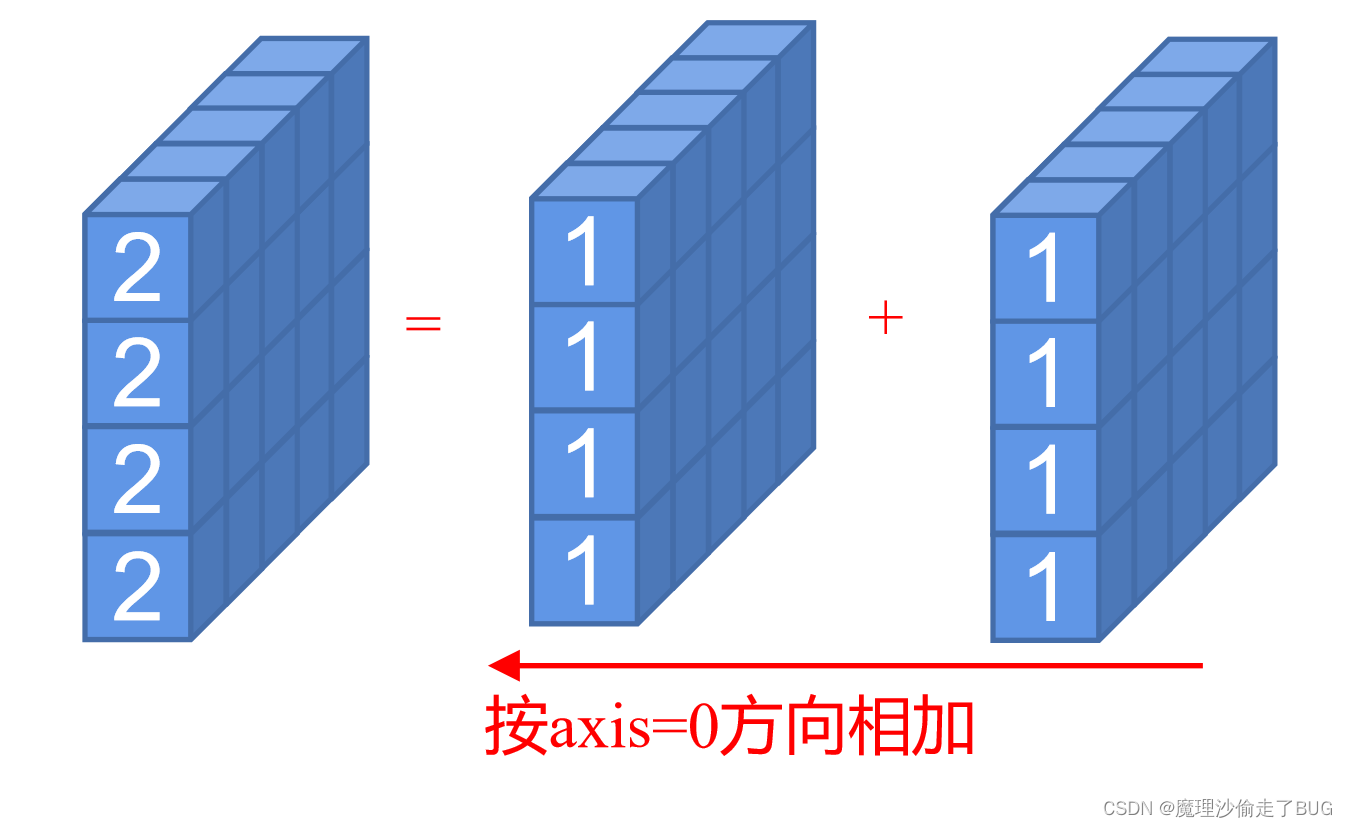
这样就能得到如下结果:
import torch
a =torch.ones((2,5,4))
print(a.sum(axis=0))
运行结果:
tensor([[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.]])
恰好为一个4×2全为2的矩阵。
- 假设对第二个维度(axis=1)求和,那么就是将其第二个维度方向加和,也就是如下的过程:
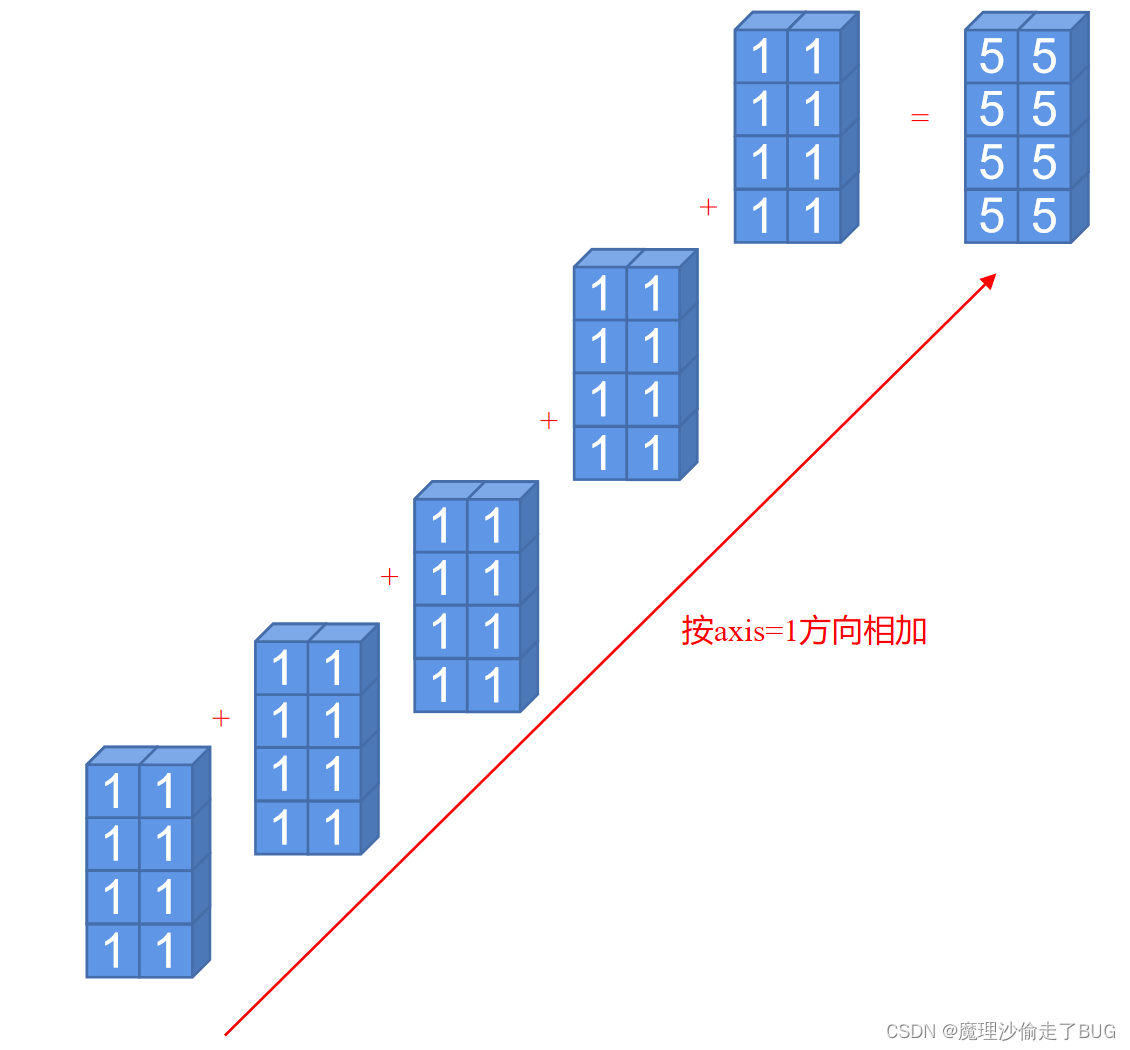
print(a.sum(axis=1))
运行结果:
tensor([[5., 5., 5., 5.],
[5., 5., 5., 5.]])
符合2×4且元素都为5的矩阵
- 假设对第三个维度(axis=2)求和,那么就是将其第三个维度方向加和,也就是如下的过程:
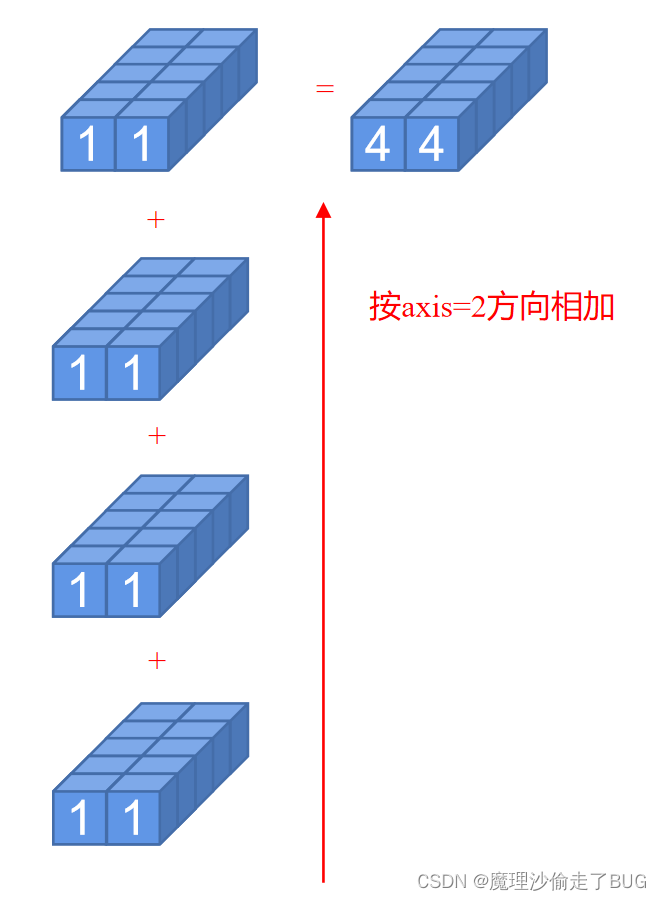
print(a.sum(axis=2))
运行结果:
tensor([[4., 4., 4., 4., 4.],
[4., 4., 4., 4., 4.]])
- 对第一和第二两个维度合并求和,即如下过程:

print(a.sum(axis=[0,1]))
运行结果:
tensor([10., 10., 10., 10.])
正如上图所示,是一个一维向量
下面就是上面所说的实现,除了三维的这个求和,其他都比较简单: