原文链接:http://tecdat.cn/?p=23236
在频率学派中,观察样本是随机的,而参数是固定的、未知的数量(点击文末“阅读原文”获取完整代码数据)。
相关视频
什么是频率学派?
概率被解释为一个随机过程的许多观测的预期频率。
有一种想法是 "真实的",例如,在预测鱼的生活环境时,盐度和温度之间的相互作用有一个回归系数?
什么是贝叶斯学派?
在贝叶斯方法中,概率被解释为对信念的主观衡量。
所有的变量--因变量、参数和假设都是随机变量。我们用数据来确定一个估计的确定性(可信度)。
这种盐度X温度的相互作用反映的不是绝对的,而是我们对鱼的生活环境所了解的东西(本质上是草率的)。
目标
频率学派
保证正确的误差概率,同时考虑到抽样、样本大小和模型。
缺点:需要对置信区间、第一类和第二类错误进行复杂的解释。
优点:更具有内在的 "客观性 "和逻辑上的一致性。
贝叶斯学派
分析更多的信息能在多大程度上提高我们对一个系统的认识。
缺点:这都是关于信仰的问题! ...有重大影响。
优点: 更直观的解释和实施,例如,这是这个假设的概率,这是这个参数等于这个值的概率。可能更接近于人类自然地解释世界的方式。
实际应用中:为什么用贝叶斯
具有有限数据的复杂模型,例如层次模型,其中
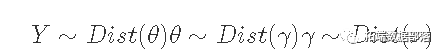
实际的先验知识非常少
贝叶斯法则:
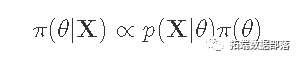
一些典型的贝叶斯速记法。
注意:
贝叶斯的最大问题在于确定先验分布。先验应该是什么?它有什么影响?
目标:
计算参数的后验分布:π(θ|X)。
点估计是后验的平均值。
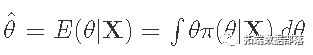
一个可信的区间是

你可以把它解释为一个参数在这个区间内的概率 。
计算
皮埃尔-西蒙-拉普拉斯(1749-1827)(见:Sharon Bertsch McGrayne: The Theory That Would Not Die)
有些问题是可分析的,例如二项式似然-贝塔先验。
但如果你有很多参数,这是不可能完成的操作
如果你有几个参数,而且是奇数分布,你可以用数值乘以/整合先验和似然(又称网格近似)。
尽管该理论可以追溯到1700年,甚至它对推理的解释也可以追溯到19世纪初,但它一直难以更广泛地实施,直到马尔科夫链蒙特卡洛技术的发展。
MCMC
MCMC的思想是对参数值θi进行 "抽样"。
回顾一下,马尔科夫链是一个随机过程,它只取决于它的前一个状态,而且(如果是遍历的),会生成一个平稳的分布。
技巧 "是找到渐进地接近正确分布的抽样规则(MCMC算法)。
有几种这样的(相关)算法。
Metropolis-Hastings抽样
Gibbs 抽样
No U-Turn Sampling (NUTS)
Reversible Jump
一个不断发展的文献和工作体系!
Metropolis-Hastings 算法
开始:
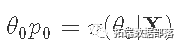
跳到一个新的候选位置:

计算后验:

如果
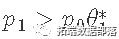
如果
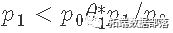
转到第2步
Metropolis-Hastings: 硬币例子
你抛出了5个正面。你对θ的最初 "猜测 "是
MCMC:
p.old <- prior *likelihood
while(length(thetas) <= n){theta.new <- theta + rnorm(1,0,0.05)p.new <- prior *likelihood if(p.new > p.old | runif(1) < p.new/p.old){theta <- theta.newp.old <- p.new}画图:
hist(thetas\[-(1:100)\] )
curve(6*x^5 )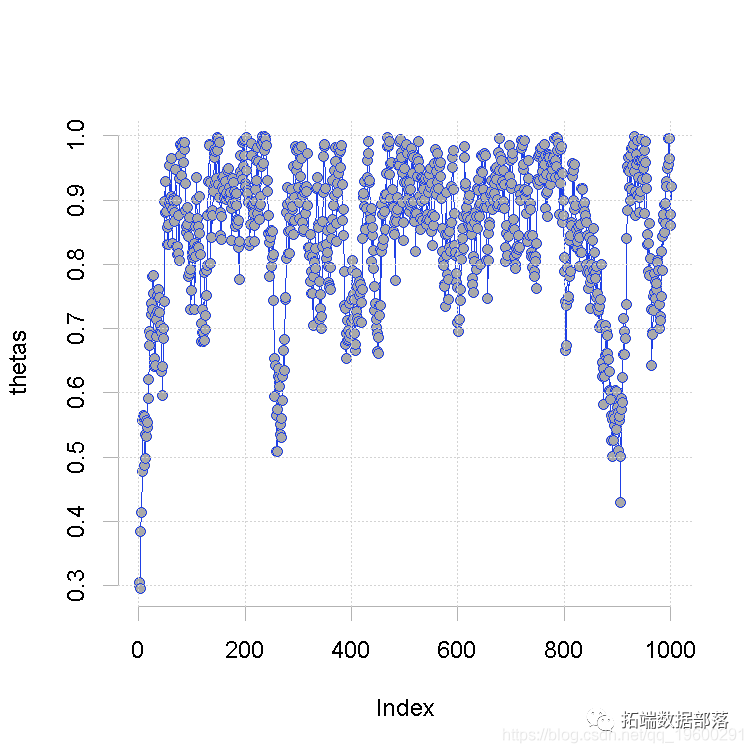

点击标题查阅往期内容

R语言用贝叶斯线性回归、贝叶斯模型平均 (BMA)来预测工人工资

左右滑动查看更多

01

02

03

04

采样链:调整、细化、多链

那个 "朝向 "平稳的初始过渡被称为 "预烧期",必须加以修整。
怎么做?用眼睛看
采样过程(显然)是自相关的。
如何做?通常是用眼看,用acf()作为指导。
为了保证你收敛到正确的分布,你通常会从不同的位置获得多条链(例如4条)。
有效样本量
MCMC 诊断法
R软件包帮助分析MCMC链。一个例子是线性回归的贝叶斯拟合(α,β,σ
plot(line)
预烧部分:
plot(line\[\[1\]\], start=10)
MCMC诊断法
查看后验分布(同时评估收敛性)。
density(line)
参数之间的关联性,以及链内的自相关关系
levelplot(line\[\[2\]\])
acfplot(line)

统计摘要

运行MCMC的工具(在R内部)
逻辑Logistic回归:婴儿出生体重低
logitmcmc(low~age+as.factor(race)+smoke )
plot(mcmc)
MCMC与GLM逻辑回归的比较


MCMC与GLM逻辑回归的比较
对于这个应用,没有很好的理由使用贝叶斯建模,除非--你是 "贝叶斯主义者"。你有关于回归系数的真正先验信息(这基本上是不太可能的)。
一个主要的缺点是 先验分布棘手的调整参数。
但是,MCMC可以拟合的一些更复杂的模型(例如,层次的logit MCMChlogit)。
Metropolis-Hastings

Metropolis-Hastings很好,很简单,很普遍。但是对循环次数很敏感。而且可能太慢,因为它最终会拒绝大量的循环。
Gibbs 采样

在Gibbs吉布斯抽样中,你不是用适当的概率接受/拒绝,而是用适当的条件概率在参数空间中行进。并从该分布中抽取一次。
然后你从新的条件分布中抽取下一个参数。
比Metropolis-Hastings快得多。有效样本量要高得多!
BUGS(OpenBUGS,WinBUGS)是使用吉布斯采样器的贝叶斯推理。
JAGS是 "吉布斯采样器"
其他采样器
汉密尔顿蒙特卡洛(HMC)--是一种梯度的Metropolis-Hastings,因此速度更快,对参数之间的关联性更好。
No-U Turn Sampler(NUTS)--由于不需要固定的长度,它的速度更快。这是STAN使用的方法(见http://arxiv.org/pdf/1111.4246v1.pdf)。

(Hoffman and Gelman 2011)
其他工具
你可能想创建你自己的模型,使用贝叶斯MC进行拟合,而不是依赖现有的模型。为此,有几个工具可以选择。
BUGS / WinBUGS / OpenBUGS (Bayesian inference Using Gibbs Sampling) - 贝叶斯抽样工具的鼻祖(自1989年起)。WinBUGS是专有的。OpenBUGS的支持率很低。
JAGS(Just Another Gibbs Sampler)接受一个用类似于R语言的语法编写的模型字符串,并使用吉布斯抽样从这个模型中编译和生成MCMC样本。可以在R中使用rjags包。
Stan(以Stanislaw Ulam命名)是一个类似于JAGS的相当新的程序--速度更快,更强大,发展迅速。从伪R/C语法生成C++代码。安装:http://mc-stan.org/rstan.html**
Laplace’s Demon 所有的贝叶斯工具都在R中:http://www.bayesian-inference.com/software
STAN
要用STAN拟合一个模型,步骤是:
为模型生成一个STAN语法伪代码(在JAGS和BUGS中相同
运行一个R命令,用C++语言编译该模型
使用生成的函数来拟合你的数据
STAN示例--线性回归
STAN代码是R(例如,具有分布函数)和C(即你必须声明你的变量)之间的一种混合。每个模型定义都有三个块。
_1_.数据块:
int n; //vector\[n\] y; // Y 向量这指定了你要输入的原始数据。在本例中,只有Y和X,它们都是长度为n的(数字)向量,是一个不能小于0的整数。
_2_. 参数块
real beta1; // slope这些列出了你要估计的参数:截距、斜率和方差。
_3_. 模型块
sigma ~ inv_gamma(0.001, 0.001); yhat\[i\] <- beta0 + beta1 * (x\[i\] - mean(x));}y ~ normal(yhat, sigma);注意:
你可以矢量化,但循环也同样快
有许多分布(和 "平均值 "等函数)可用
请经常参阅手册!https://github.com/stan-dev/stan/releases/download/v2.9.0/stan-reference-2.9.0.pdf
2. 在R中编译模型
你把你的模型保存在一个单独的文件中, 然后用stan_model()命令编译这个模型。
这个命令是把你描述的模型,用C++编码和编译一个NUTS采样器。相信我,自己编写C++代码是一件非常非常痛苦的事情(如果没有很多经验的话),而且它保证比R中的同等代码快得多。
注意:这一步可能会很慢。
3. 在R中运行该模型
这里的关键函数是sampling()。还要注意的是,为了给你的模型提供数据,它必须是列表的形式
模拟一些数据。
X <- runif(100,0,20)
Y <- rnorm(100, beta0+beta1*X, sigma)进行取样!
sampling(stan, Data)这里有大量的输出,因为它计算了
print(fit, digits = 2)
MCMC诊断法
为了应用coda系列的诊断工具,你需要从STAN拟合对象中提取链,并将其重新创建为mcmc.list。
extract(stan.fit
alply(chains, 2, mcmc)

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例》。
点击标题查阅往期内容
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
PYTHON银行机器学习:回归、随机森林、KNN近邻、决策树、高斯朴素贝叶斯、支持向量机SVM分析营销活动数据|数据分享
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
MATLAB随机森林优化贝叶斯预测分析汽车燃油经济性
R语言中贝叶斯网络(BN)、动态贝叶斯网络、线性模型分析错颌畸形数据
使用贝叶斯层次模型进行空间数据分析
MCMC的rstan贝叶斯回归模型和标准线性回归模型比较
python贝叶斯随机过程:马尔可夫链Markov-Chain,MC和Metropolis-Hastings,MH采样算法可视化
Python贝叶斯推断Metropolis-Hastings(M-H)MCMC采样算法的实现
matlab贝叶斯隐马尔可夫hmm模型实现
贝叶斯线性回归和多元线性回归构建工资预测模型
Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据
R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据
R语言STAN贝叶斯线性回归模型分析气候变化影响北半球海冰范围和可视化检查模型收敛性
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据
R语言JAGS贝叶斯回归模型分析博士生延期毕业完成论文时间
R语言Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
Python决策树、随机森林、朴素贝叶斯、KNN(K-最近邻居)分类分析银行拉新活动挖掘潜在贷款客户
R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断
R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数
随机森林优化贝叶斯预测分析汽车燃油经济性
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数
R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归
Python贝叶斯回归分析住房负担能力数据集
R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析
Python用PyMC3实现贝叶斯线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
R语言Gibbs抽样的贝叶斯简单线性回归仿真分析
R语言和STAN,JAGS:用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言贝叶斯线性回归和多元线性回归构建工资预测模型
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言stan进行基于贝叶斯推断的回归模型
R语言中RStan贝叶斯层次模型分析示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
WinBUGS对多元随机波动率模型:贝叶斯估计与模型比较
R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
视频:R语言中的Stan概率编程MCMC采样的贝叶斯模型
R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计

![]()