全文链接：http://tecdat.cn/?p=24492

此分析的目的是构建一个过程，以在给定时变波动性的情况下正确估计风险价值。风险价值被广泛用于衡量金融机构的市场风险。我们的时间序列数据包括 1258 天的股票收益（点击文末“阅读原文”获取完整代码数据）。

介绍

为了解释每日收益率方差的一小部分，我们使用 Box-Jenkins 方法来拟合自回归综合移动平均 (ARIMA) 模型，并测试带下划线的假设。稍后，当我们寻找替代方案、最佳拟合分布形式时，我们会检查收益率的正态性。我们使用广义自回归异方差 (GARCH) 方法估计残差的条件方差，并将其与 delta-normal 方法进行比较。

相关视频

数据

出于建模过程的目的，我们每天收集了 5 年（2013 年 2 月至 2018 年 2 月）的花旗公司股票（共 1259 个观察样本）。

# 加载库
library(tidyverse)# 加载数据read.csv('stock.csv', header = T)# 每只股票一栏plot( y = stok$C , geo = 'line')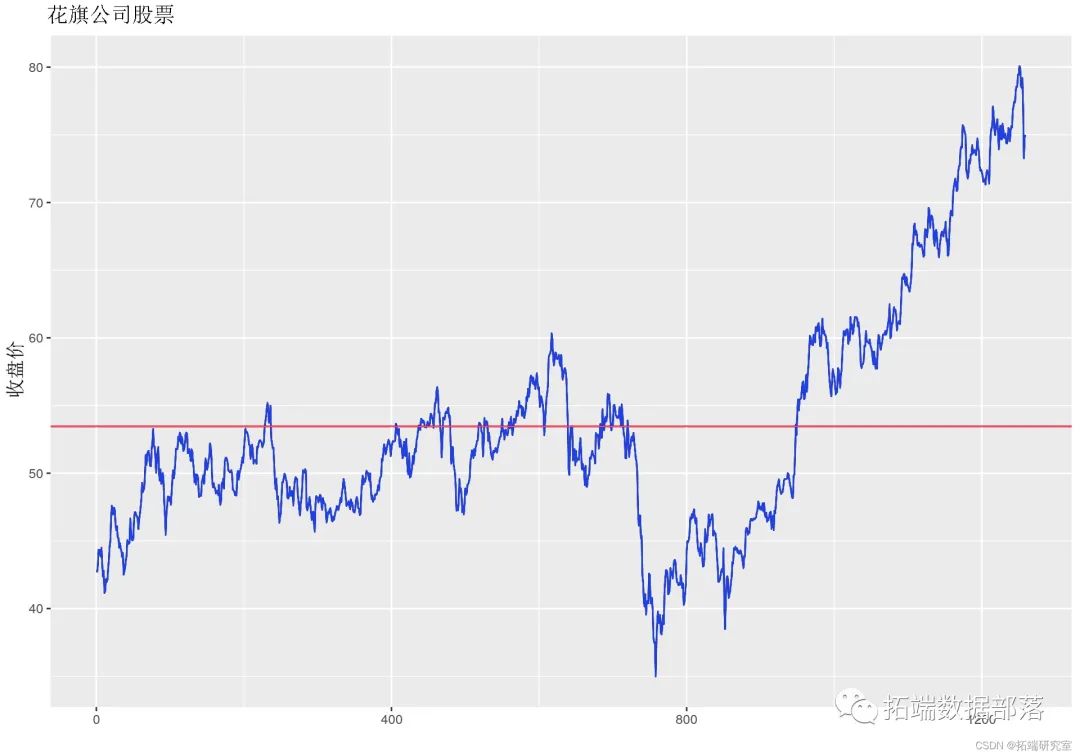

红线表示此特定时间范围内的平均收盘价。

非平稳过程具有随时间变化的均值、方差和协方差。使用非平稳时间序列数据会导致预测不可靠。平稳过程是均值回归的，即它在具有恒定方差的恒定均值附近波动。在我们的例子中，平稳性是指平稳时间序列满足三个条件的弱平稳性：

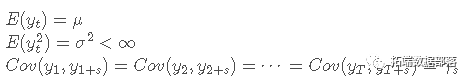
为了解决这个问题，我们主要使用差分法。一阶差分可以描述为

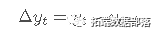
对于平稳性变换，我们更倾向于计算简单的日收益，表示如下

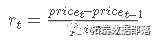
ret = diff(stoks$C) / socs$C\[-legth\]plot(x = 1:length, y = res )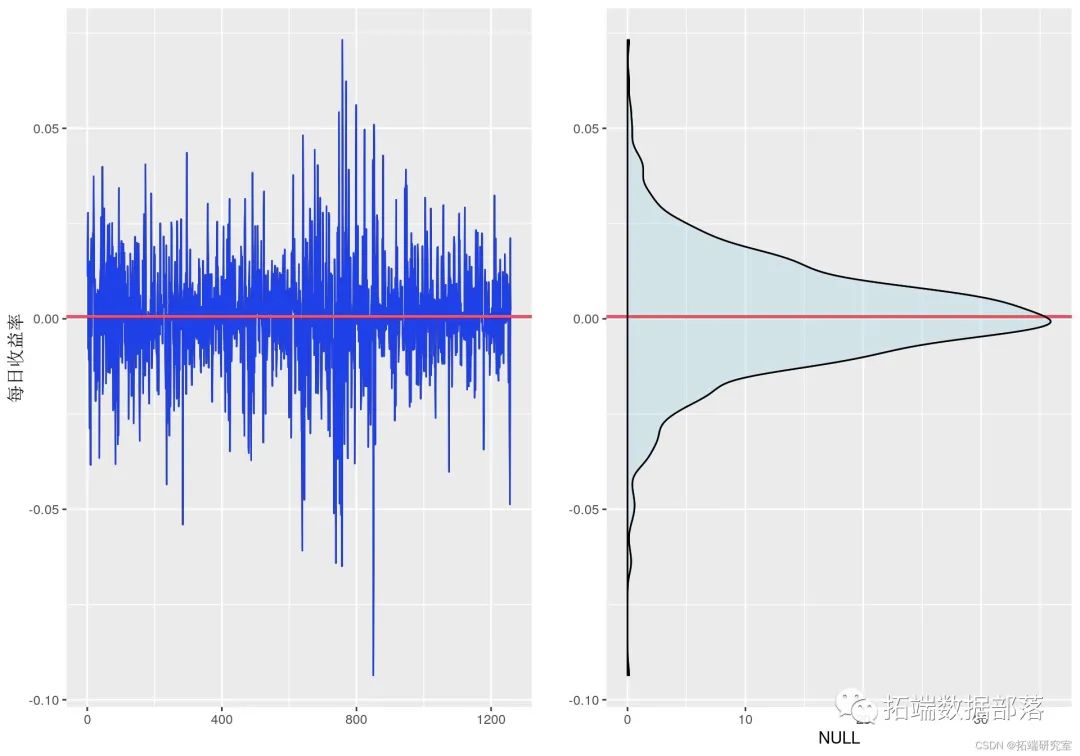

为了验证收益率的平稳性，我们使用了 Dickey-Fuller 检验，其中零假设表示非平稳时间序列。

---

点击标题查阅往期内容

Python计算股票投资组合的风险价值（VaR）

左右滑动查看更多

01

02

03

04

adf.test(ret)

小的 P 值 (<0.01) 表明有足够的证据拒绝原假设，因此时间序列被认为是平稳的。

Box-Jenkins 方法

对于时间序列分析，Box-Jenkins 方法应用 ARIMA 模型来找到代表生成时间序列的随机过程的时间序列模型的最佳拟合。该方法使用三阶段建模方法：a) 识别，b) 估计，c) 诊断检查。

识别

要使用 Box-Jenkins 方法，我们必须确保时间序列是平稳的。在我们的例子中，我们使用我们在前一部分中已经检查过平稳性的股票的收益率。此外，基于自相关函数 (ACF) 和偏自相关函数 (PACF)，可以确定 ARIMA 模型的 p、d 和 q 阶。识别模型的另一种方法是 Akaike 信息准则 (AICc)。AIC 估计每个模型相对于其他每个模型的质量。

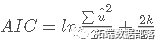
其中

• ∑u^2= 残差平方和

• T = 观察次数

• k = 模型参数的数量 (p + q + 1)

很明显，当模型中加入额外的滞后参数时，残差总和会减少，但可能会出现过拟合的问题。AIC 处理过拟合和欠拟合的风险。将选择 AIC 最低的模型。

auto.arima(rets )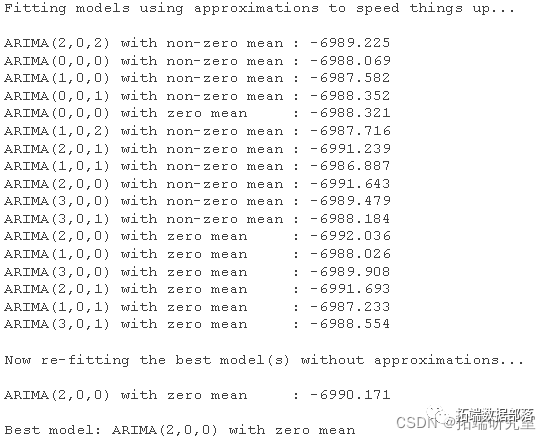

可以通过上面的过程观察到我们计算了各种 ARIMA 模型的 AIC ，并且我们推断出合适的模型是 二阶自回归 (AR(2))。

估计

为了估计参数的系数，我们使用最大似然。使用ARIMA(2, 0, 0)作为选择模型，结果如下：

model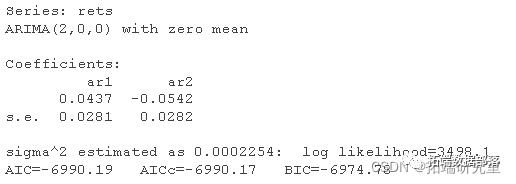

因此，该过程可以描述为：

rt=0.0437∗rt−1−0.0542∗rt−2+ϵt 其中 ϵt 是白噪声

诊断检查

该程序包括观察残差图及其 ACF & PACF 图，并检查 Ljung-Box 测试结果。如果模型残差的 ACF 和 PACF 没有显示显着滞后，则所选模型是合适的。

ggtsdisplay(plot)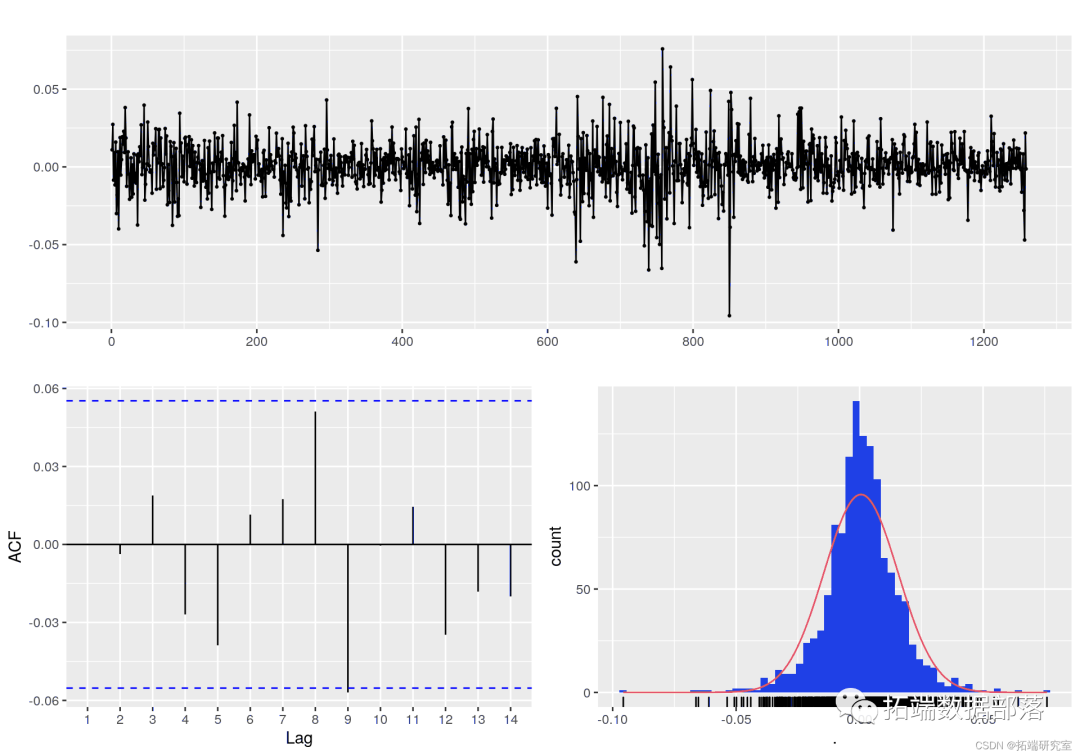

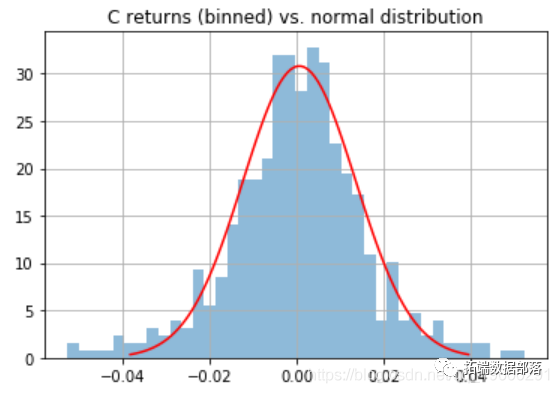
ACF 和 PACF 图很相似，自相关似乎为零。右下角图表示残差与正态分布 N(0, σ2σ2) 相比的直方图。

为了进一步检验残差不相关的假设，我们执行 Ljung-Box 检验。

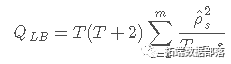
QLB统计量不对称地遵循具有 mpq 自由度的 X2 分布。零假设是指 H0:ρ1=ρ2=⋯=ρm=0

Box.test(resiuas)

我们不能拒绝原假设，因此残差的过程表现得像白噪声，所以没有可能被建模。

GARCH 实现

尽管残差的 ACF 和 PACF 没有显着滞后，但残差的时间序列图显示出一些集群波动。重要的是要记住，ARIMA 是一种对数据进行线性建模的方法，并且预测宽度保持不变，因为该模型不会反映最近的变化或包含新信息。为了对波动性进行建模，我们使用自回归条件异方差 (ARCH) 模型。ARCH 是时间序列数据的统计模型，它将当前误差项的方差描述为先前时间段误差项实际大小的函数。

我们假设感兴趣的时间序列 rtrt 被分解为两部分，可预测和不可预测部分，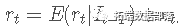

其中 It−1 是时间 t−1 的信息集，并且 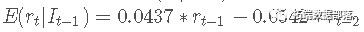 ϵt 是不可预测的部分。

不可预测的成分，可以表示为以下形式的 GARCH 过程：

其中 zt 是一个均值为零且方差等于 1 的独立同分布随机变量序列。ϵt的条件方差是 σt，它是时间 t−1信息集的时变函数。

下一步是定义误差项分解的第二部分，即条件方差 σt。对于这样的任务，我们可以使用 GARCH(1, 1) 模型，表示为：

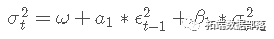
当残差平方相关时，GARCH 过程有效。ACF 和 PACF 图清楚地表明显着相关性。

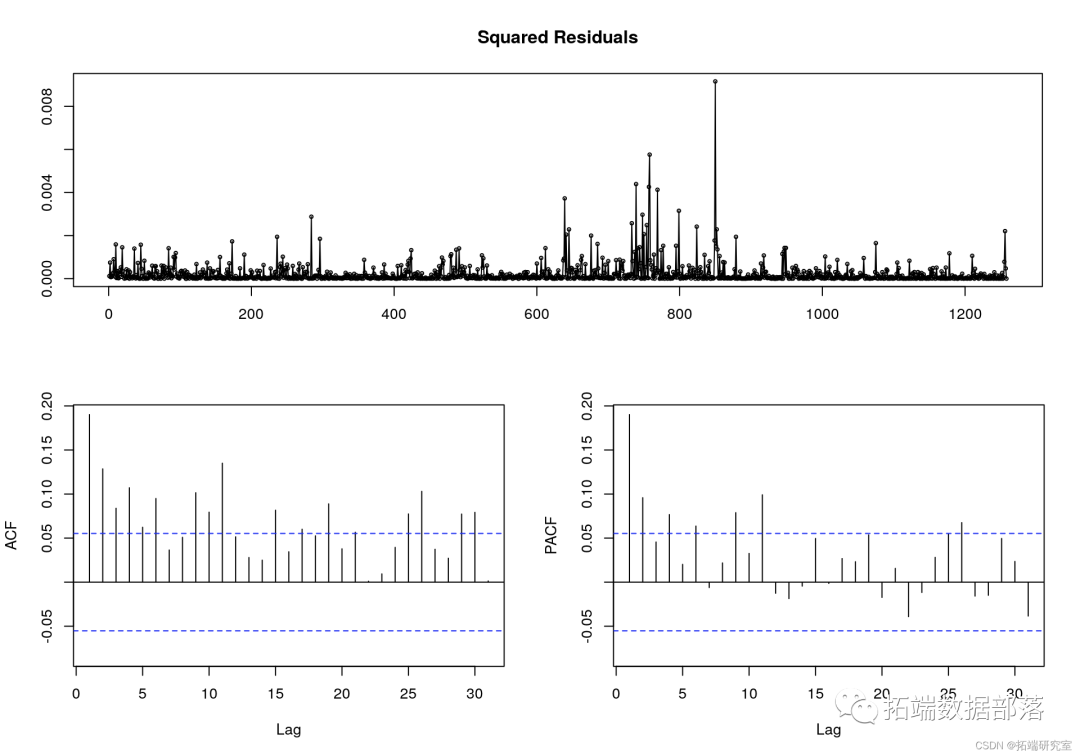
另一种检验平方残差异方差性的方法是对 a1 和 β1参数进行显着性检验。

#模型定义
ugarchpec(varin , mean.model fit(sec = model.spec ')

a1和 β1都显着不同于零，因此假设残差随时间变化的波动率是合理的。

σt−12 项的连续替换，GARCH 方程可以写为：

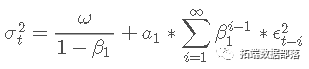
当我们用优化给出的系数估计替换时，我们得到以下等式：

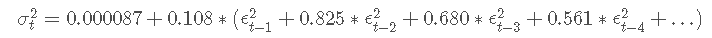
鉴于 0<β1<1，随着滞后的增加，残差平方的影响减小。

风险价值

风险价值（VaR）是一种基于当前头寸的下行风险的统计量度。它估计在正常的市场条件下，一组投资在设定的时间段内可能会有多少损失。 

VaR 统计具有三个组成部分：a) 时间段，b) 置信水平，c) 损失金额（或损失百分比）。对于 95% 的置信水平，我们可以说最坏的每日损失不会超过 VaR 估计。如果我们使用历史数据，我们可以通过取 5% 的分位数值来估计 VaR。对于我们的数据，这个估计是：

quante(res , 0.05)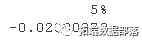

qplot(ret)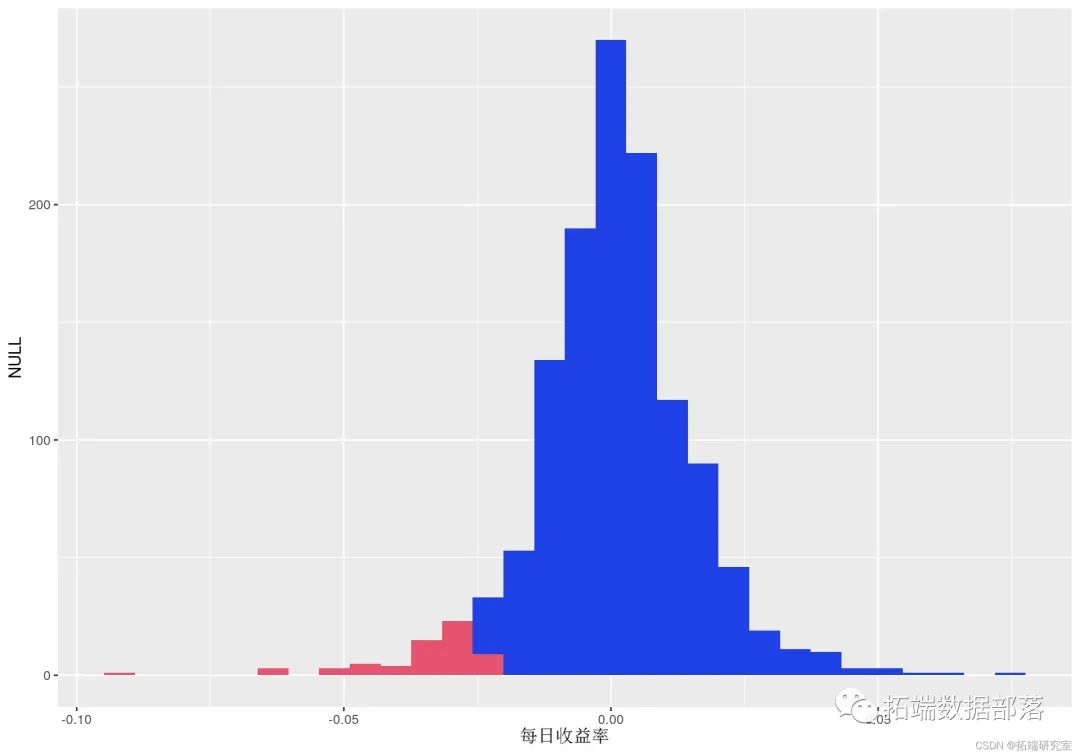

红色条表示低于 5% 分位数的收益率。

分布特征

为了估计 VaR，我们需要正确定义假设分布的相应分位数。对于正态分布，对应于 a = 5% 的分位数为 -1.645。经验证据表明，正态性假设通常会产生较弱的结果。Jarque-Bera 检验可以检验股票收益服从正态分布的假设。

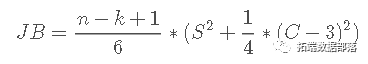
其中 S 是偏度，C 是峰度。正态分布样本将返回JB 分数。低 p 值表明股票收益不是正态分布的。

ja.tst(rets)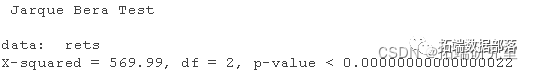

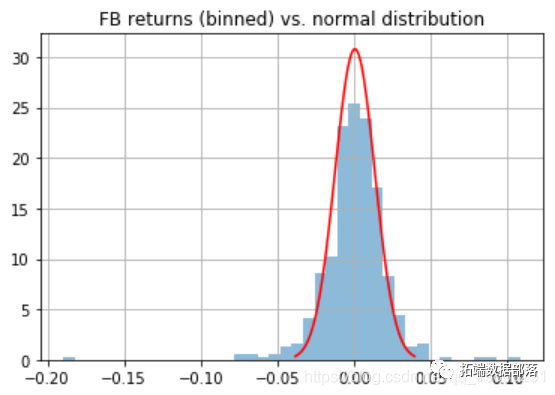
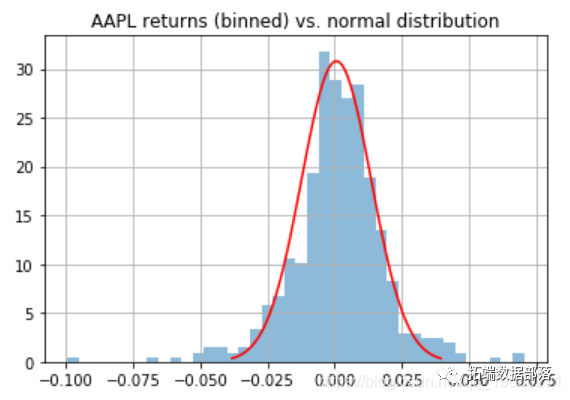
qplot(ret , gom = 'desity') + geom_density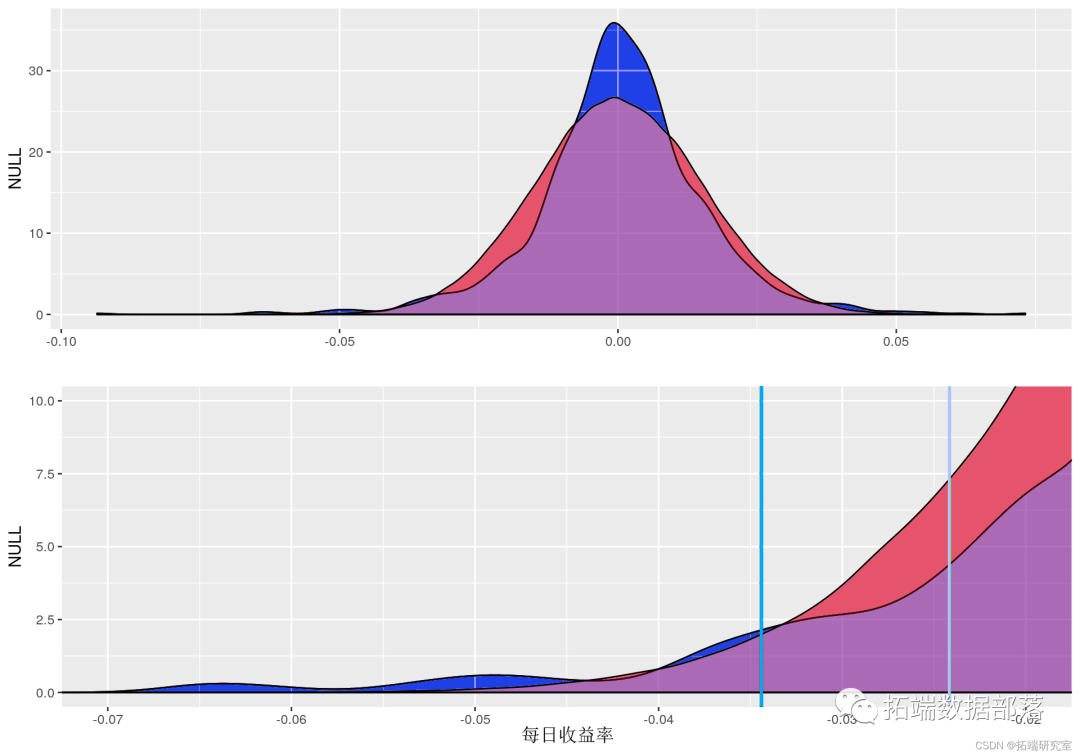

在上图中，显示了股票收益（_蓝色_）和正态分布数据（_红色_）的密度图。下图的垂直线代表 a = 0.05（_浅绿色_）和 a = 0.01（_深绿色_）的正常对应分位数。下图表明对于 95% 的显着性，使用正态分布可能会高估风险值。但是，对于 99% 的显着性水平，正态分布会低估风险。

学生的 t 分布

为了更充分地模拟尾部的厚度，我们可以对股票收益使用其他分布假设。t 分布是对称的钟形分布，就像正态分布一样，但尾部较重，这意味着它更容易产生远离其均值的值。我们使用_rugarch 包中_的 fitdist 函数  来获取 t 分布的拟合参数。

fitdispars

cat("对于 a = 0.05，正态分布的分位数值为：" ,qnorm(p = 0.05) , "\\n" ,
)

正如我们所观察到的，95% 显着性水平的分位数表明正态分布高估了风险，但 99% 未能发现异常值的存在，因此发生了对风险的低估。

Garch VaR 和Delta-normal 方法

Delta-normal 方法假设所有股票收益都是正态分布的。这种方法包括回到过去并计算收益的方差。风险价值可以定义为：

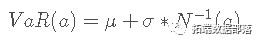
其中 μ 是平均股票收益，σ 是收益的标准差，a 是选定的置信水平，N−1 是逆 PDF 函数，生成给定 a 的正态分布的相应分位数。

这种简单模型的结果常常令人失望，如今很少在实践中使用。正态性和恒定每日方差的假设通常是错误的，我们的数据也是如此。

之前我们观察到收益率表现出随时间变化的波动性。因此，对于 VaR 的估计，我们使用 GARCH(1,1) 模型给出的条件方差。我们使用学生的 t 分布。对于此方法，风险价值表示为：

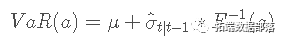
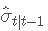 是给定 t−1 信息的条件标准偏差，并且  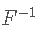是 t 分布的逆 PDF 函数。

qplot(y = rets , gom = 'point') + gem_pnt(col = 'lihtgrson')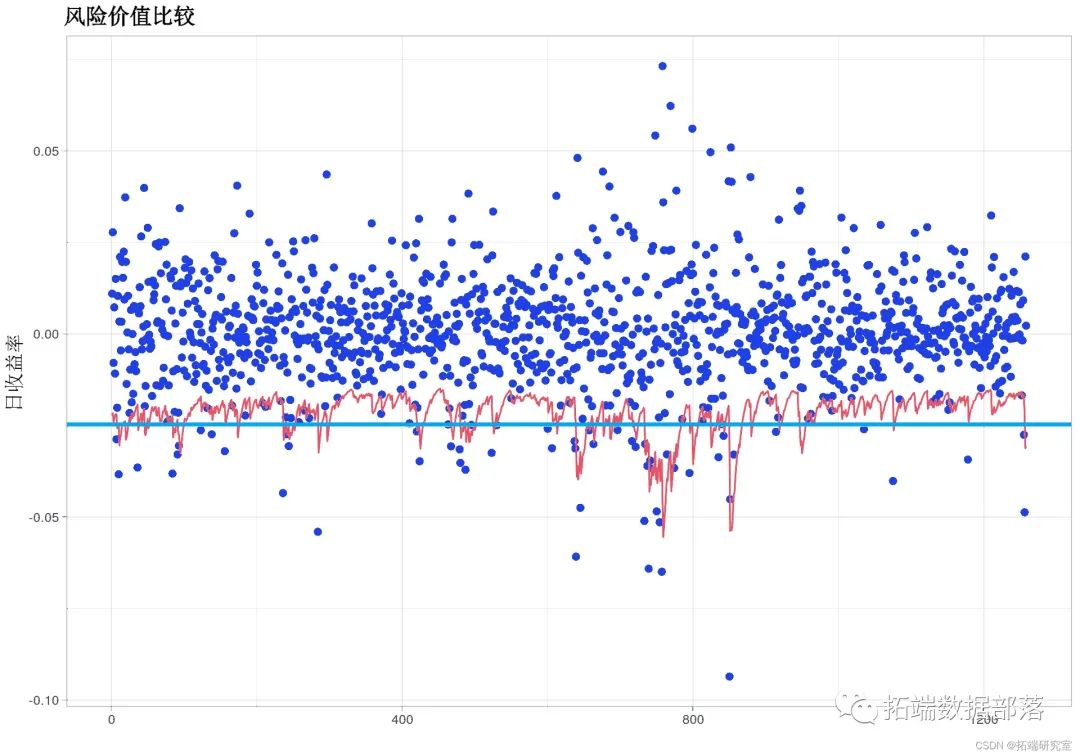

红线表示 GARCH 模型产生的 VaR，蓝线表示 delta-normal VaR。

VaR预测

该 ugarchroll 方法允许执行的模型/数据集组合的滚动估计和预测。它返回计算预测密度的任何所需度量所需的分布预测参数。我们将最后 500 个观测值设置为测试集，并对条件标准偏差进行滚动移动 1 步预测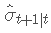， . 我们每 50 次观察重新估计 GARCH 参数。

roll = garhrol(spec = model.spec )#测试集 500 个观察
mean(ret) + rolldesiy\[,'Siga'\]*qdist(dis='std',

回测

让 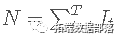 是 T 期间股票收益率低于 VaR 估计值的天数，其中如果 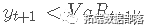 It 为 1，  和 如果  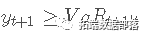， It 为 0 . 因此，N 是样本中观察到的异常数。正如 Kupiec (1995) 所论证的那样，失败数遵循二项式分布 B(T, p)。

for(i in 1:50 p\[i\]= (pbinom(q = (i-1 ) - pbinom(q ))qplot(y = p )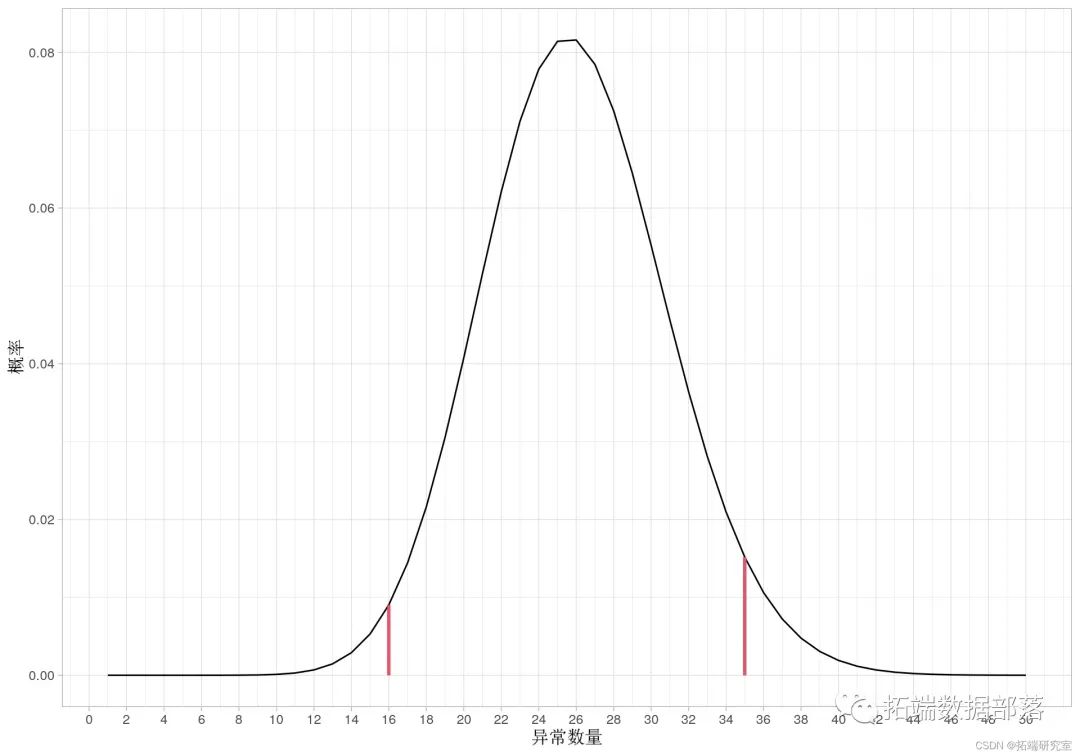

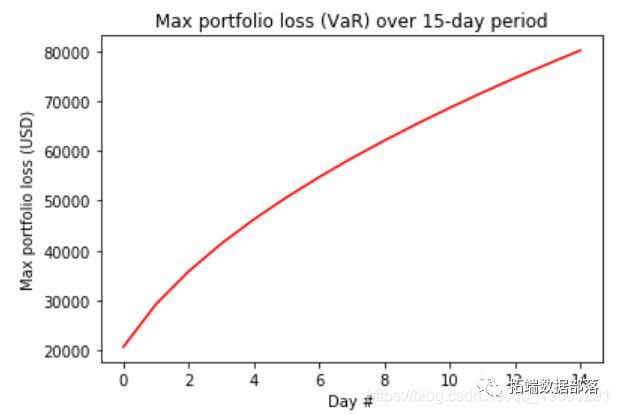
上图表示由二项式分布给出的异常概率分布。预期数量为 25 (=500obs. x 5%)。两条红线表示 95% 的置信水平，较低的是 16  ，较高的是 35。因此，当我们检查测试集上的异常时，我们期望 16 到 35 之间的数字表明 GARCH 模型预测成功。

plot(VaR95, geom = 'line') +geom_point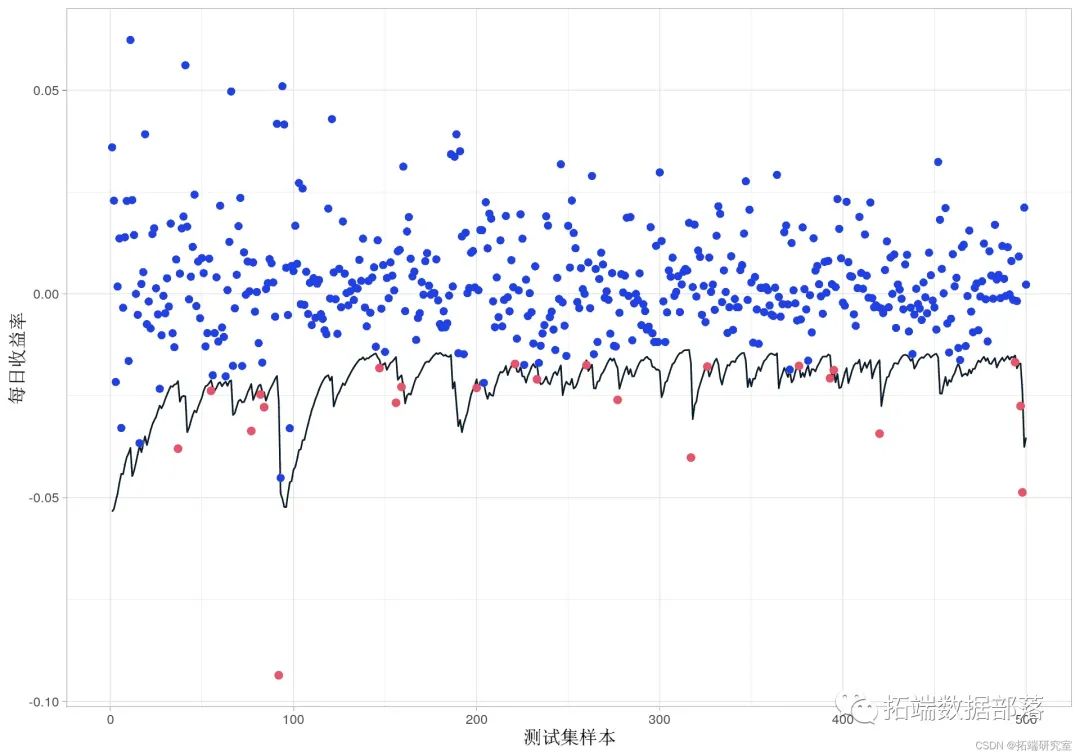

黑线代表 GARCH 模型给出的每日预测 VaR，红点代表低于 VaR 的收益率。最后一步是计算异常的数量，并将其与使用 delta-normal 方法生成的异常进行比较。

cat('delta-normal 方法的异常数：', (sum(rets\[759:1258\] < (mean(r\]

正如我们之前所说，我们预计 delta-normal 方法会高估风险。回测时，只有 14 倍的收益率低于 VaR 低于 95% 显着性水平 (<16)。另一方面，在这种特殊情况下，GARCH 方法（23 个例外）似乎是一种有效的预测工具。

参考

Angelidis T., Benos A. and Degiannakis S. (December 2003). The Use of GARCH Models in VaR Estimation.

---

点击文末“阅读原文”

获取全文完整资料。

本文选自《R语言风险价值：ARIMA，GARCH，Delta-normal法滚动估计VaR（Value at Risk）和回测分析股票数据》。

点击标题查阅往期内容

R语言GARCH模型对股市sp500收益率bootstrap、滚动估计预测VaR、拟合诊断和蒙特卡罗模拟可视化

R语言单变量和多变量（多元）动态条件相关系数DCC-GARCH模型分析股票收益率金融时间序列数据波动率

R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

GARCH-DCC模型和DCC（MVT）建模估计

R语言预测期货波动率的实现：ARCH与HAR-RV与GARCH，ARFIMA模型比较

ARIMA、GARCH 和 VAR模型估计、预测ts 和 xts格式时间序列

PYTHON用GARCH、离散随机波动率模型DSV模拟估计股票收益时间序列与蒙特卡洛可视化

极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR：多元化投资组合预测风险测度分析

Garch波动率预测的区制转移交易策略

金融时间序列模型ARIMA 和GARCH 在股票市场预测应用

时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

R语言风险价值：ARIMA，GARCH，Delta-normal法滚动估计VaR（Value at Risk）和回测分析股票数据

R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化

Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用

MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测

R语言极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR：多元化投资组合预测风险测度分析

Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列

R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列

Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测

R语言时间序列GARCH模型分析股市波动率

R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计

Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测

使用R语言对S＆P500股票指数进行ARIMA + GARCH交易策略

R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模

R语言股票市场指数：ARMA-GARCH模型和对数收益率数据探索性分析

R语言多元Copula GARCH 模型时间序列预测

R语言使用多元AR-GARCH模型衡量市场风险

R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

R语言用Garch模型和回归模型对股票价格分析

GARCH（1,1），MA以及历史模拟法的VaR比较

matlab估计arma garch 条件均值和方差模型