目录

题目：

示例：

分析：

代码：

---

题目：

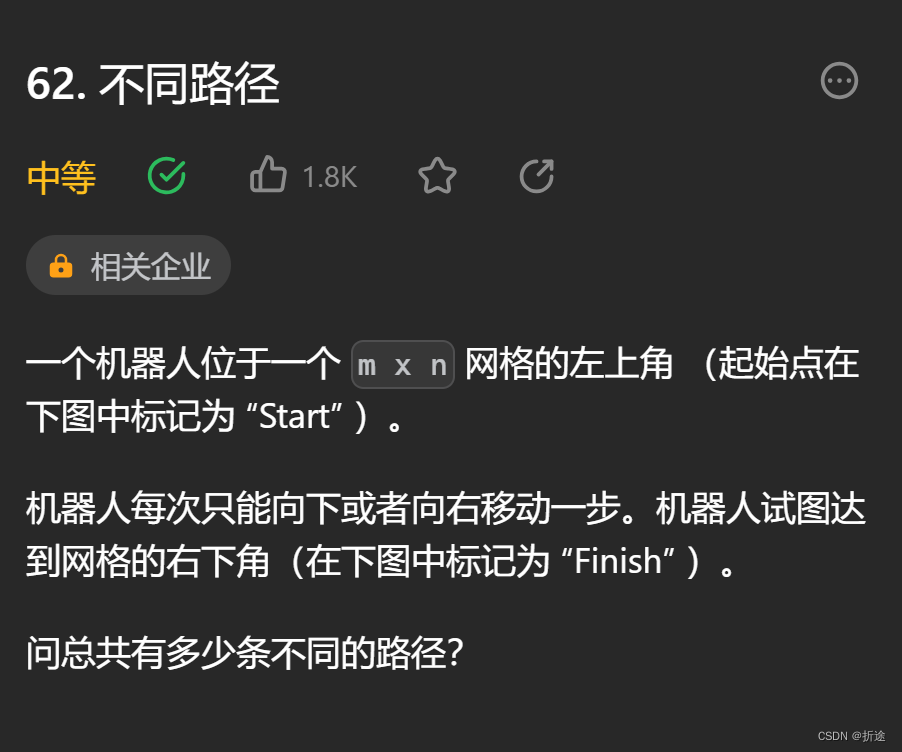
示例：

分析：

题目给我们返回地图的长和宽。问我们从地图的左上走到右下有几种方法。我们只能往下走或是往右走。

这个算是简单的二维动态规划题了。

我们先搞清楚一个问题，我们走到某个格子有几种方法，由于我们只能往下走或是往右走，所以我们只能从上方或是左方走来。所以走到某个格子的方法只有两种，那就是从左走来或是从上走来。

而走到本格的上格的方法也是只有两种，那就是本格的上格的上格以及本格的上格的左格。而走到本格的左格也是一样的。那么我们拿二维的dp数组来存放走到对应地图的方法数。

dp[ i ][ j ]的含义就是我们走到地图的 i 行 j 列有几种方法。

那么我们知道走到某格子只能从上面和左边来，所以dp[ i ][ j ] = dp[ i -1 ][ j ] + dp [ i ][ j - 1 ]

这个意思就是走到某格子的方法数等于走到本格上面的方法数以及走到本格左边的方法数。

那么我们的递推公式是需要行-1，列-1，所以我们用递推公式至少得是行大于等于1以及列大于等于1。所以我们要先把行号为0以及列号为0的dp数组都给初始化。

那么我们知道地图中行号为0的是地图矩阵的最上面的一条边，列号为0的是地图矩阵最左边的一条边。而要走到那两条边的格子，都是只有一种方法，所以我们把dp数组都初始化为1。

递推完毕之后返回dp数组的最后一个元素就好了。

代码：

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>>dp(m,vector<int>(n,1));for(int i=1;i<m;i++){for(int j=1;j<n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];//从上方走过来+从左方走过来.}}return dp[m-1][n-1];}
};