目录

一、实验介绍

 二、实验环境

1. 配置虚拟环境

2. 库版本介绍

三、实验内容

1. 一维卷积

a. 概念

b. 示例

c. 分类

窄卷积（Narrow Convolution）

宽卷积（Wide Convolution）

等宽卷积（Same Convolution）

d. pytorch实现

2. 二维卷积

a. 概念

b. 示例

c. pytorch实现

---

一、实验介绍

        本文主要介绍了卷积运算及其Pytorch实现，包括一维卷积（窄卷积、宽卷积、等宽卷积）、二维卷积。

  

 二、实验环境

    本系列实验使用了PyTorch深度学习框架，相关操作如下：

1. 配置虚拟环境

conda create -n DL python=3.7 

conda activate DL

pip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio==0.8.1 -f https://download.pytorch.org/whl/torch_stable.html

conda install matplotlib

 conda install scikit-learn

2. 库版本介绍

软件包	本实验版本	目前最新版
matplotlib	3.5.3	3.8.0
numpy	1.21.6	1.26.0
python	3.7.16
scikit-learn	0.22.1	1.3.0
torch	1.8.1+cu102	2.0.1
torchaudio	0.8.1	2.0.2
torchvision	0.9.1+cu102	0.15.2

三、实验内容

ChatGPT：

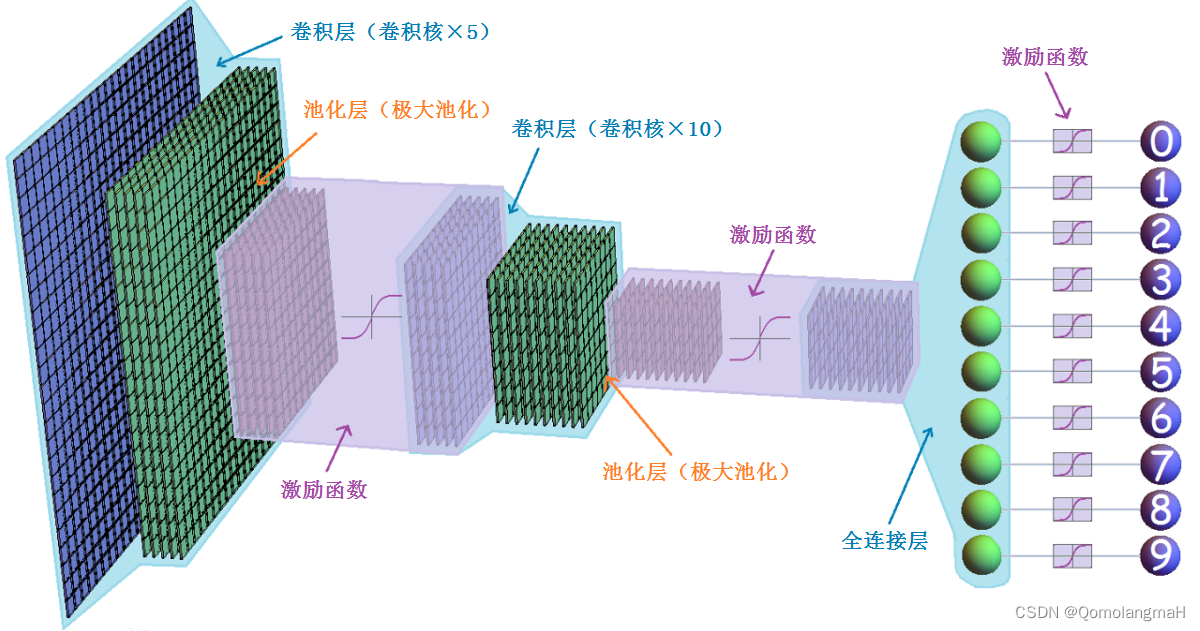
        卷积神经网络（Convolutional Neural Network，简称CNN）是一种深度学习模型，广泛应用于图像识别、计算机视觉和模式识别等领域。它的设计灵感来自于生物学中视觉皮层的工作原理。

        卷积神经网络通过多个卷积层、池化层和全连接层组成。

• 卷积层主要用于提取图像的局部特征，通过卷积操作和激活函数的处理，可以学习到图像的特征表示。
• 池化层则用于降低特征图的维度，减少参数数量，同时保留主要的特征信息。
• 全连接层则用于将提取到的特征映射到不同类别的概率上，进行分类或回归任务。

        卷积神经网络在图像处理方面具有很强的优势，它能够自动学习到具有层次结构的特征表示，并且对平移、缩放和旋转等图像变换具有一定的不变性。这些特点使得卷积神经网络成为图像分类、目标检测、语义分割等任务的首选模型。除了图像处理，卷积神经网络也可以应用于其他领域，如自然语言处理和时间序列分析。通过将文本或时间序列数据转换成二维形式，可以利用卷积神经网络进行相关任务的处理。

1. 一维卷积

a. 概念

        一维卷积是指在一维输入数据上应用滤波器（也称为卷积核或核）的操作。一维卷积在信号处理、自然语言处理等领域中有广泛的应用。

        假设我们有一个长度为n的输入向量和一个长度为m的卷积核。一维卷积的计算过程如下：

• 将卷积核与输入向量的第一个元素对齐，进行元素相乘并求和。这个求和结果将作为卷积操作的输出值的第一个元素。

• 将卷积核向右移动一个位置，再次进行相乘求和的操作。重复这个过程，直到卷积核覆盖完整个输入向量。

  • 输出向量的长度将是 M - K + 1，其中 M 是输入向量的长度，K 是卷积核的长度。

b. 示例

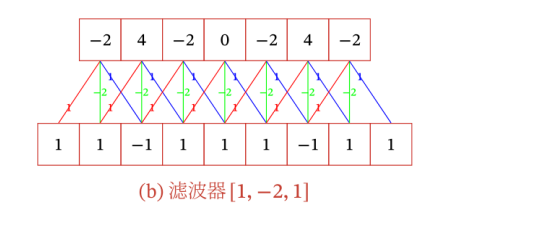
        假设我们有一个输入向量 [1, 1, -1, 1, 1, 1, -1, 1, 1]，和一个卷积核[1, -2, 1]。我们可以按照以下步骤进行一维卷积（窄卷积）计算：

• 第一个元素的计算：(1 * 1) + (1 * -2) + (-1 * 1) = -2
• 第二个元素的计算：(1 * 1) + (-1 * -2) + (1 * 1) = 4
• 第三个元素的计算：(-1 * 1) + (1 * -2) + (1 * 1) = -2
• ………………

c. 分类

卷积的结果按输出长度不同可以分为三类：

• 窄卷积（Narrow Convolution）

  • 步长 𝑇 = 1，两端不补零 𝑃 = 0
  • 卷积后输出长度为 𝑀 − 𝐾 +1

• 宽卷积（Wide Convolution）

  • 步长 𝑇 = 1，两端不补零 𝑃 = 𝐾 -1
  • 卷积后输出长度为 𝑀 + 𝐾 - 1

• 等宽卷积（Same Convolution）

  • 步长 𝑇 = 1，两端不补零 𝑃 = (𝐾 -1) / 2
  • 卷积后输出长度为 𝑀

注意：

• 在早期的文献中，卷积一般默认为窄卷积；
• 而目前的文献中，卷积一般默认为等宽卷积。

d. pytorch实现

import torch
import torch.nn.functional as F# 转换输入特征图和滤波器为张量
input_tensor = torch.tensor([1, 1, -1, 1, 1, 1, -1, 1, 1], dtype=torch.float32)
filter_tensor = torch.tensor([1, -2, 1], dtype=torch.float32)# 窄卷积计算
narrow_conv = F.conv1d(input_tensor.view(1, 1, -1), filter_tensor.view(1, 1, -1), stride=1, padding=0)
print("Narrow Convolution Result:")
print(narrow_conv)# 宽卷积计算
wide_conv = F.conv1d(input_tensor.view(1, 1, -1), filter_tensor.view(1, 1, -1), stride=1, padding=2)
print("Wide Convolution Result:")
print(wide_conv)# 等宽卷积计算
same_width_conv = F.conv1d(input_tensor.view(1, 1, -1), filter_tensor.view(1, 1, -1), stride=1, padding=1)
print("Same Width Convolution Result:")
print(same_width_conv)

输出：

 

2. 二维卷积

a. 概念

        二维卷积是一种常用的图像处理操作，它可以应用于二维图像或矩阵数据上。在二维卷积中，我们使用一个称为滤波器或卷积核的小矩阵对输入数据进行扫描和计算。在每个位置上，滤波器与输入数据的对应元素进行逐元素相乘，然后将所有乘积相加，得到输出的一个元素。通过滑动滤波器，我们可以在输入数据上执行卷积操作，并生成输出特征图。

        具体而言，对于一个二维卷积操作，我们需要指定以下参数：

• 输入数据：一个二维的输入矩阵或图像，通常表示为一个矩阵，其中每个元素代表一个像素值或特征值。
• 滤波器（卷积核）：一个小的二维矩阵，用于扫描输入数据并执行卷积操作。滤波器的大小通常是正方形，例如3x3、5x5等。
• 步幅（stride）：指定滤波器在输入数据上滑动的步长。例如，如果步幅为1，则滤波器每次滑动一个元素；如果步幅为2，则滤波器每次滑动两个元素。
• 边界处理方式：决定如何处理输入数据边界上的情况。常见的方式包括补零（zero-padding）和截断（truncate）。

b. 示例

        假设有一个输入特征图（input feature map）的大小为5x5，其中的元素值如下所示：

[[1, 1, 1, 1, 1],[-1, 0, -3, 0, 1],[2, 1, 1, -1, 0],[0, -1, 1, 2, 1],[1, 2, 1, 1, 1]]

        现在我们有一个大小为3x3的卷积核（filter）如下所示：

[[1, 0, 0],[0, 0, 0],[0, 0, -1]]

        我们可以通过滑动窗口的方式将卷积核在输入特征图上进行计算。假设滑动步长（stride）为1，即每次滑动一个像素进行计算。以计算特征图第三个元素为例，计算过程如下：

• 输入矩阵的子矩阵：

 1 1 1 
-1 0 -3 2 1 1 

• 将卷积核的左上角放在输入特征图的第三个元素处，进行逐元素相乘并求和：

(1 * 1) + (1 * 0) + (1 * 0) + 
(-1 * 0) + (0 * 0) + (-3 * 0) + 
(2 * 0) + (1 * 0) + (1 * -1) = 1

将计算结果1作为特征图的第三个元素。

c. pytorch实现

import torch
import torch.nn as nn# 创建输入张量
input_tensor = torch.tensor([[1, 1, 1, 1, 1],[-1, 0, -3, 0, 1],[2, 1, 1, -1, 0],[0, -1, 1, 2, 1],[1, 2, 1, 1, 1]], dtype=torch.float32).unsqueeze(0).unsqueeze(0)# 创建卷积核张量
kernel_tensor = torch.tensor([[1, 0, 0],[0, 0, 0],[0, 0, -1]], dtype=torch.float32).unsqueeze(0).unsqueeze(0)# 翻转卷积核张量
kernel_tensor_flipped = torch.flip(kernel_tensor, [2, 3])# 定义卷积层
conv_layer = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, bias=False)# 将翻转后的卷积核张量加载到卷积层的权重中
conv_layer.weight.data = kernel_tensor_flipped# 执行卷积运算
output_tensor = conv_layer(input_tensor)# 打印输出张量
print(output_tensor)

• 创建一个输入张量input_tensor和一个卷积核张量kernel_tensor
  • input_tensor是一个5x5的浮点型张量，表示上文所示输入数据。
  • kernel_tensor是一个3x3的浮点型张量，表示上文所示卷积核。
• 使用torch.flip函数对卷积核张量进行翻转操作。（这个操作是为了将卷积核应用于输入数据时实现卷积运算的正确性）
• 使用nn.Conv2d类定义了一个卷积层conv_layer。
  • in_channels参数指定了输入张量的通道数，这里为1；
  • out_channels参数指定了输出张量的通道数，这里也为1；
  • kernel_size参数指定了卷积核的尺寸，这里为3；
  • bias参数指定是否使用偏置项，这里为False。
• 将翻转后的卷积核张量加载到卷积层的权重中，即将kernel_tensor_flipped赋值给conv_layer.weight.data。这样设置了卷积层的权重，使其进行卷积运算时使用了翻转后的卷积核。
• 执行卷积运算，将输入张量input_tensor通过卷积层conv_layer进行卷积操作，得到输出张量output_tensor。

输出：