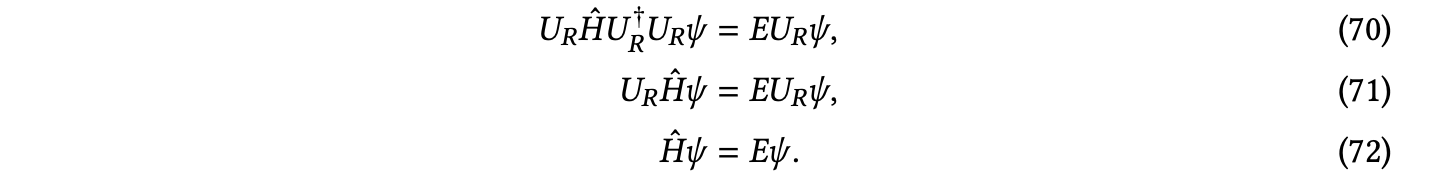课程地址和说明
线性代数p1
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
线性代数
标量
标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,而没有方向,部分有正负之分。物理学中,标量(或作纯量)指在坐标变换下保持不变的物理量。用通俗的说法,标量是只有大小,没有方向的量。(在深度学习领域也是如此)
标量的运算规律
加减法: c = a + b c=a+b c=a+b
乘除法: c = a ⋅ b c=a\cdot b c=a⋅b
取特定函数: c = s i n a c=sina c=sina
长度: ∣ a ∣ = { a , a > 0 − a , a ≤ 0 |a|=\begin{cases} a,a>0\\ -a,a\le 0 \end{cases} ∣a∣={a,a>0−a,a≤0
不等式:
- ∣ a + b ∣ ≤ ∣ a ∣ + ∣ b ∣ |a+b|\le |a|+|b| ∣a+b∣≤∣a∣+∣b∣
- ∣ a ⋅ b ∣ ≤ ∣ a ∣ ⋅ ∣ b ∣ |a\cdot b|\le |a|\cdot|b| ∣a⋅b∣≤∣a∣⋅∣b∣
数域
数域:复数集的一个子集 K K K如果满足:
- 0 , 1 ∈ K 0,1\in K 0,1∈K
- a , b ∈ K ⟹ a ± b , a b ∈ K a,b\in K\Longrightarrow a\pm b,ab\in K a,b∈K⟹a±b,ab∈K
- a , b ∈ K , 且 b ≠ 0 ⟹ a b ∈ K a,b\in K,且b\ne 0\Longrightarrow \frac{a}{b}\in K a,b∈K,且b=0⟹ba∈K
那么称 K K K是一个数域
【注】定义的第一条是说明0和1都在集合 K K K中,第二条是说明当 a , b a,b a,b都在集合 K K K中,则 a ± b a\pm b a±b与 a b ab ab的结果也在集合 K K K中,第三条是说明当 a , b a,b a,b都在集合 K K K中,则 a b , b ≠ 0 \frac{a}{b},b\ne 0 ba,b=0也在集合 K K K中,用这种方法我们可以定义有理数域,因为0,1在集合中,然后四则运算也在集合中,仅靠多次累加累乘等操作就能定义有理数。
【问】为什么定义数域?
【转自知乎,原贴地址:为什么要定义数域呢?】
定义数域的原因在于数学家希望建立一个具有良好性质和规律的数学结构,以方便进行计算和理论研究。数域是代数结构中的一个基本概念,它包含了一组满足特定运算法则的数。研究数域可以帮助我们更好地理解数学对象之间的关系,例如实数、有理数、整数等。
封闭性是数域的一个重要特性。在数域中,对于给定的运算(如加法、减法、乘法和除法等),结果仍然属于同一个数域。保证封闭性有几个好处:
- 简化计算:在一个封闭的数域中,我们可以对数进行各种运算,而不必担心结果会跳出这个域。这大大简化了计算过程,使我们能够更方便地处理数学问题。
- 方程的解有意义:当我们在研究方程时,封闭性确保了我们在求解过程中得到的解依然属于原始数域。这使得解更具有意义,因为我们可以在同一个数学框架内讨论和研究这些解。
- 易于理解和操作:保证封闭性有助于我们更好地理解数学概念,因为我们可以在一个统一的框架内讨论和操作数学对象。这也为研究数学性质提供了便利,因为我们可以在一个封闭的环境中探讨不同数学对象之间的关系。
- 探索新的数学结构:研究封闭性有助于数学家发现新的数学结构,从而推动数学领域的发展。例如,复数的引入解决了一些实数域中无法解决的方程,从而使我们的数学体系更加完善。
总之,保证封闭性有助于我们在数学领域中建立统一的框架,简化计算过程,并使方程的解具有意义。封闭性还有助于我们更好地理解和操作数学概念,以及发现新的数学结构。
由于我不是学数学的,下面这些我不证明,都当作结论用:
- 有理数集 Q \textbf{Q} Q,实数集 R \textbf{R} R,复数集 C \textbf{C} C都是数域;但是整数集 Z \textbf{Z} Z不是数域,因为 Z \textbf{Z} Z对于除法不封闭(整数与整数做除法,如果不能整除,将产生小数,产生的小数又分为有限小数和无限不循环小数,有限小数是有理数,无限不循环小数是无理数,所以整数除整数得到的可能是整数、有理数或无理数,整数除整数不一定就是整数,所以整数集对除法不封闭)
【注】封闭性,即闭包 (数学)。数学中,若对某个集合的成员进行一种运算,生成的仍然是这个集合的成员,则该集合被称为在这个运算下闭合。
- 任一数域都包含有理数域,即有理数域是最小的数域
n n n维向量空间 K n K^{n} Kn
这里可能我理解的有问题,我参考的是丘维声老师的高等代数教材加上我自己的理解,如果有数学专业的大佬发现我理解的有问题请指正。
- 有序对:在数学中,有序偶是两个对象的搜集,使得可以区分出其中一个是“第一个元素”而另一个是“第二个元素”(第一个元素和第二个元素也叫做左投影和右投影)。带有第一个元素 a a a和第二个元素 b b b的有序偶通常写为 ( a , b ) (a,b) (a,b)
- n n n元有序组: n n n元有序组(ordered n-tuples)亦称 n n n目有序组,是有序对的推广,按一定顺序给出的 n ( n ≥ 1 ) n(n≥1) n(n≥1)个客体称为一个n元有序组。依次给出 n n n个客体(这个客体可以是任意的东西) x 1 , x 2 , … , x n x_{1},x_{2},…,x_{n} x1,x2,…,xn得到的n元有序组记为 〈 x 1 , x 2 , … , x n 〉 〈x_{1},x_{2},…,x_{n}〉 〈x1,x2,…,xn〉(或 ( x 1 , x 2 , … , x n (x_{1},x_{2},…,x_{n} (x1,x2,…,xn),其中 x i x_{i} xi常称为有序组的第 i i i分量,元数不同的两个有序组不等,两个 n n n元有序组 〈 x 1 , x 2 , … , x n 〉 〈x_{1},x_{2},…,x_{n}〉 〈x1,x2,…,xn〉与 〈 y 1 , y 2 , … , y n 〉 〈y_{1},y_{2},…,y_{n}〉 〈y1,y2,…,yn〉相等,当且仅当对每一个 i ∈ { 1 , 2 , … , n } i\in\left \{1,2,…,n\right \} i∈{1,2,…,n},有 x i = y i x_{i}=y_{i} xi=yi.【比如:表示日期:年、月、日可用三元有序组表示:(年, 月, 日)。】
- n n n元有序数组:将 n n n元有序组中的分量都定义为数字就是 n n n元有序数组(我个人理解,不严谨,欢迎数学大佬给出严谨的定义)
- n n n元有序数组组成的集合:取定一个数域 K K K,设 n n n是任意给定的一个正整数,令 K n = { ( a 1 , a 2 , . . . , a n ) ∣ a i ∈ K , i = 1 , 2 , . . . , n } K^{n}=\left \{(a_{1},a_{2},...,a_{n})|a_{i}\in K,i=1,2,...,n\right \} Kn={(a1,a2,...,an)∣ai∈K,i=1,2,...,n},则称 K n K^{n} Kn是 n n n元有序数组组成的集合。
- 相等关系:在 K n K^{n} Kn中,如果 a 1 = b 1 , a 2 = b 2 , . . . , a n = b n a_{1}=b_{1},a_{2}=b_{2},...,a_{n}=b_{n} a1=b1,a2=b2,...,an=bn,则称 K n K^{n} Kn中的两个元素(有序数组) ( a 1 , a 2 , . . . , a n ) (a_{1},a_{2},...,a_{n}) (a1,a2,...,an)与 ( b 1 , b 2 , . . . , b n ) (b_{1},b_{2},...,b_{n}) (b1,b2,...,bn)相等。
- 加法运算:在 K n K^{n} Kn中,规定加法运算如下, ( a 1 , a 2 , . . . , a 3 ) + ( b 1 , b 2 , . . . , b 3 ) = ( a 1 + b 1 , a 2 + b 2 , . . . , a n + b n ) (a_{1},a_{2},...,a_{3})+(b_{1},b_{2},...,b_{3})=(a_{1}+b_{1},a_{2}+b_{2},...,a_{n}+b_{n}) (a1,a2,...,a3)+(b1,b2,...,b3)=(a1+b1,a2+b2,...,an+bn)
- 数量乘法: k ( a 1 , a 2 , . . . , a n ) = ( k a 1 , k a 2 , . . . , k a n ) k(a_{1},a_{2},...,a_{n})=(ka_{1},ka_{2},...,ka_{n}) k(a1,a2,...,an)=(ka1,ka2,...,kan)
- 在 K n K^{n} Kn中规定加法和数量乘法满足8条法则,其中, α , β , γ ∈ K n , k , l ∈ K \alpha,\beta,\gamma\in K^{n},k,l\in K α,β,γ∈Kn,k,l∈K:
- 加法交换律: α + β = β + α \bm{\alpha}+\bm{\beta}=\bm{\beta}+\bm{\alpha} α+β=β+α
- 加法结合律: ( α + β ) + γ = α + ( β + γ ) (\bm{\alpha}+\bm{\beta})+\bm{\gamma}=\bm{\alpha}+(\bm{\beta}+\bm{\gamma}) (α+β)+γ=α+(β+γ)
- 零元:把 ( 0 , 0 , . . . , 0 ) (0,0,...,0) (0,0,...,0)记作 0 \bm{0} 0,它使得 0 + α = α + 0 \bm{0}+\bm{\alpha}=\bm{\alpha}+\bm{0} 0+α=α+0,称 0 \bm{0} 0是 K n K^{n} Kn的零元。
- 负元:对于 α = ( a 1 , a 2 , . . . , a n ) ∈ K n \bm{\alpha}=(a_{1},a_{2},...,a_{n})\in K^{n} α=(a1,a2,...,an)∈Kn,令 − α = ( − a 1 , − a 2 , . . . , − a n ) ∈ K n -\bm{\alpha}=(-a_{1},-a_{2},...,-a_{n})\in K^{n} −α=(−a1,−a2,...,−an)∈Kn,有 α + ( − α ) = ( − α ) + α = 0 \bm{\alpha}+(-\bm{\alpha})=(-\bm{\alpha})+\bm{\alpha}=\bm{0} α+(−α)=(−α)+α=0,则称 − α -\bm{\alpha} −α是 α \bm{\alpha} α的负元
- 1 α = α 1\bm{\alpha}=\bm{\alpha} 1α=α
- ( k l ) α = k ( l α ) (kl)\bm{\alpha}=k(l\bm{\alpha}) (kl)α=k(lα)
- ( k + l ) α = k α + l α (k+l)\bm{\alpha}=k\bm{\alpha}+l\bm{\alpha} (k+l)α=kα+lα
- k ( α + β ) = k α + k β k(\bm{\alpha}+\bm{\beta})=k\bm{\alpha}+k\bm{\beta} k(α+β)=kα+kβ
向量
在数学中,向量(也称为欧几里得向量、几何向量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。下面给出相关概念的精确定义。
向量空间
数域 K K K上所有 n n n元有序数组组成的集合 K n K^{n} Kn,连同定义在它上面的加法运算和数量乘法运算,及其满足的8条运算法则一起,称为数域 K K K上的一个 n n n维度向量空间。
向量的定义
K n K^{n} Kn的元素称为 n n n维向量,记为 α = ( a 1 , a 2 , . . . , a n ) \bm{\alpha}=(a_{1},a_{2},...,a_{n}) α=(a1,a2,...,an),称 a i a_{i} ai是 α \bm{\alpha} α的第 i i i个分量,其在欧几里得空间下用一个有方向的箭头表示,在数学上一般用粗体或者字母上面带箭头表示向量。假设有向量 α = ( a 1 , a 2 , . . . , a n ) \bm{\alpha}=(a_{1},a_{2},...,a_{n}) α=(a1,a2,...,an)与向量 β = ( b 1 , b 2 , . . . , b n ) \bm{\beta}=(b_{1},b_{2},...,b_{n}) β=(b1,b2,...,bn)(以下均章节均按此假定)
- n n n元有序数组写成一行 ( a 1 , a 2 , . . . , a n ) (a_{1},a_{2},...,a_{n}) (a1,a2,...,an),称为行向量,写成一列 ( a 1 a 2 ⋮ a n ) \begin{pmatrix} a_{1}\\ a_{2} \\ \vdots \\ a_{n} \end{pmatrix} a1a2⋮an ,称为列向量。
- 行列向量通过取转置符号 T T T进行变换,比如行向量 α = ( a 1 , a 2 , . . . , a n ) \bm{\alpha}=(a_{1},a_{2},...,a_{n}) α=(a1,a2,...,an)的转置向量就是列向量 α T = ( a 1 a 2 ⋮ a n ) \bm{\alpha}^{T}=\begin{pmatrix} a_{1}\\ a_{2} \\ \vdots \\ a_{n} \end{pmatrix} αT= a1a2⋮an
- 向量与向量转置的乘法为: α β T = ( a 1 , a 2 , . . . , a n ) ( b 1 b 2 ⋮ b n ) = a 1 b 1 + a 2 b 2 + . . . + a n b n \bm{\alpha}\bm{\beta}^{T}=(a_{1},a_{2},...,a_{n})\begin{pmatrix} b_{1}\\ b_{2} \\ \vdots \\ b_{n} \end{pmatrix}=a_{1}b_{1}+a_{2}b_{2}+...+a_{n}b_{n} αβT=(a1,a2,...,an) b1b2⋮bn =a1b1+a2b2+...+anbn
向量的运算规律
向量完全符合上述数域 K K K上所有 n n n元有序数组组成的集合 K n K^{n} Kn,连同定义在它上面的加法运算和数量乘法运算,及其满足的8条运算法则。以下给出向量在深度学习中的常见运算规律:
【符号说明】假设向量为 x \textbf{x} x,则其中的元素为 x i , i = 1 , 2 , 3... x_{i},i=1,2,3... xi,i=1,2,3...
-
加减法: c = a + b \textbf{c}=\textbf{a}+\textbf{b} c=a+b,其中 c i = a i + b i c_{i}=a_{i}+b_{i} ci=ai+bi

-
数乘: c = α ⋅ b \textbf{c}=\alpha\cdot \textbf{b} c=α⋅b,其中 c i = α ⋅ b i c_{i}=\alpha\cdot b_{i} ci=α⋅bi, α \alpha α是一个常数

-
取函数: c = s i n a \textbf{c}=sin\textbf{a} c=sina,其中 c i = s i n a i c_{i}=sina_{i} ci=sinai
向量的长度(模长)
向量 α \bm{\alpha} α的长度(模长) ∣ ∣ α ∣ ∣ ||\bm{\alpha}|| ∣∣α∣∣为:
∣ ∣ α ∣ ∣ = ∑ i = 1 n a i 2 = a 1 2 + a 2 2 + . . . + a n 2 ≥ 0 ||\bm{\alpha}||=\sqrt{\sum\limits_{i=1}^{n} a_{i}^{2}}=\sqrt{a_{1}^{2}+a_{2}^{2}+...+a_{n}^{2}}\ge 0 ∣∣α∣∣=i=1∑nai2=a12+a22+...+an2≥0
其中:
- ∣ ∣ α ∣ ∣ ≥ 0 ||\bm{\alpha}||\ge 0 ∣∣α∣∣≥0
- ∣ ∣ α + β ∣ ∣ ≤ ∣ ∣ α ∣ ∣ + ∣ ∣ β ∣ ∣ ||\bm{\alpha}+\bm{\beta}||\le ||\bm{\alpha}||+||\bm{\beta}|| ∣∣α+β∣∣≤∣∣α∣∣+∣∣β∣∣
- ∣ ∣ α ⋅ β ∣ ∣ = ∣ ∣ α ∣ ∣ ⋅ ∣ ∣ β ∣ ∣ ||\bm{\alpha}\cdot \bm{\beta}||=||\bm{\alpha}||\cdot ||\bm{\beta}|| ∣∣α⋅β∣∣=∣∣α∣∣⋅∣∣β∣∣
向量的叉乘(外积)
向量的叉乘(外积),也叫向量积。结果是一个和已有两个向量都垂直的向量(法向量)。
- 在平面中,向量的叉乘的模长为 ∣ ∣ α × β ∣ ∣ = ∣ ∣ α ∣ ∣ ∙ ∣ ∣ β ∣ ∣ ∙ s i n θ ||\bm{\alpha}\times \bm{\beta}||=||\bm{\alpha}||\bullet ||\bm{\beta}||\bullet sin\theta ∣∣α×β∣∣=∣∣α∣∣∙∣∣β∣∣∙sinθ,其中 s i n θ sin\theta sinθ是向量 α \bm{\alpha} α与向量 β \bm{\beta} β的夹角的正弦值
- 在三维空间中(假设 n = 3 n=3 n=3),向量的叉乘是指一个与这两个向量都垂直的向量,即:
α × β = ∣ i j k a 1 a 2 a 3 b 1 b 2 b 3 ∣ \bm{\alpha}\times \bm{\beta}=\begin{vmatrix} i& j& k\\ a_{1}&a_{2} &a_{3} \\ b_{1}& b_{2} &b_{3} \end{vmatrix} α×β= ia1b1ja2b2ka3b3
【注】这是一个行列式,行列式的计算方法参考:第一章----行列式知识点汇总
向量的点乘(内积)
向量 α \bm{\alpha} α与向量 β \bm{\beta} β的点乘结果为:
α ⋅ β = α β T = a 1 b 1 + a 2 b 2 + . . . + a n b n \bm{\alpha}\cdot \bm{\beta}=\bm{\alpha} \bm{\beta}^{T}=a_{1}b_{1}+a_{2}b_{2}+...+a_{n}b_{n} α⋅β=αβT=a1b1+a2b2+...+anbn
向量正交
两个向量正交说明两个向量相互垂直,即下图:

当两个向量的点乘结果为0时,两个向量正交,即当 α ⋅ β = α β T = a 1 b 1 + a 2 b 2 + . . . + a n b n = 0 \bm{\alpha}\cdot \bm{\beta}=\bm{\alpha} \bm{\beta}^{T}=a_{1}b_{1}+a_{2}b_{2}+...+a_{n}b_{n}=0 α⋅β=αβT=a1b1+a2b2+...+anbn=0时,向量 α \bm{\alpha} α与向量 β \bm{\beta} β正交。
矩阵
矩阵的定义
- 由 s ⋅ m s\cdot m s⋅m个数排成 s s s行、 m m m列的一张表称为一个 s × m s\times m s×m矩阵,其中的每一个数称为这个矩阵的一个元素,第 i i i行与第 j j j列交叉位置的元素称为矩阵 ( i , j ) (i,j) (i,j)元。
- 矩阵通常用大写英文字母 A , B , C , . . . \bm{A},\bm{B},\bm{C},... A,B,C,...表示,一个 s × m s\times m s×m矩阵可以简记为 A s × m \bm{A}_{s\times m} As×m,它的 ( i , j ) (i,j) (i,j)元记作 A ( i ; j ) \bm{A}(i;j) A(i;j)。如果矩阵 A \bm{A} A的 ( i , j ) (i,j) (i,j)元是 a i j a_{ij} aij,那么可以记作 A = ( a i j ) \bm{A}=(a_{ij}) A=(aij)
- 元素全为0的矩阵称为零矩阵,简记为 0 \bm{0} 0。 s s s行 m m m列的零矩阵可以记成 0 s × m \bm{0}_{s\times m} 0s×m
- 如果一个矩阵 A \bm{A} A的行数与列数相等,则称它为方阵, m m m行 m m m列的方阵也称为 m m m级矩阵或 m m m阶方阵。
- 对于两个矩阵 A \bm{A} A与 B \bm{B} B,如果它们的行数相等,列数相等,并且 A ( i ; j ) = B ( i ; j ) , i = 1 , 2 , 3... , j = 1 , 2 , 3 , . . . \bm{A}(i;j)=\bm{B}(i;j),i=1,2,3...,j=1,2,3,... A(i;j)=B(i;j),i=1,2,3...,j=1,2,3,...,那么称矩阵 A \bm{A} A与 B \bm{B} B相等,记作 A = B \bm{A}=\bm{B} A=B
- 举一个三阶矩阵的例子:
A = ( 1 1 1 1 1 1 1 1 1 ) \bm{A}=\begin{pmatrix} 1& 1 &1 \\ 1& 1&1 \\ 1 &1 &1 \end{pmatrix} A= 111111111
矩阵的运算规律
假设有矩阵 A B , C \bm{A}\bm{B},\bm{C} AB,C
加法
C = A + B \bm{C}=\bm{A}+\bm{B} C=A+B,其中, c i j = a i j + b i j c_{ij}=a_{ij}+b_{ij} cij=aij+bij,即对应元素相加
数乘
C = α ⋅ B \bm{C}=\alpha\cdot \bm{B} C=α⋅B,其中, c i j = α b i j c_{ij}=\alpha b_{ij} cij=αbij,即对应元素乘相应的常数
取函数
C = s i n A \bm{C}=sin\bm{A} C=sinA,其中 c i j = s i n ( a i j ) c_{ij}=sin(a_{ij}) cij=sin(aij),对应元素取函数
矩阵与向量的乘法
据说是一种空间扭曲,可惜考研数学没接触,以后慢慢看高等代数、解析几何把这里补上




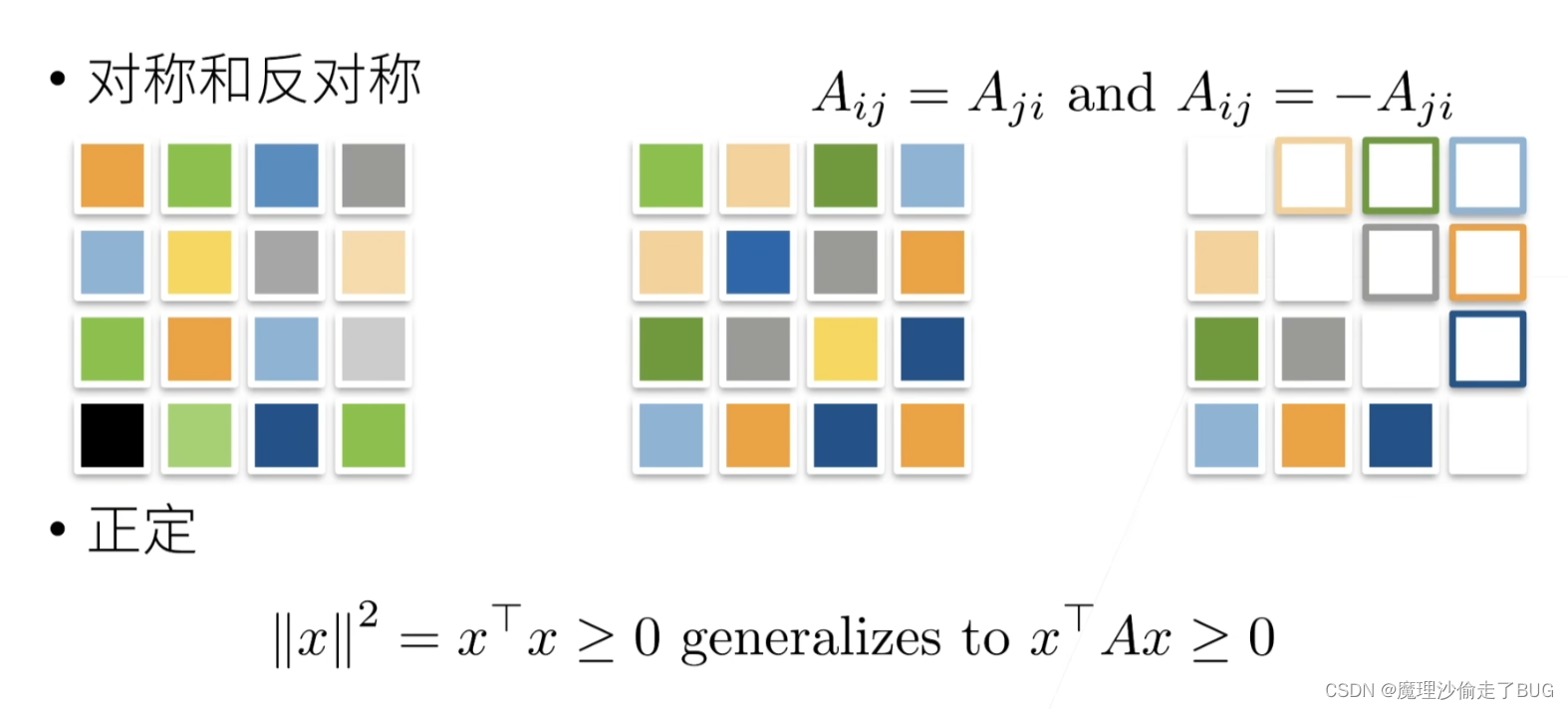

【注】正交矩阵的所有的行向量都是相互正交的,并且正交矩阵和其转置矩阵的乘积是一个对角线为1的单位矩阵,即 U U T = U E \mathbf{U}\mathbf{U^{T}}=\mathbf{U^{E}} UUT=UE