Denoising diffusion probabilistic models (DDPMs)从马尔科夫链中采样生成样本,需要迭代多次,速度较慢。Denoising diffusion implicit models (DDIMs)的提出是为了加速采样过程,减少迭代的次数,并且要求DDIM可以复用DDPM训练的网络。
加速采样的基本思路是,DDPM的生成过程需要从 [ T , ⋯ , 1 ] [T,\cdots,1] [T,⋯,1]的序列逐步采样,DDIM则可以从 [ T , ⋯ , 1 ] [T,\cdots,1] [T,⋯,1]的子序列采样来生成,通过跳步的方式减少采样的步数。
非马尔科夫的前向过程
DDPM中推理分布(inference distribution) q ( x 1 : T ∣ x 0 ) q(\mathbf x_{1:T}|\mathbf x_0) q(x1:T∣x0)是固定的马尔科夫链。DDIM的作者考虑构造新的推理分布,该推理过程和DDPM优化相同的目标,但能产生新的生成过程。

考虑一个推理分布族Q,由实向量 σ ∈ R ≥ 0 T \sigma \in \mathbb{R}^T_{\ge 0} σ∈R≥0T索引:
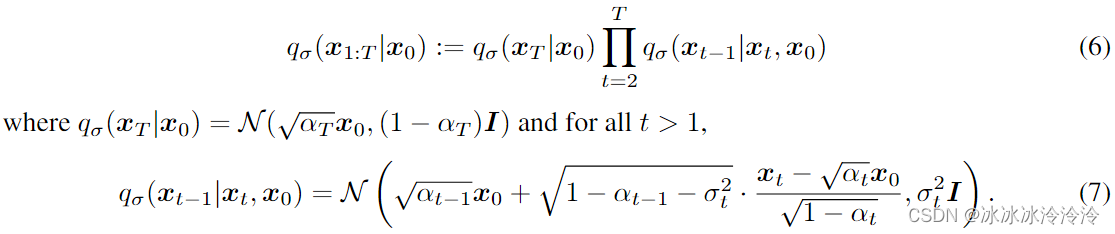
根据上面的定义有 q σ ( x t ∣ x 0 ) = N ( α t x 0 , ( 1 − α t ) I ) q_{\sigma}(\mathbf x_t | \mathbf x_0) = \mathcal{N}(\sqrt{\alpha_t}\mathbf x_0, (1-\alpha_t)I) qσ(xt∣x0)=N(αtx0,(1−αt)I)。
对应的前向过程也是高斯分布:
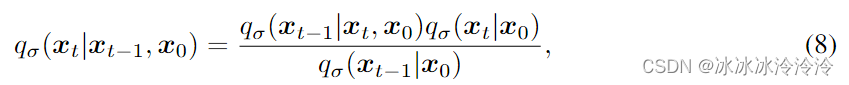
通过上面定义的推理过程,前向过程变成了非马尔科夫的,因为每一步都依赖 x 0 \mathbf x_0 x0。
参数 σ \sigma σ控制前向过程的随机性,如果 σ → 0 \sigma \rightarrow 0 σ→0,那么在已知 x 0 \mathbf x_0 x0和其中任一个 x t \mathbf x_t xt的情况下, x t − 1 \mathbf x_{t-1} xt−1是固定的。
根据上面的推理过程,定义需要学习的生成过程为:
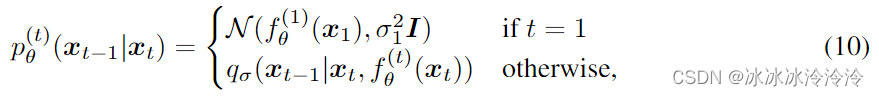
其中
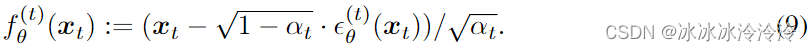
根据上面的定义的推理过程和生成过程,优化的目标是
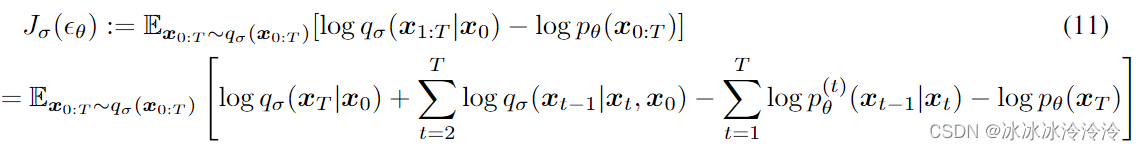
可以证明该优化目标和特定情况下DDPM的优化目标相同。
逆向生成过程的采样方法如下:
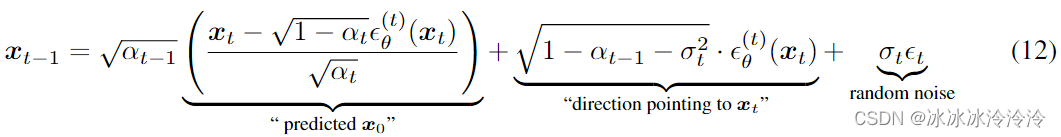
选择不同的 σ \sigma σ值会导致不同的生成过程,但它们使用相同的 ϵ θ \epsilon_{\theta} ϵθ模型。
如果 σ t = ( 1 − α t − 1 ) / ( 1 − α t ) ( 1 − α t ) / ( 1 − α t − 1 ) \sigma_t=\sqrt{(1-\alpha_{t-1})/(1-\alpha_{t})}\sqrt{(1-\alpha_{t})/(1-\alpha_{t-1})} σt=(1−αt−1)/(1−αt)(1−αt)/(1−αt−1),那么前向过程又变成了马尔科夫的,生成过程和DDPM一样。
如果 σ t = 0 \sigma_t=0 σt=0,那么随机噪声前的系数是0, x 0 \mathbf x_0 x0和 x T \mathbf x_T xT之间的关系是固定的,这属于隐概率模型(implicit probabilistic model)。因此,作者把这种情况称为denoising diffusion implicit model (DDIM)。
加速
为了加速采样,作者考虑下面的推理过程:
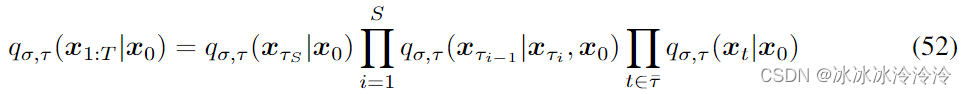
其中 τ \tau τ是长度为S的 [ 1 , ⋯ , T ] [1,\cdots,T] [1,⋯,T]的子序列, τ S = T \tau_S=T τS=T, τ ‾ : = { 1 , … , T } \ τ \overline{\tau}:=\{1,\ldots,T \} \backslash \tau τ:={1,…,T}\τ是除去子序列剩下的序号。
定义
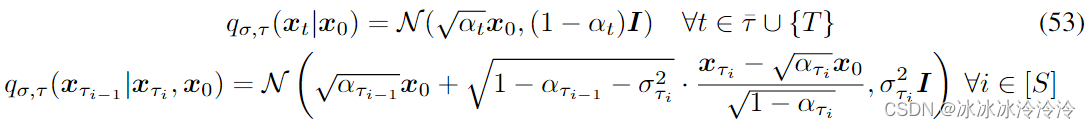 该推理分布对应的生成过程如下:
该推理分布对应的生成过程如下:
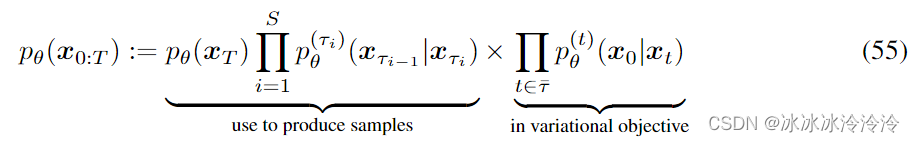
定义需要学习的概率为:
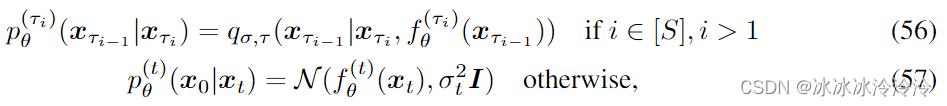
根据上面的定义的推理过程和生成过程,优化的目标是
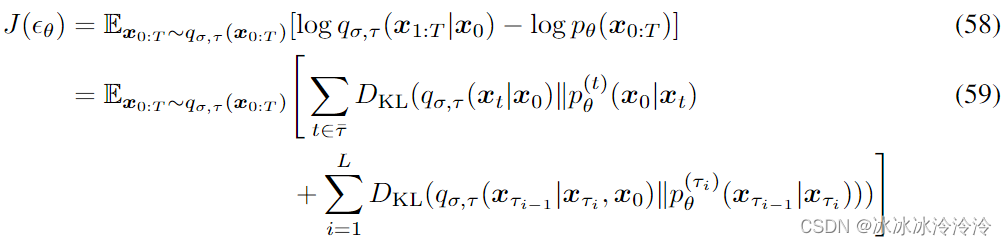
可以证明该优化目标和特定情况下DDPM的优化目标相同。
因此,可以利用DDPM训练的网络,但是从子序列采样生成图像。