7 AI在材料科学中的应用
在这一部分,我们将讨论AI技术在材料科学中的应用。首先,我们将介绍晶体材料的概述,并详细定义晶体材料的物理对称性,具体在第7.1节中讨论。接下来,我们将在第7.2节和第7.3节中讨论两个常见且基础的任务,即材料表示学习问题和材料生成问题。此外,我们还包括了三个高级主题,包括有序晶体材料表征(第7.4节)、无序晶体材料表征(第7.5节)以及声子计算(第7.6节)。
7.1 概述
作者:Youzhi Luo,Yuchao Lin,Yi Liu,Shuiwang Ji
除了小分子和蛋白质之外,AI方法已经用于建模晶体材料,这是另一类由3D空间中原子的周期重复形成的大型化合物家族。晶体材料是许多实际工业应用的基础,如半导体电子学、太阳能电池和电池[Butler等人,2018]。由于行业的巨大需求,材料科学已经涌现出来,用于研究各种基础研究,如预测材料性质(例如形成能)和设计具有目标性质的新材料。长期以来,这些问题的研究进展相对较慢,因为它们严重依赖于昂贵的实验室实验或耗时的材料模拟。最近,受到AI方法的成功启发,特别是分子上的机器学习模型,许多研究已经尝试将这些模型应用于与晶体材料相关的问题[Choudhary等人,2023; Du等人,2023b]。然而,与分子不同,晶体材料中的原子排列具有复杂的重复单位单元和原子的周期排列。因此,晶体材料与分子具有非常不同的物理对称性,开发有效的AI模型需要明确地捕捉这些模型中的这些对称性。
在本节和接下来的节中,我们通过晶格矢量和其中一个单元格来描述晶体材料的结构,即最小的可重复结构。具体来说,如果任何单元格中的原子数为𝑛,则晶体材料M表示为M = (𝒛, 𝐶, 𝐿)。在这里,𝒛 ∈ Z𝑛是原子类型向量,其中𝒛的第𝑖个元素𝑧表示单元格中第𝑖个原子的原子类型(原子序号)。𝐶 = [𝒄1, ..., 𝒄𝑛] ∈ R3×𝑛是坐标矩阵,其中𝒄𝑖表示单元格中第𝑖个原子的3D坐标。𝐿 = [l1, l2, l3] ∈ R3×3是晶格矩阵,其中三个晶格矢量l1、l2、l3描述了原子沿其周期性重复的三个周期性矢量。在物理学中,晶体材料存在几种明确定义的对称性变换,包括以下几种置换、𝐸(3)和周期性变换。
• 置换变换通过对M = (𝒛, 𝐶, 𝐿)中的原子顺序进行排列,即交换𝒛中的元素和具有相同顺序的𝐶中的列向量,生成新材料。
• 𝐸(3)变换,或刚性变换,通过在3D空间中进行平移、旋转或反射来改变M = (𝒛, 𝐶, 𝐿)的3D坐标。具体来说,𝐶和𝐿被替换为𝑅𝐶 + 𝒕 1𝑇和𝑅𝐿,其中𝒕 ∈ R3是任意的平移向量,𝑅 ∈ R3×3是满足𝑅𝑇 𝑅 = 𝐼的正交矩阵,1是一个所有元素都为1的𝑛维向量。
• 周期性变换将M = (𝒛, 𝐶, 𝐿)的3D坐标映射到周期性等效的坐标,可以形式上描述为用新的坐标矩阵𝐶′ = 𝐶 + 𝐿𝐾替换𝐶,其中𝐾 ∈ Z3×𝑛是任意的整数矩阵。
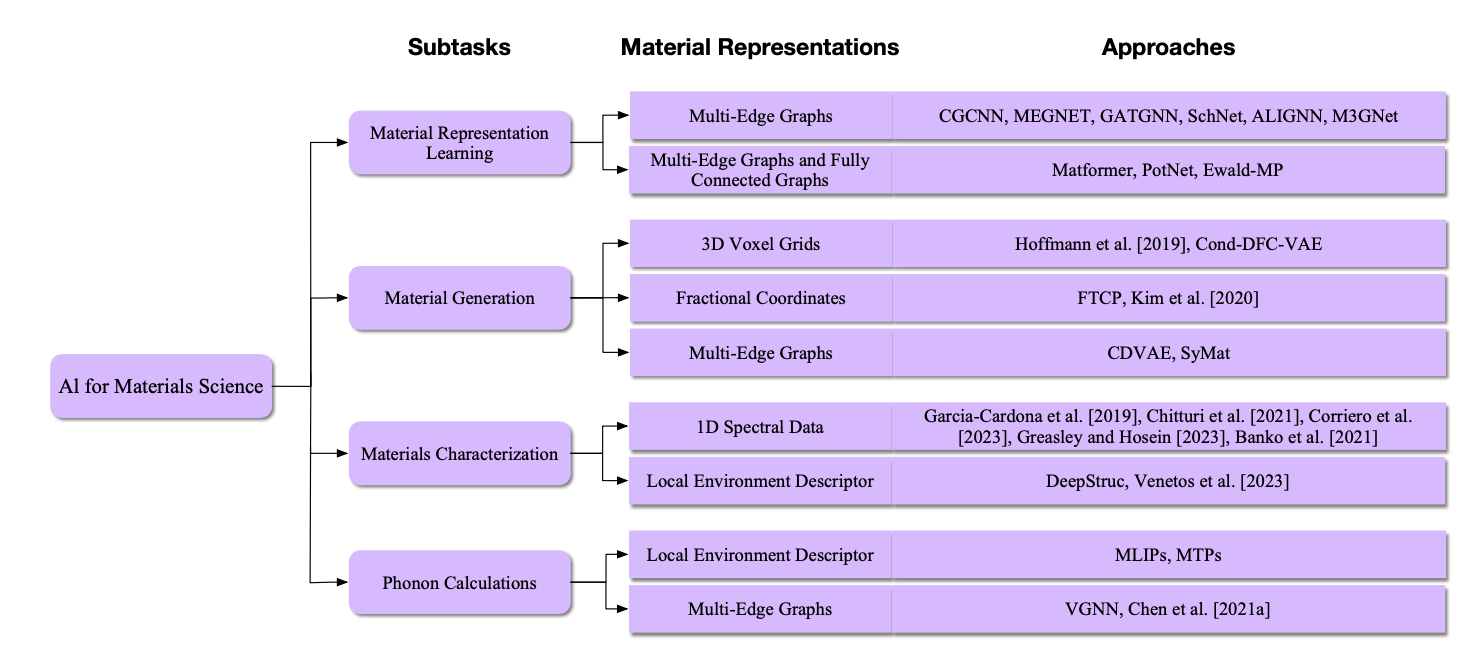
图28. 材料科学中AI任务和方法的概述。在这一部分,我们考虑了四个任务,包括材料表示学习、材料生成、材料表征和声子计算。在材料表示学习中,我们讨论了使用不同的材料图表示的两类方法。第一类方法包括CGCNN [Xie和Grossman 2018]、MEGNET [Chen等人 2019b]、GATGNN [Louis等人 2020]、SchNet [Schütt等人 2018]、ALIGNN [Choudhary和DeCost 2021]和M3GNet [Chen和Ong 2022],只使用多边图。第二类方法包括Matformer [Yan等人 2022]、PotNet [Lin等人 2023d]和Ewald-MP [Kosmala等人 2023],使用多边图和完全连接图来捕获周期性信息。在材料生成中,我们讨论了三类使用三种不同的3D材料结构表示作为生成目标的方法。第一类方法包括Hoffmann和Noé [2019]和Cond-DFC-VAE [Court等人 2020],生成3D体素网格。第二类方法包括FTCP [Ren等人 2022]和Kim等人 [2020],生成分数坐标。第三类方法包括CDVAE [Xie等人 2022a]和SyMat [Luo等人 2023c],以多边图的形式生成材料。在材料表征中,我们讨论了使用不同材料表示的两类方法。第一类方法包括Garcia-Cardona等人 [2019]、Chitturi等人 [2021]、Corriero等人 [2023]、Greasley和Hosein [2023]以及Banko等人 [2021],使用1D光谱数据表示材料,然后预测材料结构。第二类方法包括DeepStruc [Kjær等人 2023]和Venetos等人 [2023],利用材料的局部环境描述符来建模无序材料。请注意,第7.4节和第7.5节都描述了材料表征,而第7.5节特别针对无序材料的情况。为了清晰起见,在此图中,这两节已经合并成一个任务,即材料表征。在声子计算中,我们讨论了使用不同材料表示的两类方法。第一类方法包括MLIPs [Mortazavi等人 2020]和MTPs [Zuo等人 2020],应用材料的局部环境描述符来表示材料结构。第二类方法包括VGNN [Okabe等人 2023]和Chen等人 [2021a],使用多边图来捕获周期性信息。
换句话说,对于任意材料M = (𝒛, 𝐶, 𝐿),如果通过对M应用上述变换之一得到M′,我们应该将M和M′视为同一材料的不同表示。理想情况下,学习的属性预测函数𝑓和材料分布𝑝应该具有对称性感知,即满足𝑓(M) = 𝑓(M′)和𝑝(M) = 𝑝(M′)。在接下来的小节中,我们将回顾和讨论现有的用于材料表示学习和材料生成的AI方法,以及包括有序/无序材料表征和声子计算在内的新兴主题,主要从捕获对称性的角度进行比较。请参见我们所涵盖的方法的概览,见图28。
7.2 材料表示学习
作者:Keqiang Yan、Yuchao Lin、Youzhi Luo、Yi Liu、Shuiwang Ji 推荐先修知识:第7.1节
本节首先讨论了用于属性预测的材料表示学习。开发材料表示学习模型的主要挑战在于捕捉晶体材料的对称性,特别是对周期性变换的不变性。为了克服这一挑战,现有研究提出了许多晶体图表示构建方法和晶体图神经网络模型。我们将在下面的小节中详细介绍它们。
7.2.1 问题设置
材料表示学习需要学习一个函数𝑓来预测给定材料M的属性𝑦,其中𝑦可以是一个实数(回归问题)或分类号(分类问题)。
7.2.2 技术挑战
晶体材料表示学习旨在基于它们的晶格结构来预测晶体材料的物理和化学性质。如上节所述,不同于小分子或蛋白质,晶体材料由最小单位晶胞结构和相应的3D空间中周期性重复的模式组成。因此,需要为晶体材料建立独特的几何对称性和模型设计。具体而言,当对𝐶和𝐿同时应用旋转变换,或仅对𝐶应用平移变换时,晶体结构保持不变,这是由Yan等人[2022]描述的晶胞𝐸(3)不变性。除此之外,当应用周期性变换时,晶体结构保持不变,相应的图表示应该是相同的,这是由Matformer[Yan等人2022]描述的周期不变性。此外,指示单位晶胞在3D空间中重复的方向的周期性模式对晶体结构建模也至关重要。对于晶体神经网络的设计,由于晶体结构中的一个单元格可以包含两百多个原子,考虑原子之间的高阶相互作用仍然具有挑战性。然而,高阶相互作用可以被认为是不可或缺的,以实现晶体结构的完整几何表示。此外,需要为晶体结构设计强大且高效的网络,因为一个单元格中可能有两百多个原子。
7.2.3 现有方法
如图29所示,材料表示学习的典型流程包括构建晶体图表示和使用晶体图神经网络来预测属性。我们将在下面讨论几种代表性的晶体图表示方法和晶体图神经网络模型。
晶体图表示:晶体的周期性特性为晶体表示学习提出了独特的挑战,如上所述。具体来说,为了解决挑战(1)和(2),CGCNN [Xie和Grossman 2018]提出通过基于单位晶胞结构构建的多边晶体图来表示无限的晶体结构,这已被Yan等人[2022]证明是周期不变的。具体地,多边晶体图将给定的原子和其在3D空间中的所有副本映射为单个节点,并通过记录成对欧几里德距离作为多条边来建模节点对之间的相互作用。由于多边晶体图的有效性和简单性,它已经被许多后续工作广泛使用,包括MEGNET [Chen等人 2019b],通过记录成对的欧几里德距离,多边晶体图能够保持对𝐸(3)变换的不变性,包括3D空间中的旋转、平移和反射。因此,多边晶体图具有周期不变性和𝐸(3)不变性,仅考虑了二阶的成对欧几里德距离。除此之外,为了启用更高阶的相互作用,ALIGNN提出了在不破坏周期不变性的情况下进一步包括键之间的角度,而M3GNet以类似的方式包括了三体相互作用。然而,这些方法只考虑了给定原子的局部相互作用,无法捕获周期性模式,这是晶体结构与分子结构之间的关键区别。为了明确捕获周期性模式,Matformer[Yan等人 2022]提出使用六个自连接边来编码三个周期矢量,它们的组合可以完全捕获周期矢量的长度和它们之间的角度。此外,最近的两项工作利用Ewald求和来捕获周期信息。PotNet[Lin等人 2023d]提出通过使用多种类型的势能的无限求和来考虑晶体结构中任意两个节点之间的无限相互作用,因此,这些求和捕获了周期模式。在类似的思路下,Ewald-MP[Kosmala等人 2023]通过应用Ewald求和中的分解来解决周期结构中的长程相互作用问题。通过将消息传递的聚合分解为在实空间中建模的短程信号和在傅里叶空间中建模的长程信号,明确捕获了周期结构信息。前期工作的晶体图表示总结如表25所示。
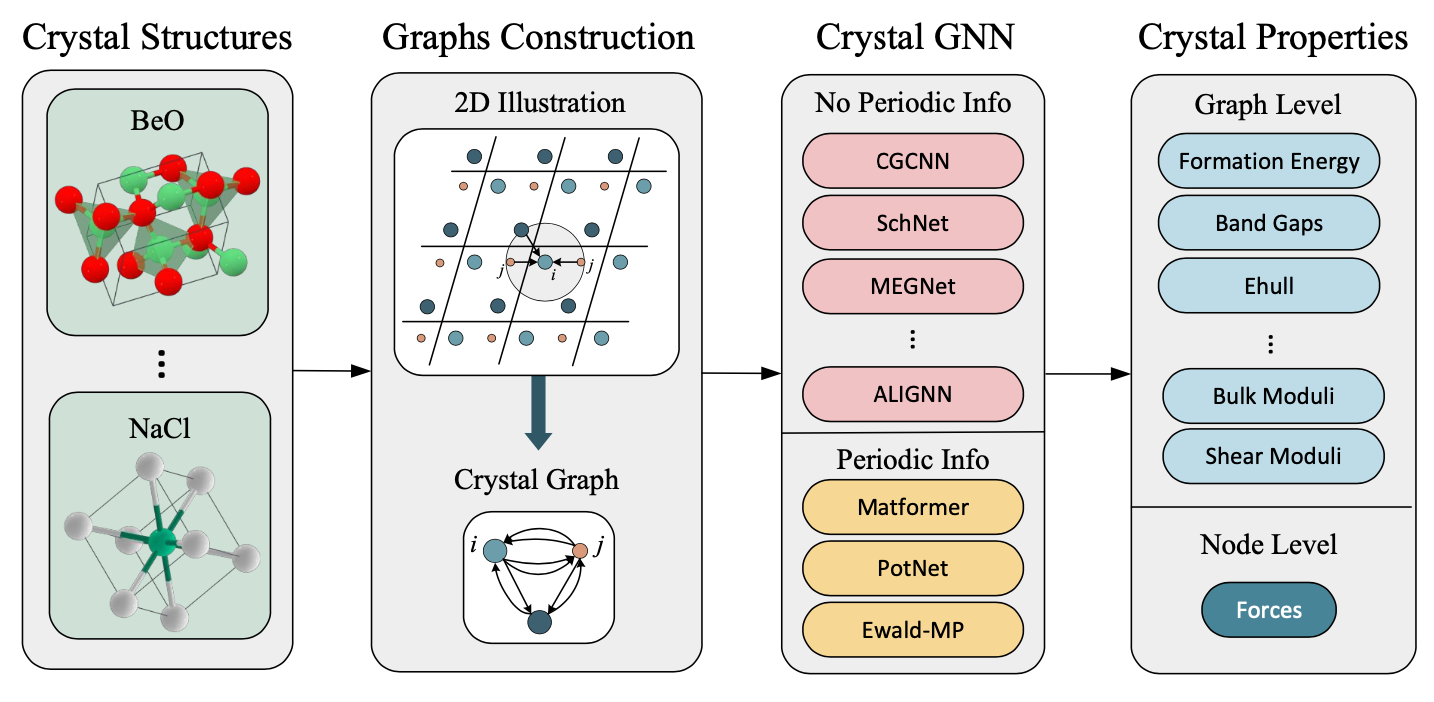
图29. 材料表示学习的流程。晶体材料被转化为晶体图表示,随后作为晶体图消息传递神经网络的输入。然后,模型被训练以准确预测晶体的所需性质。值得注意的是,消息传递过程可以根据其是否包含周期性信息来区分,比如晶格长度或无限势能求和。不包含周期信息的网络包括诸如CGCNN [Xie和Grossman 2018]、SchNet [Schütt等 2018]、MEGNet [Chen等 2019b]和ALIGNN [Choudhary和DeCost 2021]等模型。相反,包含周期信息的网络包括Matformer [Yan等 2022]、PotNet [Lin等 2023d]和Ewald-MP [Kosmala等 2023]等模型。此外,预测的输出可以被分类为图级别属性,包括形成能和带隙,或节点级别属性,包括力。
表25. 摘要了以前工作使用的晶体图表示。可以看出,所有以前的工作都满足周期不变性并实现了𝐸(3)不变性。在这些方法中,Matformer [Yan等 2022]、PotNet [Lin等 2023d]和Ewald-MP [Kosmala等 2023]明确编码周期性模式。CGCNN [Xie和Grossman 2018]、MEGNET [Chen等 2019b]、GATGNN [Louis等 2020]、SchNet [Schütt等 2018]、Matformer [Yan等 2022]和PotNet [Lin等 2023d]只使用了两体键信息,而ALIGNN [Choudhary和DeCost 2021]和M3GNet [Chen和Ong 2022]还使用了三体角信息。

GATGNN [Louis et al. 2020] 和 ALIGNN [Choudhary 和 DeCost 2021] 是两种现代晶体图神经网络的代表。此外,采用成对的欧氏距离可以实现多边晶体图不受 𝐸(3) 变换的影响,包括在三维空间中的旋转、平移和反射。因此,多边晶体图具有周期性不变性和 𝐸(3) 不变性,仅考虑二阶体次的成对欧氏距离。除此之外,为了实现更高阶的相互作用,ALIGNN 提出了在不破坏周期性不变性的情况下进一步包括键之间的角度,而 M3GNet 以类似的方式包括三体相互作用。然而,这些方法仅考虑给定原子的局部相互作用,不能捕捉周期性模式,而晶体结构和分子结构之间的关键差异就在于此。为了明确捕捉周期性模式,Matformer [Yan et al. 2022] 提出使用六个自连接边来编码三个周期向量,它们的组合可以完全捕捉周期向量的长度和它们之间的角度。此外,最近的两项工作利用 Ewald 求和来捕捉周期性信息。PotNet [Lin et al. 2023d] 提出通过使用多种类型势能的无限求和来考虑晶体结构中任意两个节点之间的无限相互作用,从而通过这些求和来捕捉周期性模式。在类似的思路下,Ewald-MP [Kosmala et al. 2023] 通过将消息传递的聚合分解为在实空间建模的短程信号和在傅里叶空间建模的长程信号来解决周期性结构中的长程相互作用问题,从而明确地捕捉周期性结构信息。前述工作的晶体图表示的摘要如表 25 所示。
晶体图神经网络:现代图神经网络在预测材料性质方面的有效性依赖于它们融入的对称性和高阶信息,以及所使用的消息传递方式。现有的网络,如 CGCNN [Xie 和 Grossman 2018]、MEGNET [Chen et al. 2019b]、GATGNN [Louis et al. 2020] 和 SchNet [Schütt et al. 2018],采用半径晶体图,在消息传递期间仅考虑二体距离作为边的特征,类似于分子表示学习中使用的方法。具体而言,SchNet 和 MEGNET 使用常见的图卷积网络,而 CGCNN 则采用 sigmoid 门操作对节点和边的特征进行连接,而 GATGNN 在消息传递期间使用注意力机制来加权节点特征。此外,如上所述,Matformer [Yan et al. 2022]、PotNet [Lin et al. 2023d] 和 Ewald-MP [Kosmala et al. 2023] 在消息传递期间包括额外的特征,以解决先前方法缺乏周期性信息的限制。具体而言,Matformer 明确地将晶格结构信息编码为自连接边。此外,PotNet 通过将长程和短程相互作用相加并将它们编码为全连接图的边特征,考虑了无限的原子间势能求和。相比之下,Ewald-MP 将长程相互作用与短程消息传递分离,并在每一层之后将短程和长程节点嵌入组合在一起。为了降低与全连接图相比的复杂性,这两种消息传递都建立在截断图上,即在实空间中有一个距离截断和在傅里叶空间中有一个频率截断。虽然大多数上述方法都基于原子间(二体)信息,但包括三体信息也可以增强材料表示,正如 ALIGNN [Choudhary 和 DeCost 2021] 和 M3GNet [Chen 和 Ong 2022] 所展示的那样。这些方法将晶体图转换为线图,其中原始边变为节点特征,边之间的角度变为边特征。然后,它们随后应用图神经网络,类似于 CGCNN,来学习材料表示。
7.2.4 数据集与基准。
表 26 中显示了三个广泛使用的晶体性质预测基准,包括 Materials Project-2018.6.1 [Chen et al. 2019b]、JARVIS [Choudhary 和 DeCost 2021] 和 MatBench [Dunn et al. 2020]。Materials Project-2018.6.1 包括四个广泛使用的回归任务,涉及形成能、带隙、体积模量和剪切模量等性质。JARVIS 包括 29 个晶体性质回归任务和 10 个晶体性质分类任务。JARVIS 中广泛使用的回归任务包括形成能、带隙(OPT)、带隙(MBJ)、Ehull 和总能量。MatBench 包括 10 个回归任务和 3 个分类任务。大多数晶体性质是通过基于密度泛函理论(DFT)的方法计算得出的。
表26。 Materials Project-2018.6.1(MP)[Chen等,2019b]、JARVIS [Choudhary和DeCost,2021]和MatBench [Dunn等,2020]的数据集统计信息。总结了对应数据集中最大规模任务中的晶体数量、回归任务数量和分类任务数量。

7.2.5 开放性研究方向。
首先,目前基于深度学习的晶体性质预测方法主要针对回归和分类任务设计。未来的一个可能方向是探索更高阶的旋转晶体性质,包括原子力、介电张量等。其次,目前用于晶体性质预测任务的现有方法在几何上并不完备,对于无限晶体结构的几何完整性是一个具有挑战性但重要的课题。
7.3 材料生成
作者:Youzhi Luo, Shuiwang Ji 推荐先修课程:第 7.1 节
在这一部分中,我们关注生成晶体材料的问题。在这个问题中,一个关键挑战是在生成模型的概率建模框架中实现对所有对称性变换的不变性。在以下各小节中,我们详细介绍了几种现有的晶体材料生成方法及其捕获的对称性。
7.3.1 问题设置。
材料生成学习一个概率分布 𝑝,以便通过从 𝑝 中抽样生成新材料。
7.3.2 技术挑战。
对于晶体材料生成问题,我们的目标是通过生成模型学习材料空间上的概率分布 𝑝,并从 𝑝 中抽样生成新的晶体材料。这个问题的关键挑战是将所有晶体材料的对称性纳入到生成模型中。换句话说,如果两个晶体材料 𝑀 和 𝑀′ 可以通过对称变换互相转化,生成模型应该为它们分配相同的概率。特别地,3D 材料结构的对称变换包括不仅包括在其他化合物中常见的𝐸(3) 变换,还包括晶体材料独有的周期性变换。因此,我们不能简单地将现有的3D分子生成方法(第5.4节)应用于晶体材料生成问题,因为它们不考虑对周期性变换的不变性。将不变性引入到现有的3D分子生成的 𝐸(3) 不变的生成模型中,面临着重大挑战。此外,周期性变换不会保持每对两个原子之间的距离,因此它们不是欧几里得变换。因此,我们不能使用3D特征,如距离、角度或扭转角,作为生成目标来生成3D材料结构。
7.3.3 现有方法。
通常,有两种策略可以用来确保对周期性变换的不变性。首先,我们可以通过生成3D特征或表示(例如3D体素网格),这些特征在内部对周期性变换具有不变性,从而隐式确定材料中的原子位置。使用这种策略的两种代表性方法是 Cond-DFC-VAE [Court等,2020] 和Hoffmann等人提出的方法 [2019]。它们都将晶体材料转换为3D体素网格,将3D体素网格平滑到3D密度图,并将3D密度图用作生成目标。具体来说,从3D晶体材料中提取所有原子在3D立方体中的信息,可以得到3D体素网格。对于3D体素网格中的任何网格点,如果其对应位置有原子,则其体素值为非零,非零体素值包含原子类型的信息。由于3D体素网格通常非常稀疏且不适合作为直接的生成目标,因此它们被平滑到大多数值为非零的3D密度图。晶体材料是通过首先使用VAE模型 [Kingma和Welling,2014] 生成3D密度图,然后使用U-Net模型 [Ronneberger等人,2015] 将其分割成3D体素网格来生成的。3D体素网格或3D密度图对周期性变换具有不变性,但不对𝐸(3) 变换具有不变性,因此Cond-DFC-VAE和Hoffmann等人的方法 [2019] 都无法捕捉𝐸(3) 对称性。
此外,另一种策略是直接生成晶格矩阵 𝐿 和坐标矩阵 𝐶,但需要为生成模型定制概率建模,以便对于任意整数矩阵 𝐾 ∈ Z3×𝑛,𝑝(𝐶) = 𝑝(𝐶 + 𝐿𝐾) 始终成立。两种早期方法,FTCP [Ren等,2022] 和 Kim等人的方法 [2020],提出生成晶格参数和分数坐标矩阵。具体来说,晶格参数是三个晶格向量的L2范数和每两个晶格向量之间的角度,对于晶体材料 𝑀 = (𝒛,𝐶,𝐿),其分数坐标矩阵被定义为 𝐹 = 𝐿−1𝐶。可以很容易地证明晶格参数和分数坐标矩阵对旋转和反射变换是不变的。然而,分数坐标矩阵假定原子之间有一定的顺序,因此它们不是置换不变的,也不对平移和周期性变换具有不变性。与直接生成分数坐标矩阵不同,最近的两种方法,CDVAE [Xie等,2022a] 和SyMat [Luo等,2023c],提出以3D图的形式生成晶体材料。它们使用VAE模型生成上述的晶格参数,随机初始化原子坐标,并通过得分匹配模型 [Song和Ermon,2019] 迭代地优化原子坐标。特别是,在这两种方法中,原子坐标的优化是通过多边图 [Xie和Grossman,2018] 上的𝐸(3)-等变图神经网络模型完成的,多边图是晶体材料的3D图表示。由于多边图不假设原子的顺序并且对周期性变换具有不变性,它们对原子坐标优化的概率建模确保了对置换和周期性变换的不变性。尽管这些相似之处,CDVAE 和SyMat在坐标优化过程中针对不同的目标应用得分匹配。CDVAE直接将得分匹配应用于原子坐标,无法实现平移不变性。与此不同,SyMat将得分匹配应用于原子之间的成对距离,以实现对所有 𝐸(3) 变换的不变性。我们在表27中总结了本节讨论的所有晶体材料生成方法的关键信息和捕获的对称性。
7.3.4 数据集与基准。
长期以来,材料生成任务没有标准的基准数据集。早期的材料生成方法通常在Materials Project数据库 [Jain等,2013] 或其他数据库中手动选择的材料上进行评估。直到最近,Xie等人 [2022a] 为不同的材料生成方法的评估策划了三个基准数据集,分别是Perov-5、Carbon-24和MP-20。Perov-5数据集从一个用于水分解的开放材料数据库 [Castelli等,2012b,a] 中收集了18,928种钙钛矿材料。Perov-5中的所有材料都具有一个晶胞中的5个原子。Carbon-24数据集收集了10,153种材料,它们的3D结构在10 GPa下经过AIRSS [Pickard和Needs,2006,2011] 优化。Carbon-24中的所有材料仅包含碳原子,并且一个晶胞中最多包含24个原子。MP-20数据集由45,231种材料组成,其能量高于壳层且形成能小于0.08 eV/原子和2 eV/原子。MP-20中的所有材料都来自Materials Project数据库,一个晶胞中最多包含20个原子。有关这三个数据集的一些统计信息,请参见表28。
表27. 总结了几种代表性的晶体材料生成方法中的3D输出、模型架构以及捕获的对称性。在这些方法中,Hoffmann 和 Noé [2019] 以及Cond-DFC-VAE [Court et al. 2020] 生成3D体素网格,对于置换和周期性变换具有不变性,但对于旋转、反射和平移不具有不变性。FTCP [Ren等,2022] 和 Kim 等人 [2020] 生成分数坐标,只对旋转和反射具有不变性。CDVAE [Xie等,2022a] 和SyMat [Luo等,2023c] 以多边图的形式生成材料。它们都实现了对置换、旋转、反射和周期性变换的不变性。然而,由于直接将得分匹配应用于坐标,CDVAE 未能实现对平移的不变性,而SyMat 实现了这一点,因为它将得分匹配应用于成对距离。

表28. Perov-5、Carbon-24 和 MP-20 数据集的一些统计信息 [Xie等,2022a]。我们总结了3D分子样本的数量 (# 样本)、一个分子中的最大原子数 (最大 # 原子) 和一个分子中的平均原子数 (平均 # 原子)。

7.3.5 开放性研究方向。
尽管最近提出了几种晶体材料生成方法,但仍然存在一些未解决的挑战,阻碍了它们的实际应用。首先,包括CDVAE和SyMat在内的最近方法基于得分匹配模型。它们在性能上比早期方法更好,但通过得分匹配模型在成千上万次迭代中优化原子坐标需要更高的计算成本。在实际应用中,希望能够设计一种高效的生成模型,以合理的时间成本生成优质的材料样本,但设计这样的模型仍然具有挑战性。其次,确保模型生成的晶体材料在实际合成中可行是很重要的。然而,据我们所知,文献中尚未使用标准的评估指标来衡量生成模型生成的晶体材料的可合成性。引入这种可合成性指标可以帮助过滤出不能实际合成的材料,而且设计能够优化其生成材料的可合成性指标的新型材料生成方法也具有趣味性但也具有挑战性。
7.4 材料表征
作者:Elyssa F. Hofgard、Aria Mansouri Tehrani、Yuchao Lin、Tess Smidt 推荐先修内容:第 7.1 节
在最后两节中,我们描述了基于晶体结构预测材料性质的机器学习方法,以及生成新的晶体结构。然而,也许更基本的挑战是准确和高效地实验确定晶体结构。除了长程有序性外,从非晶材料的短程有序到Prussian Blue类似材料的相关随机性,各种局部随机性可能会出现并影响材料的性质 [Simonov和Goodwin 2020; Kholina等 2022]。因此,为了确定材料的确切晶体结构,通常需要使用X射线和中子散射以及光谱等仪器和表征技术的组合。
这些测量通常在实验室或大型设施(例如,同步辐射束线)中进行,需要耗时和谨慎地对数据进行建模。为了更好地理解,现代X射线探测器可以每天生成多达100万张图像,数据后处理、实验分析和解释可能需要超过一年的时间 [Doucet等 2020; Chen等 2021b; Wang等 2017b]。机器学习方法处理大数据、在复杂数据中找到模式以及计算机视觉算法用于自动检测图像等能力可以在加速实验过程中发挥重要作用,为束线用户设施提供实验期间的即时反馈 [Wang等 2017b; Doucet等 2020; Sullivan等 2019; Yanxon等 2023; Wang等 2017b; Banko等 2021; Özer等 2022; Venderley等 2022]。
在这里,我们讨论了将机器学习方法与表征技术集成的一些挑战和机会。我们具体回顾了使用散射和光谱技术来预测平均和局部晶体结构(以及它们的逆问题)的现有工作。需要注意的是,由于表征方法的巨大变化和复杂性,我们只是触及了可能性的表面。
7.4.1 问题设置。
如概述中所讨论的,由于材料表征方法的内在多样性,机器学习在材料表征方法中的潜在应用非常广泛。因此,我们将问题设置重点放在了两个主要类别中:
• 晶体结构预测:这个类别涉及使用实验性表征技术的输出,如X射线衍射的一维(1D)光谱,来预测三维(3D)晶体结构,其中包括原子位置以及三个晶格向量或其他晶体结构参数,如晶体系统、Bravais晶格类型、晶胞长度和晶胞角度。
• 其逆问题:前述过程的逆过程形成了第二类问题,即使用晶体结构来预测表征方法的输出。
例如,使用材料的晶体结构,如原子位置和晶格向量,来重构一维(1D)和二维(2D)衍射光谱。
7.4.2 技术挑战。
从散射图案中重构三维晶体结构或相关参数的过程并不是简单的。散射信号可以由复杂的波函数描述,其中振幅表示散射的幅度,相位表示散射中心的位置和排列。然而,在实践中,通常只测量或记录强度(振幅的平方)。没有相位信息,衍射图案可能无法唯一地映射到晶体结构,反之亦然。这被称为相位问题)[Sivia等 1991]。问题更加复杂,因为散射数据是按材料基础获取的。实验数据可能因材料、样品质量以及实验者所提出的科学问题而异。因此,每次实验可能存在多种数据模态。因此,开发能够适应实验数据以及模拟数据的机器学习模型非常关键。
正如本节前面所述,晶体是周期性且高度对称的结构。例如,对于从晶体结构重构散射数据的逆问题,应该保留等变性(例如,将晶体对称性群的元素应用于输入将导致相同的散射输出)。因此,这些问题需要设计保持对称性和等变性的机器学习方法,这是一项具有挑战性的任务。
7.4.3 现有方法。
以谱数据作为输入:首先,我们描述了将谱数据作为机器学习算法输入的现有工作。大多数现有工作将其用于分类晶体对称性(晶体类别、勃拉维格点或空间群)或在回归问题中找出晶体晶格参数。晶体材料的结构可以由三个晶格矢量和一个单位胞来描述。单位胞可以根据六个晶格参数来指定,这些参数是单元胞边缘的长度(∥l1∥,∥l2∥,∥l3∥)以及它们之间的角度(𝛼,𝛽,𝛾)。在三维空间中,有七个晶体类别和14个勃拉维格点。
许多先前的研究已经使用CNN来进行晶格类型分类或晶格参数回归。Garcia-Cardona等人[2019]开发了一个CNN分类器,用于从中子散射数据中预测钙钛矿晶体系统和晶格参数{∥l1∥,∥l2∥,∥l3∥,𝛼,𝛽,𝛾}。然后,他们训练了每个研究的晶体学对称性的随机森林回归模型,以预测晶格参数。这两个模型对于较低对称度的晶体系统的准确性较低。他们得出结论,需要更复杂的模型来处理实验数据。Chitturi等人[2021]假设晶体系统已经知道,并使用1D CNN来预测每个晶体系统的晶格参数。1D CNN能够预测出单位胞的长度,但无法预测单斜晶体或三斜晶体系统(较低对称类别)的单位胞角度。Corriero等人[2023]也使用CNN和随机森林来预测晶体系统和空间群。
虽然CNN可能是一个常见的选择,但Greasley和Hosein[2023]证明了更传统的监督学习算法,如支持向量机(SVM)和补充朴素贝叶斯(CNB)分类器,在多相识别方面与神经网络一样表现出色,而且适用于实验和模拟XRD谱。其他研究小组也采用了变分自编码器(VAE)架构。VAE的潜变量空间是训练样本的“压缩”表示,因此这可以是从散射数据中学习材料性质的有意义的连续表示的有效策略。例如,Banko等人[2021]发现,潜变量空间提供了编码器模型的聚类属性和XRD图案中主要反射轴的分布的直接可视证据。
然而,必须注意的是,这些方法都将1D谱作为输入。例如,CNN假定输入数据中存在平移不变性,这可能在这些谱中不存在。因此,在将它们应用于粉末谱之前,应考虑ML模型的对称性和假设。此外,值得开发更有意义地利用等变性的方法。
以谱数据作为输出:使用结构或其他物理性质来预测衍射图案等反问题,尚未广泛使用ML技术进行研究。Cheng等人[2023b]开发了一种基于ML的框架,可以从结构(原子坐标和元素种类)预测一维和二维非弹性中子散射(INS)谱。这项研究扩展了Chen等人[2021a]的工作,使用等变神经网络来预测声子态密度。他们首先使用自编码器来表示潜变量空间中的2D谱(动量和能量转移的函数),否则在动量/能量空间中将有300 x 300的图来预测。然后,他们使用欧几里德神经网络来预测潜变量空间中的特征,并重构2D谱。请注意,此方法也可以应用于1D谱,可能不需要自编码器步骤。因此,等变神经网络代表了从晶体结构重构谱数据等反问题的有前途的途径。
7.4.4 数据集和基准。
由于缺乏可用的实验数据,使用合成数据来训练X射线/中子散射的机器学习模型是不可避免的。然而,实验数据通常与模拟数据相当不同。包含结构信息的模拟数据集包括Materials Project [Jain et al. 2013]、无机晶体结构数据库(ICSD)[D et al. 2019]和剑桥晶体数据库(CSD)[Groom et al. 2016]。开发更具一般性的模型的一种方法是对模拟数据进行数据增强,以解决可能的实验因素,如峰移、展宽、纹理和噪声背景。另一种方法是在模拟数据上进行训练,但在实验数据上进行测试(如预期的那样,通常不会产生令人满意的结果)。据我们所知,由于涉及的实验设置和问题种类繁多,不存在用于评估X射线/中子散射的机器学习算法性能的实验数据集。为了开发稳健的机器学习方法,应创建此类基准数据集。
7.4.5 开放研究方向。
在未来,构建利用对称性和傅立叶变换原理来有效表示实空间、倒空间或两者中的散射数据的模型将非常有用。散射实验的一个常见主题是在倒空间中获取数据,以提供有关传统上在实空间中表示的某些信息。已经开发了在频率域操作的神经网络。Li等人[2021b]开发了一个在傅立叶空间中定义的神经网络架构,而Yi等人[2022]将其扩展为在傅立叶域中执行图卷积。这种方法有可能与等变神经网络相结合,并应用于这个问题。由于存在相位问题,一个了解傅立叶空间并能够与实空间交换信息的等变神经网络可能非常强大。
另一个未来的方向可能是探索通过等变操作来表示材料的不同方式,以及这些方式与粉末谱的关系。这可能适用于不同的等变ML方法。总的来说,当前的模型在较低对称性结构(分类和预测晶格参数)以及实验数据方面表现较差,因此这些问题应该在未来的研究中加以解决。
7.5 本地结构和无序材料表征
作者:Aria Mansouri Tehrani、Tuong Phung、Yuchao Lin、Tess Smidt
推荐先修内容:第7.1节、第7.4节
在上一节中,我们讨论的晶体学方法对于创建平均原子位置的结构模型非常有用。然而,它们忽略了晶体材料可能存在随机或相关的无序性。已经证明,无序性存在并且显着影响晶体材料的性质[Simonov和Goodwin 2020;Kholina等 2022;Venetos等 2023;Cheetham等 2016]。此外,对于具有有限或没有长程有序性的材料,如纳米结构和非晶材料,短程有序性甚至更为重要[Li等 2020c;Martin等 2002]。探测局部结构的一种方法是使用原子对分布函数(PDF)分析,它是X射线、中子或电子衍射粉末或单晶样品的总散射的傅立叶变换[Young和Goodwin 2011;Kjær等 2023;Liu等 2019]。另外,光谱学分析,如核磁共振(NMR),可以提供关于局部结构的进一步见解[Venetos等 2023]。
7.5.1 问题设置。
在这个任务中,模型利用探测材料局部结构的表征技术的结果,例如原子对分布函数(PDF)和核磁共振(NMR),来预测或生成材料的结构,包括实验室坐标系内的三维(3D)原子位置[Kjær等 2023],或者与局部原子参考框架相对应的化学性质,例如NMR化学位移张量的大小、各向异性和方向[Venetos等 2023],该张量描述了核子受到其周围电子环境影响的方式。
7.5.2 技术挑战。
解决材料的短程有序性在实验和计算上都是极具挑战性的任务。例如,即使在DFT计算中引入小的无序性,如位点共享或点缺陷,也需要进行昂贵的大规模超胞计算以考虑许多不同的构型。对于非晶材料,这些计算几乎是不可能的,因此阻碍了为ML创建大量训练数据的可能性。因此,ML模型不能依赖标准的计算数据。不幸的是,短程有序性的实验表征也不是一件简单的事情。获得有关局部结构的见解的一些方法包括粉末衍射的PDF分析、单晶衍射的3D-ΔPDF建模(使用Yell计算程序),或将散射和光谱技术相结合[Simonov等 2014;Venetos等 2023]。总散射技术需要大量的相纯粉末样品,适合中子或高质量的单晶样品,大型设施的高强度中子或X射线源,进行实验的领域和光束线专家,以及对漫射散射的繁琐精炼。在ML方面,因此至关重要的是构建能够有效捕捉局部原子结构的表示,开发数据高效且能够预测张量性质的模型。
7.5.3 现有方法。
从原子对分布函数中从头解决晶体结构是极其具有挑战性的,到目前为止,只有对高度对称的纳米结构进行了此类工作[Juhás等 2006]。最近的工作开发了一种称为DeepStruc的深度生成模型,可以使用条件变分自编码器直接从PDF解决简单的单金属纳米颗粒结构[Kjær等 2023]。PDF,也被称为𝐺(𝑟),代表了实空间原子间距的直方图,定义为:【PDF的数学公式未提供】
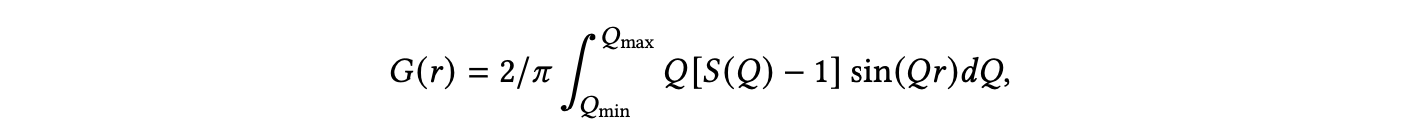
其中𝑄是散射矢量,𝑆(𝑄)是总散射结构函数,它依赖于测得的X射线散射强度和原子形状因子。而单金属纳米颗粒的结构表示为图形,G=(𝑋,𝐴),其中𝑋∈R𝑁×3。在这里,𝑋是节点特征矩阵,原子间的连接由邻接矩阵𝐴∈R𝑁×𝑁描述。基于这一基础,他们利用条件深度生成模型来合成PDF条件下的数据,通过解决未分配距离几何问题(uDFO),本质上捕获了原子结构与PDF之间的关系。最后,他们通过使用实验数据展示,他们的模型能够成功预测一些简单单金属纳米颗粒的晶体结构[Juhás等 2006]。
除了散射技术,核磁共振(NMR)是一种强大的光谱学工具,通常与粉末X射线衍射一起使用,以阐明材料的局部环境。NMR化学位移张量既编码了由化学位移表示的原子的平均电子环境,也包含包含额外结构数据的各向异性。这些各向异性通过NMR测量中的线型可以明显观察到,并可用于推断局部化学键[Venetos等 2023]。利用等变几何深度学习方法的进展,直接预测张量性质并保留输入对称性,研究人员最近开发了一个模型来预测硅化合物中的Si化学位移张量[Venetos等 2023]。在这项工作中,使用MatTEN软件包实现了旋转等变性,该软件包利用了张量场网络和e3nn,同时为了进行比较,还构建了具有对称性不变性的模型。结果显示,等变模型的性能比对称性不变模型高出53%,突显了等变几何深度学习模型在预测表征测量中的对称性相关张量性质方面的应用。
7.5.4 数据集和基准。
由于在这一专业领域缺乏广泛承认的基准,数据集通常是通过模拟和自动生成来开发ML模型的。一个例子是PDF数据集[Kjær等 2023],其中通过原子模拟环境(ASE)生成了共计3742个单金属纳米颗粒的结构以及相应的PDF。特别包括了七种单金属纳米颗粒结构,如简单立方(sc)、体心立方(bcc)和面心立方(fcc)等。这些构造跨越了从5到200个原子的大小范围。此外,Venetos等人[2023]使用了由Sun等人[2020]计算的放松结构的一部分从头计算的NMR化学位移张量子集,其中包括421个独特的硅酸盐结构,1387个独特的硅位点以及不同数量的桥氧原子。这些例子强调了未来可以创建更全面数据集的机会,这将有助于推动这一领域的研究。
7.5.5 开放研究方向。
由于材料中的局部原子环境在确定其整体性质方面起着重要作用,因此了解局部环境几何与材料性质之间复杂的相互作用对于设计具有所需性质的下一代材料至关重要。我们希望有一种局部环境描述符,它对于同一种原子的平移、旋转和排列不变性是不变的,因为这些对称操作不会改变物理性质。
此外,最近的工作引入了一种称为局部预测刚度(LPR)的度量标准,以评估全局数量在多大程度上可以严格地分配给局部、以原子为中心的贡献[Chong等 2023]。

从这个函数中,通过将该函数展开成其球谐系数,可以得到一个球谐信号𝒙,如下所示:
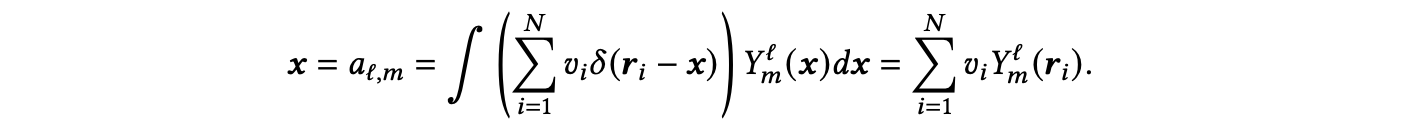
利用这个球谐信号𝑥,可以通过计算重复的对称张量积(𝑥⊗(𝑑+1))并提取标量和伪标量系数(𝒙⊗(𝑑+1) −→ (0,𝑒)⊕(0,𝑜))来计算阶数为𝑑的光谱。其中,第一、第二和第三阶光谱通常被称为功率谱、双谱和三谱,分别。双谱特别适用于表征局部环境,比功率谱更具表现力,但计算成本比三谱低。
光谱还具有其他良好的性质,包括平滑性(原始几何的小扰动导致结果光谱的小扰动)、可逆性(原始几何可以解码,但可能存在全局旋转)、固定长度(对于给定的𝑙值)。它们还可以进行聚类(例如,使用k均值聚类),从而可以识别给定材料类别内或不同材料类别之间的几何趋势。
除了进一步开发适当的、具有表现力的局部表示之外,未来的一个重要方向是利用ML的力量加速对无序材料的耗时表征过程。例如,计算机视觉可以用于快速检测布拉格峰的形状,进行校正和识别伪影等,而在某些情况下,可以利用等变神经网络的可靠性来保留对称性,以融入领域知识。
7.6 声子计算
作者:Adriana Ladera、Tess Smidt
推荐先修内容:第7.1节
声子是晶格振动的能量量子化,类似于光子是电磁波的量子化[Kittel 2004]。对这些声子的计算对于理解材料的热性和动力学性质至关重要。由于高效的密度泛函理论(DFT)代码和高性能计算的进展,第一原理声子计算已经变得非常可行,但是有效声子计算仍然存在实验和计算上的挑战。在本节中,我们详细说明了当前的障碍(力预测精度、有限资源、晶体学材料的周期性复杂化训练数据和当前模型的学习),现有方法(用于直接预测声子态密度的等变神经网络,基于从头分子动力学轨迹训练的矩张量势),以及在声子研究中整合ML的有前途的未来方向。
7.6.1 问题设置。
在声子计算中,需要提供晶体结构,包括原子位置、原子种类和晶胞的晶格矢量,以计算声子性质,这包括声子色散关系(通常称为声子带结构)和声子态密度(PDOS)等计算。声子带结构将声子动量与每个分支中的声子角频率相关联,通常沿布里渊区中的高对称路径。它对于研究声子相关性质非常重要,如声子-声子相互作用和电子-声子耦合,在热传输和电子输运中具有应用。声子态密度通过对波矢积分和对每个分支求和来总结声子色散。形式上,声子态密度定义为:
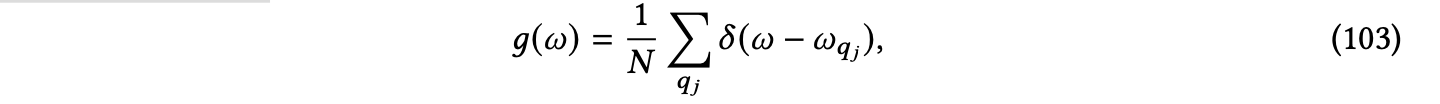
其中,𝑁是晶体中的晶胞数,𝑞是波矢,𝑗是能带索引,𝜔𝑞𝑗是声子频率[Togo和Tanaka 2015]。声子态密度对于理解多种材料性质非常重要,如超导性、电输运和振动性能。在预测声子态密度、声子带结构等声子计算时,图神经网络模型通常除了原子位置、质量和原子种类之外,没有关于原子间力和其他特性的先验知识,而在ML原子间势(MLIPs)中,模型是在从头分子动力学轨迹上训练的。
7.6.2 技术挑战。
对于研究热性质和声子带结构,DFT模拟提供了精确的近似,但在纳米孔隙和低对称性材料的情况下,计算成本会迅速增加。为了绕过计算约束,通常采用较低的k点网格、较小的超胞和平面波截止能量,但不出所料,这会导致生成的声子带结构的精度较低。此外,计算条件仍然可能在声子色散图中产生非物理频率[Mortazavi等 2020]。通过实验和计算方法获取声子态密度存在挑战,因为复杂材料的从头计算需要高计算成本,并且无弹性散射通常需要有限的资源[Chen等 2021a],例如高通量中子源或同步辐射X射线[Hanus等 2021]。
材料科学中的机器学习的若干最新进展提示了一种新的材料研究范式。然而,原子系统的三维性质以及晶体学材料的周期性和对称性进一步复杂化了常规神经网络对声子态密度的潜在学习,因为这需要昂贵的数据增强来学习三维坐标系统的不同旋转和平移。因此,这些问题突显了获取声子态密度更高效策略的需求。转向ML方法,GNN将原子和它们的键表示为图节点和边,这自然地表示了原子系统。具有增强对称性的GNN [Geiger和Smidt 2022]由于晶体材料的固有对称性而具有优势。然而,在表示和神经网络设计选择方面仍然存在挑战,如实空间和倒空间中性质之间的差异以及输出性质的固定长度(即标量输出)[Delaire等 2009]。这对于具有不同维度程度的材料性质,例如声子能带数的数量,是有问题的[Baroni等 2001]。
7.6.3 现有方法。
在本节中,我们将用于高效准确地预测和分析材料声子性质的方法归为两类:使用局部环境描述符和几何图神经网络。
作为局部环境描述符的一个典型示例,Mortazavi等人[2020]利用机器学习原子间势能(MLIPs)对计算效率高的从头分子动力学轨迹进行训练,提供了一种替代和高效的方法,可用于DFT模拟。在MLIPs中,势能面被描述为与局部环境描述符的函数,这些描述符对于同核原子的旋转、平移和反演是不变的[Behler 2016]。在MLIPs的范畴中,有时刻张量势能(MTPs)[Zuo等人2020],它可以近似任何原子间相互作用[Mortazavi等人2020],因此能够评估与密度泛函摄动理论方法相媲美的声子性质,而不需要大量计算。此外,Ladygin等人[2020]使用MTPs以高精度重现声子性质,与DFT获得的数据相比。利用MTPs的主动学习作为优势,他们在Al、Mo、Ti和U的分子动力学运行上进行了训练。主动学习方法自动调整MTP,仅在数据中存在显著外推时对配置进行训练,从而大大减少了训练MTP所需的DFT计算数量。与DFT和实验数据相比,Al和U的PDOS以及Mo和Ti的声子色散图的MTP和DFT结果之间的误差要小得多。在比较MTP和DFT的振动自由能和熵结果时,也会产生类似的误差。
几何图神经网络从3D原子位置、原子种类和原子间距离中学习材料性质,基于图神经网络。例如,Okabe等人[2023]提出了一种使用虚拟节点图神经网络(VGNN)增强GNNs的方法,该方法可以管理具有可变或甚至是任意维度的输出属性。Okabe等人[2023]提出了三个版本的VGNN,每个版本都采用了对称感知图欧几里得卷积神经网络[Geiger和Smidt 2022]。通过将原子位置和质量表示为周期性图,将输入传递给一系列卷积层,这些卷积层计算输入特征的张量积,然后是非线性层,引入了模型的复杂性。向量虚拟节点(VVN)是最简单的模型,具有m-原子晶体结构输入和3×m Γ-声子能量。矩阵虚拟节点(MVN)对于复杂材料而言更精确,但计算成本更高。最后,动量相关的矩阵虚拟节点(k-MVN)是最复杂的,通过在布里渊区中随机选择k点,可以预测整个声子能带结构。这是通过晶体图中的虚拟动力矩阵(类似于声子动力矩阵)来完成的。然后,材料的训练数据使得可以从优化神经网络来学习矩阵元素。列出的每个模型都不具备原子间力的先验知识,只接受晶体结构作为输入。这种方法提供了一种从复杂材料的晶体结构中获取完整声子能带结构的计算可行策略。Chen等人[2021a]使用三维欧几里得神经网络(𝐸(3)NN)捕获PDOS的主要特征,该网络由𝐸(3)NN开源仓库[Geiger和Smidt 2022]实现。𝐸(3)NN对3D旋转、平移和反演是等变的,因此能够保留所有几何输入以及它们的晶体对称性。数据集是包含1,521个晶体半导体化合物的声子数据库,其中包含基于密度泛函摄动理论[Petretto等人2018]的PDOS数据。𝐸(3)NN成功地复现了实验数据中的关键特征,并直接从原子结构中预测了大量高声子比热容材料,而无需大量计算。
7.6.4 数据集和基准。
据我们所知,尚不存在专门供机器学习方法使用的声子计算标准数据库。然而,从代表性的工作中,这些数据集包括来自Materials Project的约146,000种材料的Γ-声子数据库[Okabe等人2023]和基于DPFT的1,521种半导体化合物的PDOS数据数据库[Petretto等人2018]。然而,机器学习在声子计算中的应用开始要求有一个标准的材料声子数据数据库,以便机器学习方法可以轻松应用。
7.6.5 开放研究方向。
尽管Ladygin等人[2020]的晶格动力学研究主要集中在单组分系统上,但多组分系统也有很有前景的工作。具体来说,M
TP在共价和离子键合系统[Grabowski等人2019]以及金属系统[Novikov和Shapeev 2019]中表现出色。此外,Chen等人[2021a]的欧几里得神经网络工作流突显出一个可以帮助高通量筛选有前景的热材料候选材料的框架,同时还将材料的结构对称性与其声子性质联系起来。