》》》算法竞赛
/*** @file * @author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * @brief 一直在竞赛算法学习的路上* * @copyright 2023.9* @COPYRIGHT 原创技术笔记:转载需获得博主本人同意,且需标明转载源* @language C++* @Version 1.0还在学习中 */
- UpData Log👆 2023.9.26 更新进行中
- Statement0🥇 一起进步
- Statement1💯 有些描述是个人理解,可能不够标准,但能达其意
技术提升站点
文章目录
- 》》》算法竞赛
- 技术提升站点
- 21 树上问题
- 21-0 关于 树 的问题 有哪些?
- 21-1 树的重心
- 21-1-1 重心是什么?
- 21-1-2 重心的性质
- 21-1-2 重心的查找
- 教父(poj 3107)
21 树上问题
树是图的一种特例,树就是 “没有环” 的连通图
判断一个 图 是否是一个 树,需要满足的条件:
-
1)树根:一棵树可以基于
无向图与有向图,区别在于树根。基于无向图的树(无根树),是没有固定树根的(也就是说树根的个数可能不止为1,或说每个结点都能做为树根)
基于有向图的树(有根树),有且仅有一个树根
-
2)父节点与子节点的关系:每个节点有且仅有一个父节点。从根节点遍历,必须由父节点遍历到子节点
-
3)连通性:从 根 出发可以遍历树上所有(除根节点外)节点,且到这些节点的路径只有一条
有根树 与 有向无环图 DAG 的 区别
有向无环图:不能从某点开始经过数点回到该点
有根树 都是 DAG,DAG 不一定是 有根树(如下图:虽然没有构成环,但是4号节点同时拥有两个父节点,不符合有根树的定义)
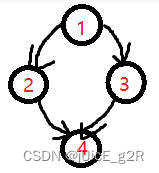
21-0 关于 树 的问题 有哪些?
直通车:
- 树的判断:判定 图 是否为 树 的方法是 DFS遍历
- 树的存储:与 图 的存储方式一致(链式前向星)
- 树的路径问题(包含了 查找最近公共祖先
LCA):点击直通 树的路径问题 - 树的直径
- 树的重心(下文将讲解)
- 多叉树、二叉树
- 树上前缀和,树上差分
21-1 树的重心
21-1-1 重心是什么?
树的重心适用在无根树(一个不含回路的无向图)树的重心是 以任意结点 u 为根 计算它最大子树的节点数 n o d e n node_n noden,如果u节点的 n o d e n node_n noden 最少,则u节点为 树的重心。
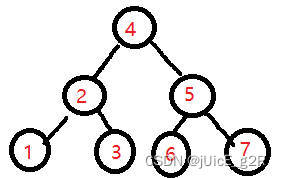
可以一眼看出:4号结点 就是 树的重心,因为这个点能满足 n o d e n node_n noden 是最小的(左子树{4,2,1,3,}:4个,右子树{4,5,6,7}:4个),而其他任意一个节点的子树(例如 2号节点的最大子树{2,4,5,6,7}5个)都是比这个点的最大子树的节点数是大的。
21-1-2 重心的性质
- 以树的重心为根时,所有子树的大小都不超过整棵树大小的一半。(树上分治会用到)
- 树的重心如果不唯一,则至多有两个,且这两个重心相邻。

- 树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。
- 把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。

- 在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。(往树上增加或减少一个叶子,如果原节点数是奇数,那么重心可能增加一个,原重心仍是重心;如果原节点数是偶数,重心可能减少一个,另一个重心仍是重心)
21-1-2 重心的查找
教父(poj 3107)
问题描述
城里有一个黑手党组织。把黑手党的人员关系用一棵树来描述,教父是树的根,每个节点是一个组织成员。为了保密,每人只和他的父节点和他的子节点联系。警察知道哪些人互相来往,但是不知他们的关系。警察想找出谁是教父。
警察假设教父是一个聪明人:教父懂得制衡手下的权力,所以他直属的几个小头目,每个人的属下的人数差不多。也就是说,删除根之后,剩下几棵互不连通的子树(连通块),其中最大的连通块应该尽可能小。请帮助警察找到哪些人可能是教父。
输入:第1行输入n,表示组织人数, 2 ≤ n ≤ 50000 2\leq n \leq 50000 2≤n≤50000 。组织成员的编号为1~n。下面n-1行中,每行输入两个整数,即有联系的两个人的编号。
输出:输出疑似教父的节点编号,从小到大输出。Input
6 1 2 2 3 2 5 3 4 3 6Output
2 3
- 分析
“删除根之后,剩下几棵互不连通的子树(连通块),其中最大的连通块应该尽可能小”,这句话说明了 教父 就是 这个关系树里的 重心
如何计算以 u节点 为根的子树的结点
u节点 DFS 直到“碰壁”后,将栈里的数据依次弹出,弹出一个结点数加1。
那么这样的话,可以对删除根之后,剩下几棵互不连通的子树(连通块) 进行单独的DFS,对整棵树逐一删除节点,重复上述步骤,就能得到每个结点的最大连同块。
如何优化?
上面提出的方案是 使用 暴力法 解决,其实无需如此,可以依照线段树的思维,对 同父节点的子节点 进行合并,得到父节点的子树的节点数,这样一次DFS就可以解决问题。
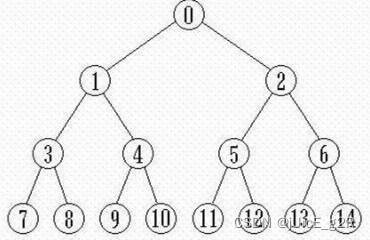
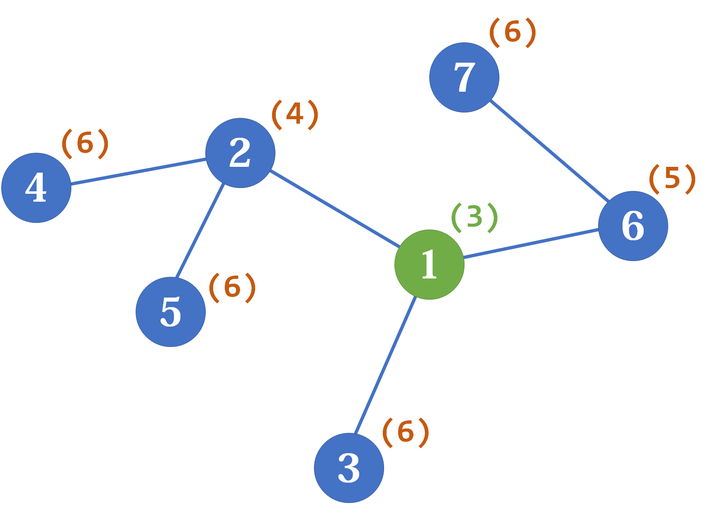
如上图,假如删除 结点1,得到3个连通块(含结点1的邻居:节点3、含结点1的邻居:节点0、含结点1的邻居:节点4)
对任意点做一次 DFS,特殊点,以 结点2为根节点 做DFS:
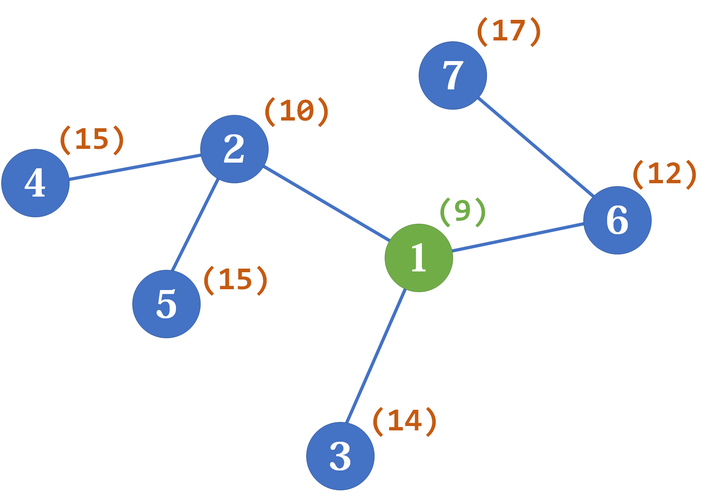
从2向0方向 一直DFS,直到遍历到节点10,停止遍历,栈开始弹出数据。,当弹出结点10时,记录 结点10 的度(即子树的结点数) D e g r e e [ 10 ] = 1 Degree[10]=1 Degree[10]=1,同理 D e g r e e [ 9 ] = 1 Degree[9]=1 Degree[9]=1;当弹出4时, D e g r e e [ 4 ] = D e g r e e [ 9 ] + D e g r e e [ 10 ] + 1 = 3 Degree[4]=Degree[9]+Degree[10]+1=3 Degree[4]=Degree[9]+Degree[10]+1=3,同理算出 D e g r e e [ 3 ] = D e g r e e [ 7 ] + D e g r e e [ 8 ] + 1 = 3 Degree[3]=Degree[7]+Degree[8]+1=3 Degree[3]=Degree[7]+Degree[8]+1=3;在弹出1时, D e g r e e [ 1 ] = D e g r e e [ 3 ] + D e g r e e [ 4 ] + 1 = 7 Degree[1]=Degree[3]+Degree[4]+1=7 Degree[1]=Degree[3]+Degree[4]+1=7;删除1后, D e g r e e [ 0 ] = n − D e g r e e [ 1 ] Degree[0]=n-Degree[1] Degree[0]=n−Degree[1]
存储:链式前向星
链式前向星较领接矩阵(二维数组)在空间上优化了很多
点击直通 链式前向星(图(树)的存储)
- 代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
vector<int> head(N,-1);
struct Edge{int to,next;Edge():to(-1), next(-1){} //初始化为无邻居节点
} edge[N<<1];
vector<int> Degree(N,1); //初始化每个节点的度(子树的结点数)为1
int edge_n=0; //记录边数
int GodFather_n=0; //记录可能得教父个数
int n; //人有n个,关系有n-1条
int MAX_Degree=1e9;
vector<int> ans(N,0);
void Add_Edge(int u, int v){edge[edge_n].to=v;edge[edge_n].next=head[u]; //记录 上一个邻居节点 的 存储编号head[u]=edge_n++; //当前 邻居节点 的 存储编号,以便下一个邻居节点的访问
}
void DFS(int u=1, int father=0){/*计算 cur结点 的 最大连通块的结点数*/int temp=0;for(int i=head[u]; ~i; i=edge[i].next){ //遍历cur节点的邻居节点[~i相当于i=-1]int v=edge[i].to; //v 是 u 的子节点if(v==father) continue;DFS(v,u); //DFS子树Degree[u]+=Degree[v]; //更新父节点的度temp=max(temp, Degree[v]); //记录cur结点的 最大子树 的 结点数}temp=max(temp, n-Degree[u]); //temp是cur最大连通块的节点数/*查找 结点数 最小的 最大连通块*/if(temp<MAX_Degree){ //满足条件的话,则temp是 疑似教父 的最大连通块的结点数MAX_Degree=temp; //更新 最小的 最大连通块GodFather_n=0; //找到新的最小,将它放在第一个ans[++GodFather_n]=u;}else if(temp==MAX_Degree)ans[++GodFather_n]=u;
}int main(int* argc, void* argv[]){cin>>n;for(int i=1; i<n;i++){int u,v; cin>> u >> v;Add_Edge(u,v); Add_Edge(v,u); //无向 记录 双向有向}DFS();sort(ans.data()+1, ans.data()+1+GodFather_n); //升序排列for(int i=1; i<=GodFather_n; i++)cout<<ans[i]<<" ";return 0;
}