目录

第一题

题目来源

题目内容

解决方法

方法一：回溯算法

方法二：permute方法

方法三：交换法

第二题

题目来源

题目内容

解决方法

方法一：回溯算法

方法二：递归和交换

方法三：二维列表

第三题

题目来源

题目内容

解决方法

方法一：旋转90度

方法二：使用辅助数组

方法三：先转置后反转

方法四：坐标变换

---

第一题

题目来源

46. 全排列 - 力扣（LeetCode）

题目内容

解决方法

方法一：回溯算法

这道题可以使用回溯算法来解决。具体思路如下：

1、创建一个结果集列表 result 来存储所有可能的全排列。
2、创建一个临时列表 tempList 来存储当前正在生成的排列。
3、创建一个布尔数组 used，用于标记数字是否已经被使用过。
4、调用回溯函数 backtrack，传入初始参数：nums 数组、used 数组、tempList 列表和 result 结果集。
5、在回溯函数中，首先判断当前排列的长度是否等于 nums 数组的长度，如果是，则说明已经完成了一种排列，将其加入结果集 result 中。
6、否则，遍历 nums 数组中的每个数字：

• 如果该数字已经被使用过（即 used[i] 为 true），则跳过该数字，继续下一个循环。
• 如果该数字未被使用过，则将其添加到 tempList 中，并将 used[i] 设置为 true，表示该数字已经被使用。
• 然后进行下一层递归，即调用 backtrack 函数。
• 在递归返回后，需要进行回溯操作，即将刚才添加的数字从 tempList 中移除，并将 used[i] 设置为 false，表示该数字未被使用。

7、回溯函数返回后，所有的排列都已经生成完毕，将结果集 result 返回。
这样，通过回溯的递归过程，可以生成所有可能的全排列。

import java.util.ArrayList;
import java.util.List;class Solution {public List<List<Integer>> permute(int[] nums) {List<List<Integer>> result = new ArrayList<>();List<Integer> tempList = new ArrayList<>();boolean[] used = new boolean[nums.length];backtrack(nums, used, tempList, result);return result;}private void backtrack(int[] nums, boolean[] used, List<Integer> tempList, List<List<Integer>> result) {if (tempList.size() == nums.length) {result.add(new ArrayList<>(tempList));return;}for (int i = 0; i < nums.length; i++) {if (used[i]) continue; // 如果该数已经被使用过，则跳过tempList.add(nums[i]);used[i] = true;backtrack(nums, used, tempList, result);tempList.remove(tempList.size() - 1);used[i] = false;}}
}

复杂度分析：

• 时间复杂度： 在回溯算法中，我们需要生成所有可能的全排列。对于每个位置，我们有N种选择。因此，在最坏的情况下，需要进行N次选择操作。对于每个选择，递归地搜索剩下的位置。因此，总的时间复杂度为O(N!)，其中N是nums数组的长度。
• 空间复杂度： 在回溯算法中，我们使用了一个临时列表 tempList 和一个布尔数组 used。在每一层递归调用时，tempList 的长度最多为N，used 数组也会占用N个空间。递归调用栈的深度最大为N。因此，总的空间复杂度为O(N)。

综上所述，该解法的时间复杂度为O(N!)，空间复杂度为O(N)。

LeetCode运行结果：

方法二：permute方法

除了回溯算法外，还可以使用Java的库函数Collections中的permute方法来生成全排列。具体步骤如下：

• 将给定的数组转换为List类型。
• 使用Collections类中的permute方法生成所有可能的全排列。
• 将结果转换为List<List<Integer>>类型的形式。

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;class Solution {public List<List<Integer>> permute(int[] nums) {List<List<Integer>> result = new ArrayList<>();// 转换为List类型List<Integer> list = new ArrayList<>();for (int num : nums) {list.add(num);}// 使用库函数生成全排列permuteHelper(list, 0, result);return result;}private void permuteHelper(List<Integer> list, int start, List<List<Integer>> result) {if (start == list.size()) {result.add(new ArrayList<>(list));} else {for (int i = start; i < list.size(); i++) {// 交换元素Collections.swap(list, start, i);// 继续生成后面的排列permuteHelper(list, start + 1, result);// 恢复原始顺序Collections.swap(list, start, i);}}}
}

复杂度分析：

• 时间复杂度：在这种解法中，我们使用了Collections.permute函数来生成全排列。该函数的时间复杂度是O(N!)，其中N是数组的长度。
• 空间复杂度：在这个解法中，我们创建了一个二维列表 result 来存储所有可能的全排列。这个二维列表的空间复杂度是O(N!)，其中N是数组的长度。同时，也需要考虑到递归调用栈的空间消耗，因为在permuteHelper函数中进行了递归调用。递归调用的深度最大为N，所以递归调用栈的空间复杂度也是O(N)。

综上所述，使用库函数Collections.permute的解法的时间复杂度为O(N!)，空间复杂度为O(N!)。

LeetCode运行结果：

方法三：交换法

除了回溯算法和库函数Collections，还可以使用交换法来生成全排列。

交换法的思路是：

1. 从数组的第一个位置开始，依次将每个位置的元素与后面的元素交换，得到不同的排列。
2. 对于每个位置，将其与后面的元素进行交换，然后递归地处理剩下的位置。
3. 当处理到最后一个位置时，将当前排列加入结果中。

import java.util.ArrayList;
import java.util.List;class Solution {public List<List<Integer>> permute(int[] nums) {List<List<Integer>> result = new ArrayList<>();// 转换为List类型List<Integer> list = new ArrayList<>();for (int num : nums) {list.add(num);}permuteHelper(list, 0, result);return result;}private void permuteHelper(List<Integer> list, int start, List<List<Integer>> result) {if (start == list.size() - 1) {result.add(new ArrayList<>(list));} else {for (int i = start; i < list.size(); i++) {Collections.swap(list, start, i); // 交换元素permuteHelper(list, start + 1, result); // 递归处理下一个位置Collections.swap(list, start, i); // 恢复原始顺序}}}
}

复杂度分析：

• 时间复杂度：在这种解法中，我们使用了递归来生成全排列。每次递归都会将当前位置的元素与后面的元素进行交换，所以总共需要进行N次交换操作。对于每次交换操作，有N-1个选择，因此总的时间复杂度为O(N * N!)。
• 空间复杂度：在这个解法中，我们创建了一个二维列表 result 来存储所有可能的全排列。这个二维列表的空间复杂度是O(N!)，其中N是数组的长度。同时，也需要考虑到递归调用栈的空间消耗，因为在permuteHelper函数中进行了递归调用。递归调用的深度最大为N，所以递归调用栈的空间复杂度也是O(N)。

综上所述，使用交换法的解法的时间复杂度为O(N * N!)，空间复杂度为O(N!)。

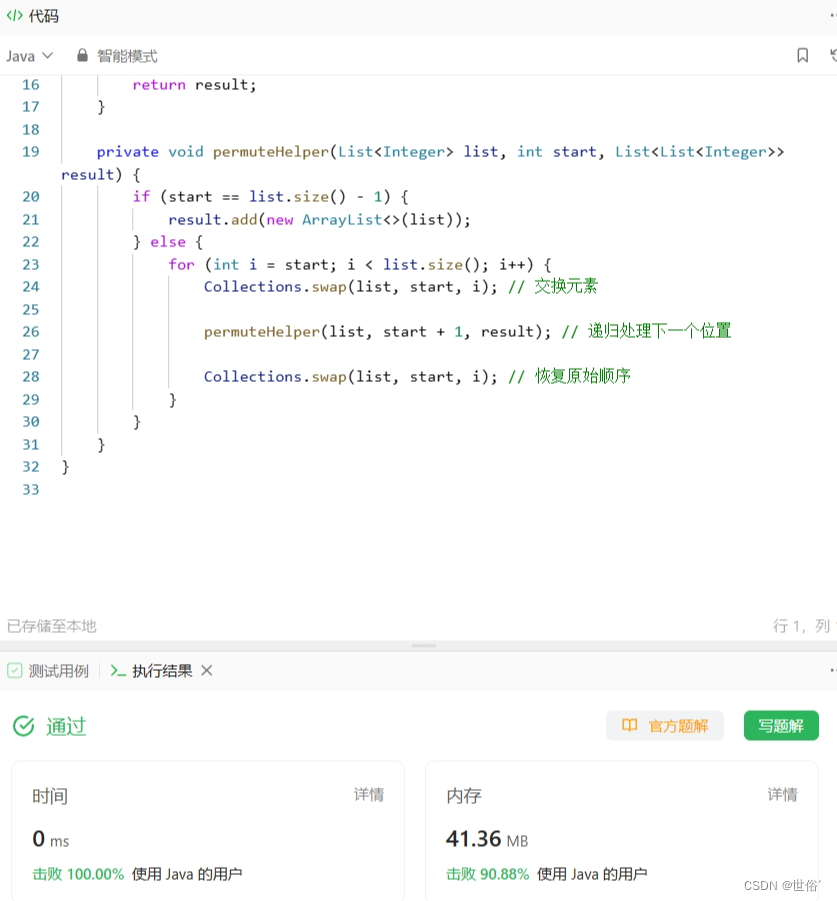
LeetCode运行结果：

第二题

题目来源

47. 全排列 II - 力扣（LeetCode）

题目内容

解决方法

方法一：回溯算法

可以使用回溯算法来解决这个问题。回溯算法通过遍历所有可能的解空间来找到问题的解。

具体步骤如下：

1. 首先将给定的序列 nums 进行排序，以便于后续处理。

2. 创建一个空列表 result 来存储所有的全排列。

3. 创建一个空列表 path 来存储当前正在构建的排列。

4. 创建一个与 nums 长度相等的布尔数组 used，用于记录每个元素是否已经被使用过。

5. 调用回溯函数 backtrack(0) 开始生成全排列。

6. 在回溯函数 backtrack 中，首先判断如果 path 的长度等于 nums 的长度，则将 path 加入到 result 中，并返回。

7. 否则，遍历 nums 数组，对于每个元素 nums[i]，进行以下操作：

   • 如果当前元素 nums[i] 已经被使用过（used[i] = true），则跳过该元素。

   • 如果当前元素 nums[i] 与前一个元素相同，并且前一个元素还没有被使用过（used[i-1] = false），则跳过该元素。这是为了避免生成重复的排列。

   • 将当前元素 nums[i] 添加到 path 中，并将 used[i] 设置为 true，表示已经使用过。

   • 递归调用 backtrack(i+1) 继续生成下一个位置的元素。

   • 回溯：将当前元素从 path 中移除，并将 used[i] 设置为 false，表示回溯到上一层。

8. 最后返回 result。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;public class Solution {public List<List<Integer>> permuteUnique(int[] nums) {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();boolean[] used = new boolean[nums.length];Arrays.sort(nums); // 对nums进行排序backtrack(nums, used, path, result);return result;}private void backtrack(int[] nums, boolean[] used, List<Integer> path, List<List<Integer>> result) {if (path.size() == nums.length) {result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if (used[i]) {continue;}if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue;}path.add(nums[i]);used[i] = true;backtrack(nums, used, path, result);path.remove(path.size() - 1);used[i] = false;}}
}

复杂度分析：

对于给定长度为 n 的序列 nums，我们来分析一下算法的时间复杂度和空间复杂度。

时间复杂度：

• 排序 nums 数组的时间复杂度为 O(nlogn)。
• 回溯算法的时间复杂度为 O(n!)，其中 n! 表示全排列的个数。在最坏情况下，所有元素都不相同，共有 n! 个全排列。
• 综上所述，算法的总时间复杂度为 O(nlogn + n!)。

空间复杂度：

• 算法使用了额外的空间来存储结果集和回溯过程中的临时路径，即列表 result 和 path，它们的空间复杂度为 O(n!)。
• used 数组的空间复杂度为 O(n)，用于记录每个元素是否已经被使用过。
• 综上所述，算法的总空间复杂度为 O(n!)。

需要注意的是，由于全排列的个数可以很大（n!），因此在实际应用中，当 n 较大时，算法可能会耗费较多的时间和空间资源。

LeetCode运行结果：

方法二：递归和交换

除了回溯算法，我们还可以使用其他方法来解决这个问题。

一种常用的方法是使用递归和交换元素的方式来生成全排列。具体步骤如下：

1. 首先创建一个空列表 result 来存储所有的全排列。

2. 调用递归函数 backtrack(nums, 0, result) 开始生成全排列。

3. 在递归函数 backtrack 中，首先判断如果当前位置 index 等于 nums 数组的长度，则将当前排列加入到 result 中，并返回。

4. 否则，遍历从 index 到 nums 数组末尾的所有位置，对于每个位置 i，进行以下操作：

   • 如果当前位置 index 和位置 i 的元素相同，则跳过该位置，以避免生成重复的排列。

   • 将当前位置 index 和位置 i 的元素交换。

   • 递归调用 backtrack(nums, index + 1, result) 继续生成下一个位置的元素。

   • 回溯：将当前位置 index 和位置 i 的元素交换回来。

5. 最后返回 result。

import java.util.ArrayList;
import java.util.List;public class Solution {public List<List<Integer>> permuteUnique(int[] nums) {List<List<Integer>> result = new ArrayList<>();backtrack(nums, 0, result);return result;}private void backtrack(int[] nums, int index, List<List<Integer>> result) {if (index == nums.length) {List<Integer> permutation = new ArrayList<>();for (int num : nums) {permutation.add(num);}result.add(permutation);return;}for (int i = index; i < nums.length; i++) {if (isDuplicate(nums, index, i)) {continue;}swap(nums, index, i);backtrack(nums, index + 1, result);swap(nums, index, i); // 回溯}}private boolean isDuplicate(int[] nums, int start, int end) {for (int i = start; i < end; i++) {if (nums[i] == nums[end]) {return true;}}return false;}private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}

这样就可以通过调用 permuteUnique 方法来获取给定序列的所有不重复全排列。这种方法在实现上更加简洁，但是在效率上可能略逊于回溯算法。 

复杂度分析：

时间复杂度：

• 在递归函数中，对每个位置都进行了不重复全排列的探索，时间复杂度为 O(n!)，其中 n 表示数组 nums 的长度。
• 对于每个位置，需要遍历从当前位置到数组末尾的所有元素，时间复杂度为 O(n)，其中 n 表示数组 nums 的长度。
• 综上所述，算法的总时间复杂度为 O(n * n!)。

空间复杂度：

• 使用了额外的空间来存储结果集和递归过程中的临时路径，即列表 result 和递归调用栈的开销。
• 结果集 result 最多包含 n! 个全排列，因此空间复杂度为 O(n!)。
• 递归调用栈的最大深度为 n，因此空间复杂度为 O(n)。
• 综上所述，算法的总空间复杂度为 O(n + n!)。

需要注意的是，全排列的个数可以很大（n!），因此在实际应用中，当 n 较大时，算法可能会耗费较多的时间和空间资源。

LeetCode运行结果：

方法三：二维列表

除了回溯算法和递归交换元素，我们还可以使用其他方法来生成全排列。以下是另一种常用的方法：

1. 首先，将数组 nums 转换为一个 ArrayList 来方便后续操作。

2. 创建一个空的二维列表 result 来存储全排列。

3. 调用递归函数 permuteUniqueHelper(ArrayList<Integer> nums, int start, List<List<Integer>> result) 来生成全排列。

4. 在递归函数 permuteUniqueHelper 中，首先判断如果当前位置 start 等于 nums 列表的长度，则将当前排列加入到 result 中，并返回。

5. 否则，遍历从 start 到 nums 列表末尾的所有位置，对于每个位置 i，进行以下操作：

   • 如果当前位置 start 和位置 i 的元素相同，则跳过该位置，以避免生成重复的排列。

   • 交换当前位置 start 和位置 i 的元素。

   • 将当前位置 start 的元素固定，继续递归调用 permuteUniqueHelper(nums, start + 1, result) 来生成下一个位置的元素。

   • 回溯：恢复位置 start 和位置 i 的元素的原始顺序。

6. 最后返回 result。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;public class Solution {public List<List<Integer>> permuteUnique(int[] nums) {List<List<Integer>> result = new ArrayList<>();ArrayList<Integer> numsList = new ArrayList<>();for (int num : nums) {numsList.add(num);}permuteUniqueHelper(numsList, 0, result);return result;}private void permuteUniqueHelper(ArrayList<Integer> nums, int start, List<List<Integer>> result) {if (start == nums.size()) {result.add(new ArrayList<>(nums));return;}for (int i = start; i < nums.size(); i++) {if (isDuplicate(nums, start, i)) {continue;}// 交换位置 start 和位置 i 的元素swap(nums, start, i);// 固定位置 start 的元素，递归生成下一个位置的元素permuteUniqueHelper(nums, start + 1, result);// 恢复位置 start 和位置 i 的元素的原始顺序，进行回溯swap(nums, start, i);}}private boolean isDuplicate(ArrayList<Integer> nums, int start, int end) {for (int i = start; i < end; i++) {if (nums.get(i).equals(nums.get(end))) {return true;}}return false;}private void swap(ArrayList<Integer> nums, int i, int j) {Integer temp = nums.get(i);nums.set(i, nums.get(j));nums.set(j, temp);}
}

这种方法与之前的方法相比稍微简洁一些，并且在效率上也具有一定优势。同样地，需要注意全排列的个数可能很大，因此在处理较大规模的输入时仍然需要谨慎考虑算法的时间和空间复杂度。 

复杂度分析：

时间复杂度：

• 对于每个位置，我们需要遍历从该位置到数组末尾的所有元素，所以在递归函数中，我们有一个循环，其迭代次数是 n - start，其中 n 是数组的长度。
• 在每个位置上，我们需要判断当前元素是否与之前固定的元素重复，这涉及到遍历之前的元素集合。因此，在每个位置上，我们还有一个内层循环，其迭代次数不会超过当前位置的索引。
• 综上所述，在递归函数中，总的时间复杂度为 O(n!)。这是因为对于每个排列，我们需要进行 n 次交换操作，所以时间复杂度是阶乘级别的。

空间复杂度：

• 我们使用了一个二维列表 result 来存储所有的全排列结果，所以需要额外的空间来存储这些结果。这些结果的数量是 n!，所以空间复杂度是 O(n!)。
• 另外，我们使用了一个 ArrayList numsList 来将传入的数组转换为列表，所以需要额外的 O(n) 的空间来存储该列表。

综上所述，该方法的时间复杂度是 O(n!)，空间复杂度是 O(n!)，其中 n 是数组的长度。需要注意的是，由于全排列的数量是非常大的，因此在处理较大规模的输入时，可能会受到时间和空间复杂度的限制。

LeetCode运行结果：

第三题

题目来源

48. 旋转图像 - 力扣（LeetCode）

题目内容

解决方法

方法一：旋转90度

题目要求将给定的二维矩阵顺时针旋转90度，并且需要在原地修改输入的矩阵。

解题思路：

1. 首先，将矩阵沿副对角线翻转。可以通过使用两个循环，分别遍历矩阵的上半部分，交换对应位置的元素，实现翻转。
2. 然后，将矩阵沿水平中线翻转。同样使用两个循环，分别遍历矩阵的上半部分和下半部分，交换对应位置的元素，实现翻转。

通过以上步骤，就可以将矩阵顺时针旋转90度。注意，这里的翻转操作是在原矩阵上进行的，因此不需要使用额外的空间。

class Solution {
public void rotate(int[][] matrix) {int n = matrix.length;// 先将矩阵沿副对角线翻转for (int i = 0; i < n; i++) {for (int j = 0; j < n - i; j++) {int temp = matrix[i][j];matrix[i][j] = matrix[n - j - 1][n - i - 1];matrix[n - j - 1][n - i - 1] = temp;}}// 再将矩阵沿水平中线翻转for (int i = 0; i < n / 2; i++) {for (int j = 0; j < n; j++) {int temp = matrix[i][j];matrix[i][j] = matrix[n - i - 1][j];matrix[n - i - 1][j] = temp;}}
}}

复杂度分析：

对于给定的 n × n 矩阵，我们需要沿副对角线翻转矩阵并沿水平中线翻转矩阵，来完成顺时针旋转90度的操作。

时间复杂度分析：

• 沿副对角线翻转的过程，需要遍历矩阵的上半部分元素，共有 n(n+1)/2 个元素。因此，时间复杂度为 O(n^2)。
• 沿水平中线翻转的过程，需要遍历矩阵的上半部分和下半部分元素，共有 n(n/2) 个元素。因此，时间复杂度同样为 O(n^2)。 总体时间复杂度为 O(n^2)。

空间复杂度分析：

• 原地修改输入的矩阵，不需要使用额外的空间。因此，空间复杂度为 O(1)。

综上所述，该算法的时间复杂度为 O(n^2)，空间复杂度为 O(1)。

LeetCode运行结果：

方法二：使用辅助数组

该方法通过创建一个辅助数组来存储旋转后的矩阵元素，然后将辅助数组中的元素重新赋值给原矩阵。

class Solution {
public void rotate(int[][] matrix) {int n = matrix.length;int[][] temp = new int[n][n];// 将矩阵元素赋值给辅助数组for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {temp[i][j] = matrix[i][j];}}// 将辅助数组中的元素按规则赋值给原矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {matrix[j][n - i - 1] = temp[i][j];}}
}}

复杂度分析：

时间复杂度分析：

• 创建辅助数组需要遍历原矩阵的所有元素，时间复杂度为 O(n^2)。
• 将辅助数组的元素重新赋值给原矩阵也需要遍历所有元素，时间复杂度为 O(n^2)。 总体时间复杂度为 O(n^2)。

空间复杂度分析：

• 需要创建一个与原矩阵大小相同的辅助数组，因此空间复杂度为 O(n^2)。

LeetCode运行结果：

方法三：先转置后反转

该方法先将矩阵进行转置操作（行列互换），然后再对每一行进行反转操作。

class Solution {
public void rotate(int[][] matrix) {int n = matrix.length;// 转置矩阵for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// 反转每一行for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {int temp = matrix[i][j];matrix[i][j] = matrix[i][n - j - 1];matrix[i][n - j - 1] = temp;}}
}}

复杂度分析：

时间复杂度分析：

• 转置矩阵的过程需要遍历矩阵中的上三角部分元素，共有 n(n+1)/2 个元素，因此时间复杂度为 O(n^2)。
• 反转每一行的过程需要遍历矩阵中的每一行的前一半元素，共有 n(n/2) 个元素，因此时间复杂度同样为 O(n^2)。 总体时间复杂度为 O(n^2)。

空间复杂度分析：

• 原地修改输入的矩阵，不需要使用额外的空间。因此，空间复杂度为 O(1)。

LeetCode运行结果：

方法四：坐标变换

还有一种基于坐标变换的方法可以实现矩阵的旋转。

该方法的思想是通过找到旋转前后对应位置的关系，直接将旋转后的元素赋值给旋转前的位置。这种方法通过循环遍历矩阵中的四个角落的元素，逐步交换它们的值，实现矩阵的旋转。

class Solution {
public void rotate(int[][] matrix) {int n = matrix.length;// 对每个元素进行旋转for (int i = 0; i < n / 2; i++) {for (int j = i; j < n - i - 1; j++) {int temp = matrix[i][j];matrix[i][j] = matrix[n - j - 1][i];matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];matrix[j][n - i - 1] = temp;}}
}}

复杂度分析：

时间复杂度分析：

• 循环嵌套的两个 for 循环遍历了矩阵的四分之一，因此时间复杂度为 O(n^2/4)，即 O(n^2)。
• 在每个内部循环中，交换四个元素的值需要常数时间。 总体时间复杂度为 O(n^2)。

空间复杂度分析：

• 该方法在原矩阵上进行操作，不需要额外的辅助数组，因此空间复杂度为 O(1)。

综上所述，该方法的时间复杂度为 O(n^2)，空间复杂度为 O(1)。这是一种高效的解决方案。

LeetCode运行结果：