机器学习——一元线性回归构造直线，并给出损失函数

Question

在二维平面有n个点，如何画一条直线，使得所有点到该直线距离之和最短

如果能找到，请给出其损失函数

问题分析

1.概念补充

关于损失函数：

也即代价函数，是一个量化误差的表达式

参考链接：线性回归与非线性回归：1.0一元线性回归与代价函数（损失函数）_在一元线性回归中,哪个函数不适用于损失函数(-CSDN博客

本文中我们采用`观测值与实际值差的平方`作为损失函数

具体原理参考链接：知乎形象举例——梯度下降算法

下面是MSE函数，但是我这里就没有除以2了，所以偏导应当有一个2倍

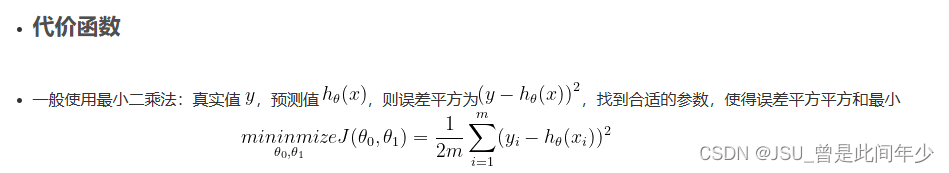
2.流程分析

对于此问题，我们应当按如下步骤进行求解

首先，我们需要对于指定初始的k与b初始化该直线

然后，对学习率（也即步长）和迭代次数进行适当调整

最后，在得到满意的结果后终止调整，整理结果，给出最终参数

3.注意

我们用的并不是直线距离进行损失计算，而是用的△y进行计算，

但是结果并没有影响，因为经过推倒后，距离d与△y成正比

具体实现

本文参考多方资料，使用python代码手写一元线性回归进行求解

计算当前参数下的最小二乘法结果：

def calcLoseFunction(k,b,XData,YData):sum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum

梯度下降法进行搜索：

#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和sumk += -(1 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(1 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b

最终成果

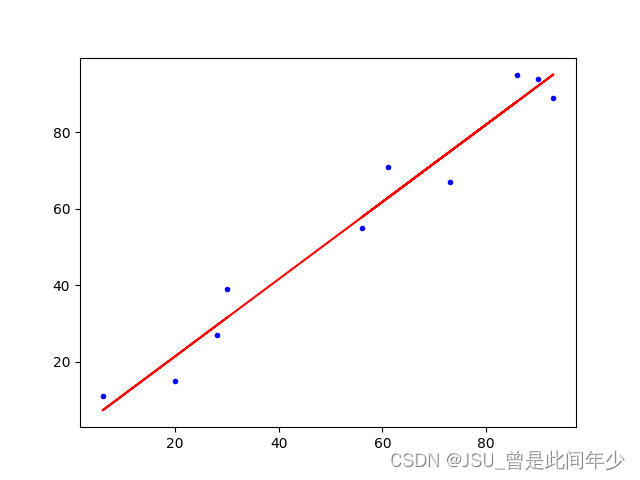
采用随机来对点进行生成，大部分测试较为稳定，模型较为拟合

但是由于X,Y都进行随机生成，按照期望来说，在100*100的矩阵范围内数据呈现均匀分布

于是改造Y数据生成方式为：

YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]

调整初始斜率k=0.5进行测试，最终结果较为拟合，效果较好

代码

import numpy #发现直接用List就行了
import random
import matplotlib.pyplot as plt
# random.random()
# random.randint(start,stop)
#################全局数据定义区
# 数组大小
listSize=10
# 定义学习率 取尽量小0.001
learningRate=0.0001
#定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k,b=0.5,1
#定义迭代次数
bfsNums=9999
#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):# [1-100]return random.randint(start, end)# 打印本次随机生成的X,Y 便于快速粘贴复现
def printXYArray(XData,YData):# 打印Xprint("[", ",".join([str(i) for i in XData]), "]")# 打印Yprint("[", ",".join([str(i) for i in YData]), "]")# 最小二乘法定义损失函数 并计算
#参考链接：https://blog.csdn.net/zy_505775013/article/details/88683460
# 求最小二乘法的最小值 最终结果应当是在learningRate一定情况下  这个最小的sum
def calcLoseFunction(k,b,XData,YData):sum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和  注意这里求偏导应当是两倍 不知道为什么写成1了# 求MSE的偏导sumk += -(2 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(2 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b# 随机生成横坐标
XData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 随机生成纵坐标
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
# XData=testArrayX
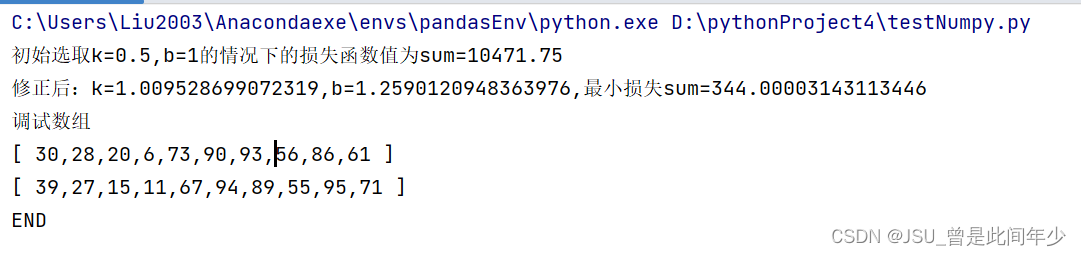
# YData=testArrayYprint("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k,b,calcLoseFunction(k,b,XData,YData)))
# 对k,b进行梯度修正
k,b=calcGradientCorrection(b,k,XData,YData,learningRate,bfsNums)
print("修正后：k={},b={},最小损失sum={}".format(k,b,calcLoseFunction(k,b, XData, YData)))
print("调试数组")
printXYArray(XData,YData)#画图
plt.plot(XData, YData, 'b.')
plt.plot(XData, k*numpy.array(XData)+b, 'r')
plt.show()
print("END")