C++ AB组辅导课
- 蓝桥杯C++ AB组辅导课 第一讲 递归与递推 Acwing
- 1、整数划分(递归)
- 2、acwing92. 递归实现指数型枚举
- 10凑算式(全排列)
- 11李白打酒(全排列)
- 12、棋牌总数(递归)
- 13、剪邮票(递归)
- 14、1050. 鸣人的影分身 (递归或动态规划(记忆化搜索))
- 15、方格分割 (dfs+思维)
- 蓝桥杯C++ AB组辅导课 第三讲 数学与简单DP
- 4、包子凑数
- 5、测试次数(最优解问题——>dp)
- 数论
- 3、acwing2058. 笨拙的手指(进制转换)
- 4、AcWing 1346. 回文平方(回文判断、进制转换)
- 6、AcWing 428. 数列(二进制,映射)
- 7、1431分糖果
- 蓝桥杯C++ AB组辅导课 第四讲 枚举、模拟与排序 Acwing
- 1、AcWing 1210.连号区间数(枚举)
- 5、AcWing466.回文日期(回文,日期,模拟)
- 7、AcWing1229.日期问题(字符串+时间格式)
- 图论
- 1、acwing2019. 拖拉机(最短路径+双向队列)
- 往年题目汇总
- 2015-2018
- 2013年
- 2018年
- 2019年
- 2020年
- 2021年
- (8)、其他进制转化为十进制
- 十进制转化成其他进制:短除法
- 其他进制转化成十进制:秦九韶算法
蓝桥杯C++ AB组辅导课 第一讲 递归与递推 Acwing
1、整数划分(递归)
算法设计与分析——分治与递归——整数划分问题
#include<bits/stdc++.h>
using namespace std;int n;int dfs(int a, int b)
{if((a<0)||(b<0))return 0;if((a==1)||(b==1))return 1;if(a<b)return dfs(a,a);if(a==b)return (1+dfs(a,b-1)); //划分 包含 b, 不包含 b if(1<b<a)return dfs(a-b,b)+dfs(a,b-1);//划分里 包含b 不包含b
}int main()
{cin>>n;cout<<dfs(n,n)<<endl; return 0;}
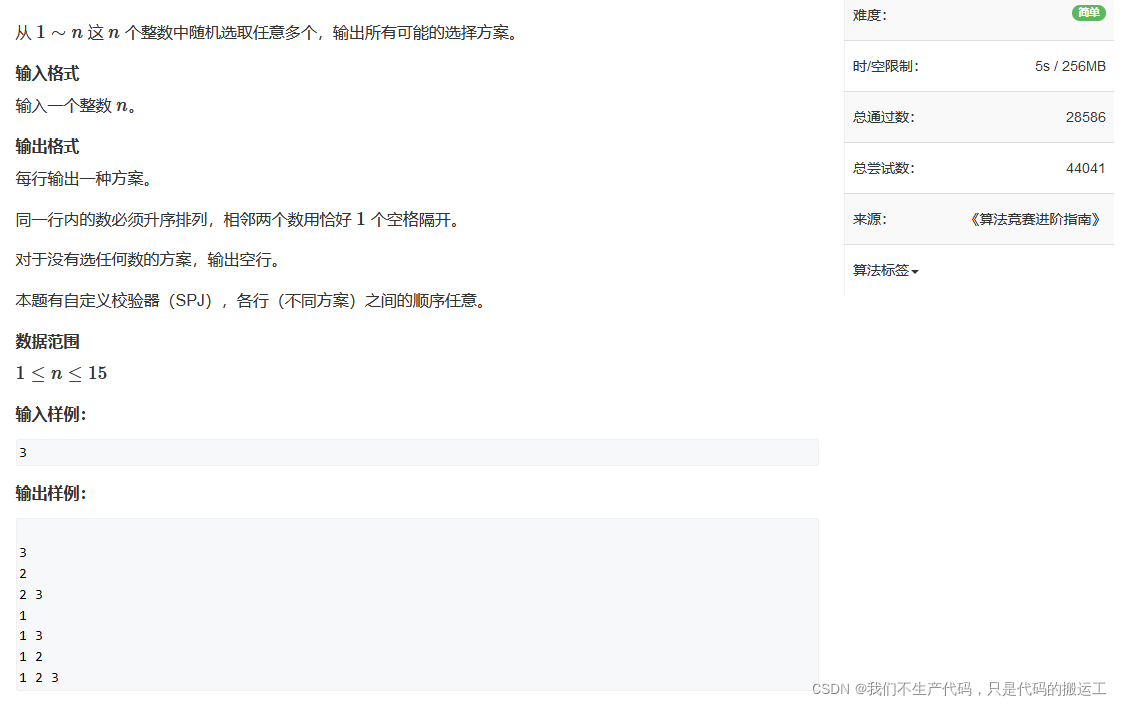
2、acwing92. 递归实现指数型枚举
acwing92. 递归实现指数型枚举
#include <iostream>
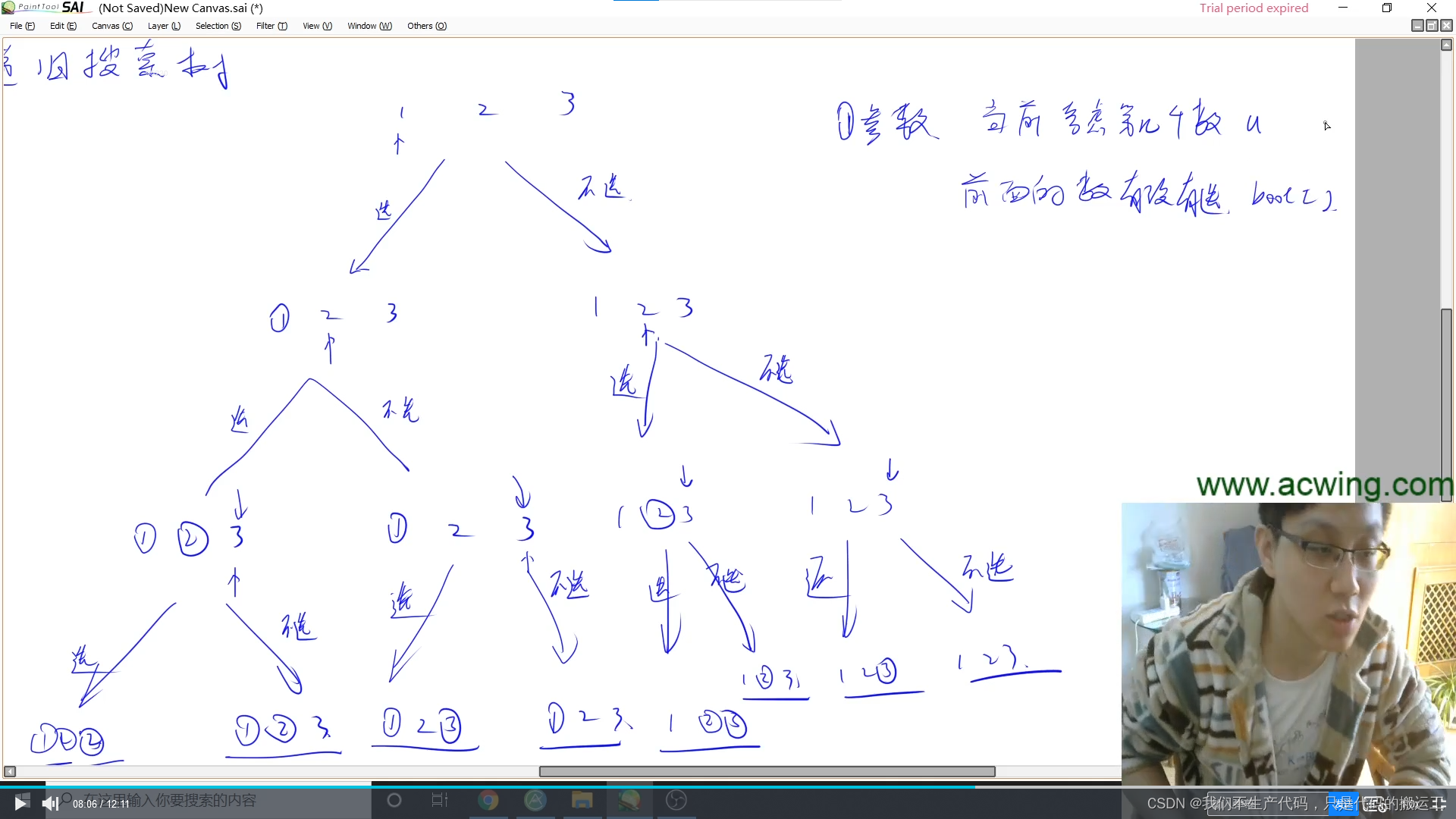
using namespace std;const int N=20;int n;bool vis[N]; //判断选还是不选void DFS(int u) //第几层就是筛选第几个数字
{if(u>n) //不可以有等号,如果有等号会少一层递归,即最后一层无法递归 {for(int i=1;i<=n;i++)//从1到n选择if(vis[i]) //把选择的数打印出来cout<<i<<" ";cout<<endl;return ;}else {vis[u]=true;//选这个数字DFS(u+1);vis[u]=false;//不选这个数字DFS(u+1);}
}
int main() {cin>>n;DFS(1); //从1开始选择,到n结束,所以不能从0开始;return 0;
}10凑算式(全排列)
凑算式B DEF
A + --- + ------- = 10C GHI(如果显示有问题,可以参见【图1.jpg】)这个算式中A~I代表1~9的数字,不同的字母代表不同的数字。比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。这个算式一共有多少种解法?注意:你提交应该是个整数,不要填写任何多余的内容或说明性文字。#include<bits/stdc++.h>
using namespace std;int a[]={1,2,3,4,5,6,7,8,9};bool check()
{int A=a[0];int B=a[1];int C=a[2];int DEF=a[3]*100+a[4]*10+a[5];int GHI=a[6]*100+a[7]*10+a[8];if(A*C*GHI+B*GHI+DEF*C==10*C*GHI)return true;elsereturn false;
}int main()
{int ans=0;do{if(check())ans++;}while(next_permutation(a,a+9));cout<<ans<<endl;return 0;
}
11李白打酒(全排列)
话说大诗人李白,一生好饮。幸好他从不开车。一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。 请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。#include <iostream>
#include <algorithm>
using namespace std;int main()
{int a[15]={-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,2,2,2,2,2};//-1遇花,2遇店int n = 0;//记录总数do{int sum = 2; //初始斗酒数for(int i=0; i<15; i++){if(a[i] == -1){sum += a[i];}else{sum *= a[i];}}if(a[14]==-1&&sum==0){ //a[14]最后一次是遇花n +=1; } }while(next_permutation(a,a+15));//全排列cout<< n << endl;return 0;
} 12、棋牌总数(递归)

#include<bits/stdc++.h>
using namespace std;int ans=0;
int sum=0;
void dfs(int x,int sum)//递归到第x层
{if(sum==13){ans++;return ;}if(x>13) return ;if(sum>13) return;for(int i=0;i<=4;i++){dfs(x+1,sum+i);}
}
int main()
{dfs(1,0);cout<<ans<<endl;return 0;
}
13、剪邮票(递归)
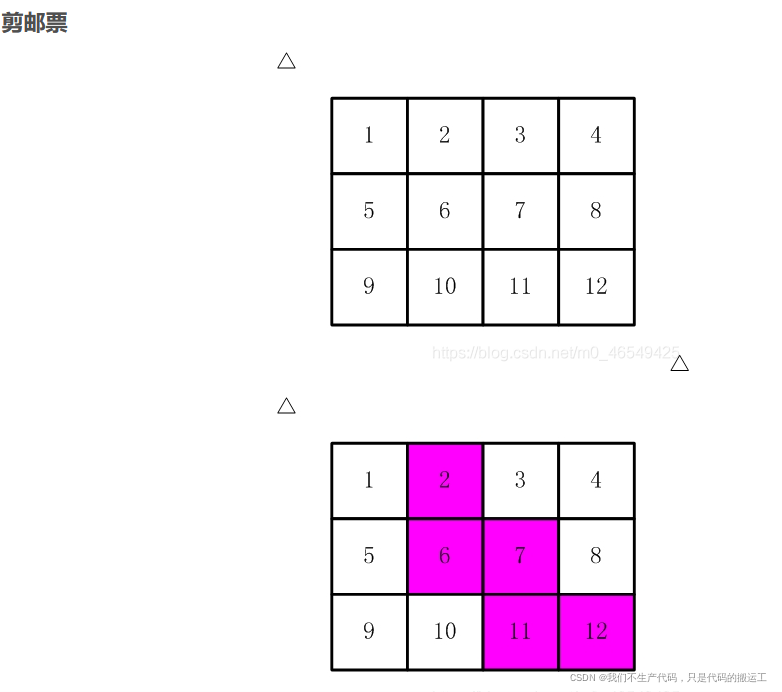
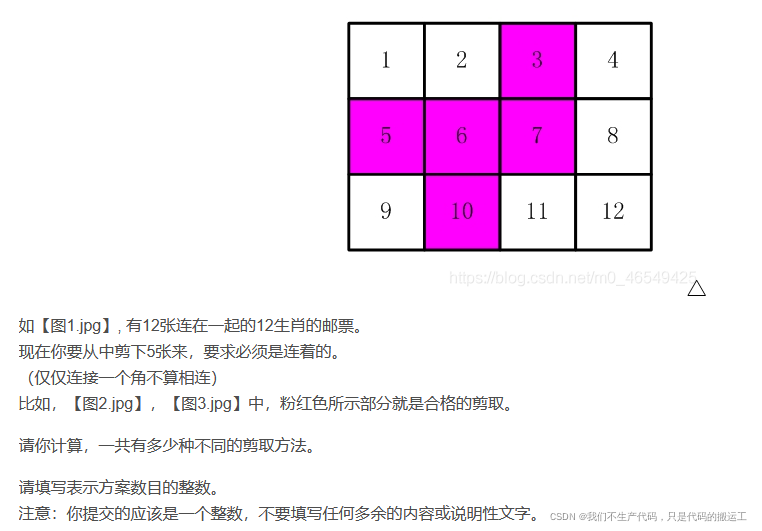
详解
#include<bits/stdc++.h>
using namespace std;
int a[]={0,0,0,0,0,0,0,1,1,1,1,1};
int f[3][4];
int dx[]={-1,0,1,0};
int dy[]={0,-1,0,1};
int ans=0;
void dfs(int a,int b)
{if(a<0||a>2||b<0||b>3)//a的取值范围[0,2] b的取值范围[0,3] return ;if(f[a][b]==0)return ;f[a][b]=0;//走过的点做标记 for(int i=0;i<4;i++){dfs(a+dx[i],b+dy[i]);}}
bool check()
{memset(f,0,sizeof(f));int k=0;for(int i=0;i<3;i++){for(int j=0;j<4;j++){f[i][j]=a[k];k++;}}int startx=0,starty=0;for(int i=0;i<3;i++)for(int j=0;j<4;j++)if(f[i][j]==1)startx=i,starty=j;dfs(startx,starty); for(int i=0;i<3;i++){for(int j=0;j<4;j++){if(f[i][j]==1)return false;}}return true;}
int main()
{do{if(check()){ans++;}}while(next_permutation(a,a+12));cout<<ans<<endl;return 0;
}
14、1050. 鸣人的影分身 (递归或动态规划(记忆化搜索))

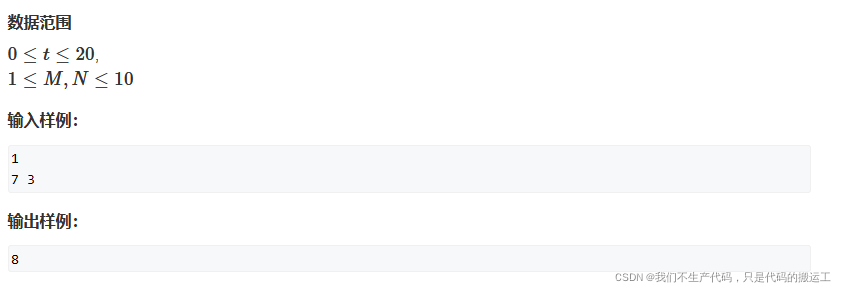
这道题目相当于是把n个苹果放m个盘子里的一道题.
题目:
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
解题分析:
设f(m,n)为m个苹果,n个盘子的放法数目,则先对n作讨论,
当n>m:则必定有n-m个盘子永远空着,去掉它们对摆放苹果方法数目不产生影响。即 if(n>m) f(m,n) = f(m,m)
当n <= m:不同的放法可以分成两类:含有0的方案数,不含有0的方案数
1、含有0的方案数,即有至少一个盘子空着,即相当于 f(m,n)=f(m,n-1);
2、不含有0的方案数,即所有的盘子都有苹果,相当于可以从每个盘子中拿掉一个苹果,不影响不同放法的数目,即 f(m,n)=f(m-n,n).而总的放苹果的放法数目等于两者的和,即 f(m,n)=f(m,n-1)+f(m-n,n)
递归出口条件说明:
当n=1时,所有苹果都必须放在一个盘子里,所以返回1;
当m==0(没有苹果可放)时,定义为1种放法;
#include<cstdio>
#include<algorithm>
#include<iostream>using namespace std;int f(int x,int y){if(x == 0) return 1;//没有能量,全部分身的能量=0if(y == 0) return 0;//必须要有 退出条件if(y > x){//分身数大于总能量数,至多只能x个分身都分一个 return f(x,x);}return f(x - y, y) + f(x, y - 1);//分身数小于等于能量数 -> //分类讨论: 任意一个分身都获得了能量 有的分身获得的能量=0,}int main(){int t,n,m;//n个能量分到m个分身里去 cin >> t;while(t --){cin >> n >> m;cout << f(n,m) << endl;}return 0;
}实际上我们可以发现,在递归的过程中就是要用到之前的数据,继而这道题可以转换为记忆化搜索将结果保存来做,即dp做法,但是这个dp是从递归去思考出来的- -而不是像灿总那样直接思考dp做法.
#include<iostream>
#include<cstdio>
using namespace std;
int a[25][25],m,n;
int main()
{int t,m,n;for(m=0;m<=10;m++){for(n=0;n<=10;n++){if(m<n)a[m][n]=a[m][m]; else if(m==0)a[m][n]=1;else if(n==0)a[m][n]=0;else a[m][n]=a[m-n][n]+a[m][n-1];}}scanf("%d",&t);for(int i=1;i<=p;i++){scanf("%d%d",&m,&n);printf("%d\n",a[m][n]);}return 0;
}15、方格分割 (dfs+思维)
题目描述:
6x6的方格,沿着格子的边线剪开成两部分。要求这两部分的形状完全相同。
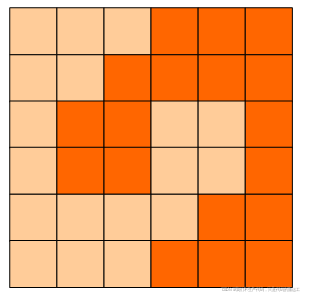
试计算:包括这3种分法在内,一共有多少种不同的分割方法。注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
如果把样例图案剪开,发现有且只有两个点在边界上,且一定经过 (3,3)点。以(3,3)为起点进行深搜,深搜到一个边界上的点,那么他的中心对称点相当于也搜过了。如果发现搜到了边界,那么它的中心对称点也到了边界 沿着已经搜过的点剪开,那么剪开的两个图形为中心对称图形。(要注意最终的结果要除以4)
例如 我们从(3,3)点出发一直向右到边界 , 或一直向左,或一直向上,或一直向下剪出来的图形是同一个。
#include<iostream>
using namespace std;
const int N=7;
int dx[]={-1,0,1,0};
int dy[]={0,-1,0,1};
int ans=0;//答案
int map[N][N]={0};//初始化
void dfs(int x,int y)//枚举分解线
{if(x==0||x==6||y==0||y==6)//退出条件 {ans++;return;} for(int i=0;i<4;i++)//四个方向{int a=x+dx[i];int b=y+dy[i];if(map[a][b]==0){map[a][b]=1;//划线 map[6-a][6-b]=1;//划线 dfs(a,b);map[a][b]=0;//恢复现场 map[6-a][6-b]=0;} }
}
int main()
{map[3][3]=1;//从中心开始,3,3表示中心的点dfs(3,3);cout<<ans/4<<endl;//注意结果除以4 旋转对称的属于同一种分割法。return 0;
}
蓝桥杯C++ AB组辅导课 第三讲 数学与简单DP
4、包子凑数
包子凑数
(1)在什么情况下,包子凑不出来的数目是无限个;
(2)如何知道包子能凑出哪些数目;
第一个问题
关键其实就是知道假如输入的每笼包子的数目不互质的话,包子凑不出来的数目就是无限个;
一直反复来求两个数的公约数,假如最后不是1,那么就说这两个数不互质,求出两个数的最大公约数之后在和后面的数又进行比较,
gcd函数返回两个或多个整数的最大公约数
第二个问题
包子凑数里面说了笼数是无穷笼,所以可以利用完全背包里面的转移方程来解决:
#include<bits/stdc++.h>
using namespace std;const int N=110;
const int INF=100100;int n;
int w[N]; //w[i]:第i种笼子所放包子数
int dp[INF]; //dp[i]能够组成的数 true 可以 false 不可以 int main()
{cin>>n;for(int i=1;i<=n;i++) cin>>w[i];memset(dp,0,sizeof(dp));int g=w[1];for(int i=2;i<=n;i++){g=__gcd(g,w[i]);}if(g!=1)cout<<"INF"<<endl;else{dp[0]=1;for(int i=1;i<=n;i++)for(int j=w[i];j<INF;j++)dp[j]=max(dp[j],dp[j-w[i]]);//背包问题转移方程变形; int res=0;for(int i=1;i<INF;i++)if(!dp[i]) res++; cout<<res<<endl; }return 0;
}
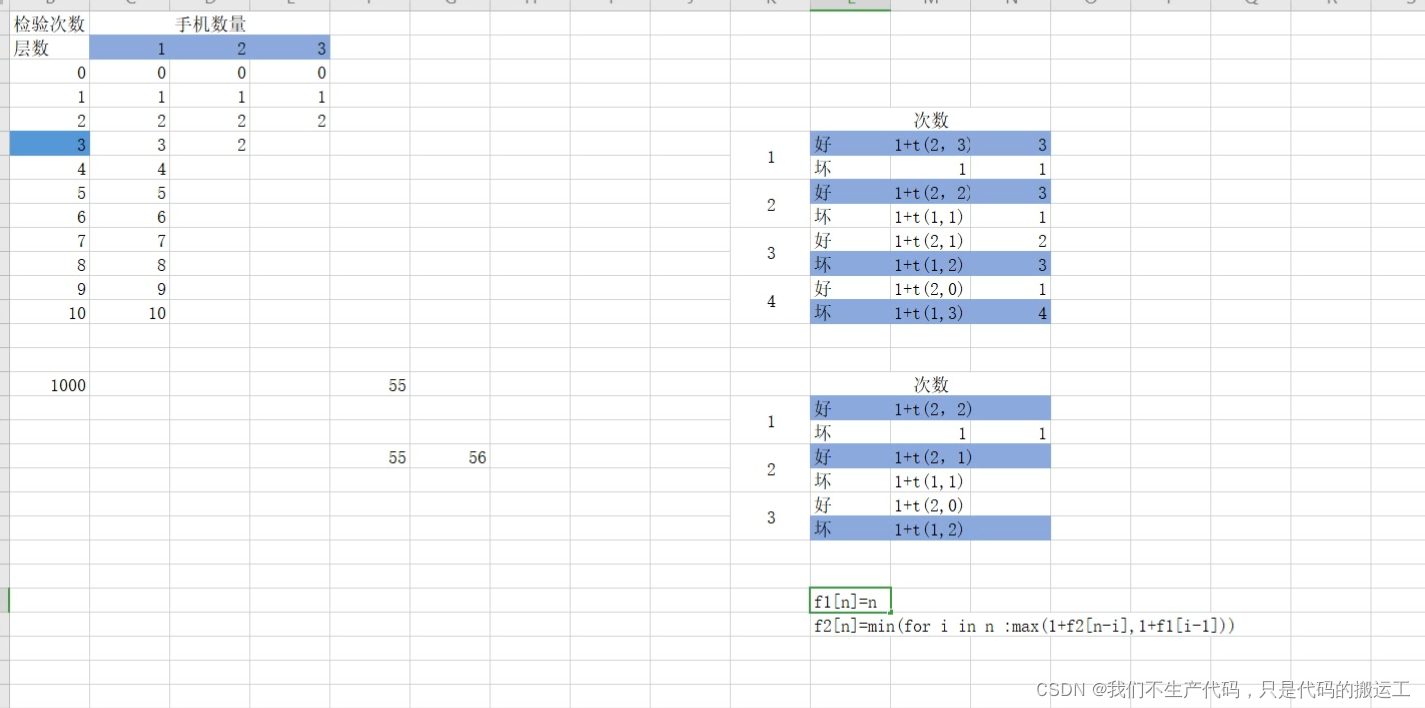
5、测试次数(最优解问题——>dp)

题解
#include<bits/stdc++.h>
using namespace std;int dp[5][1005]; // dp[i][j]: i部手机在j层摔坏的最坏次数为j次 采用最佳策略即dp
void solve(int phone,int floor)
{for(int i=1;i<=phone;i++){for(int j=1;j<=floor;j++)dp[i][j]=j; //i部手机在j层摔坏的最坏次数为j次 }for(int i=2;i<=phone;i++){for(int j=1;j<=floor;j++){for(int k=1;k<j;k++) //从第k层摔下 dp[i][j]=min(dp[i][j],max(dp[i-1][k-1],dp[i][j-k])+1);//采用最佳策略,在最坏的运气下}}
}
int main()
{solve(3,1000);cout<<dp[3][1000]<<endl;return 0;
}
数论
3、acwing2058. 笨拙的手指(进制转换)
acwing2058. 笨拙的手指(进制转换)
4、AcWing 1346. 回文平方(回文判断、进制转换)
AcWing 1346. 回文平方
视频讲解
附带的知识点和题解
6、AcWing 428. 数列(二进制,映射)
AcWing 428. 数列

#include<bits/stdc++.h>
using namespace std;int k,n;
int res=0;int power(int a,int b)//求一下a的b次方
{int res=1;while(b--) res*=a;return res;
}
int main()
{cin>>k>>n;for(int i=0;i<10;i++)//因为数据范围保持在0~1000<1024 2的10次方 {if(n>>i&1)//将n的二进制位中的第i位与上1res+=power(k,i); }cout<<res<<endl;return 0;}
7、1431分糖果
1431分糖果

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int a[N];
int b[N];bool check (int n,int a[]) {for (int i = 1;i < n; i ++) {if(a[i] != a[i+1]) {return false;}}return true;
}int main () {int n; scanf("%d", &n); for (int i = 1;i <= n; i ++) {scanf("%d", &a[i]);}int ans = 0;while (!check(n,a)) {a[0] = a[1]/2;//缓冲区存放第一个小朋友的 for(int i=1;i<n;i++)a[i]=a[i]/2+a[i+1]/2;//前n-1个小朋友的糖果传一半给前一个人 a[n]=a[n]/2+a[0];for (int i = 1; i <= n; i ++) {if(a[i] % 2 != 0) {a[i] += 1;ans ++;}}} cout << ans <<endl; return 0;
}蓝桥杯C++ AB组辅导课 第四讲 枚举、模拟与排序 Acwing
1、AcWing 1210.连号区间数(枚举)

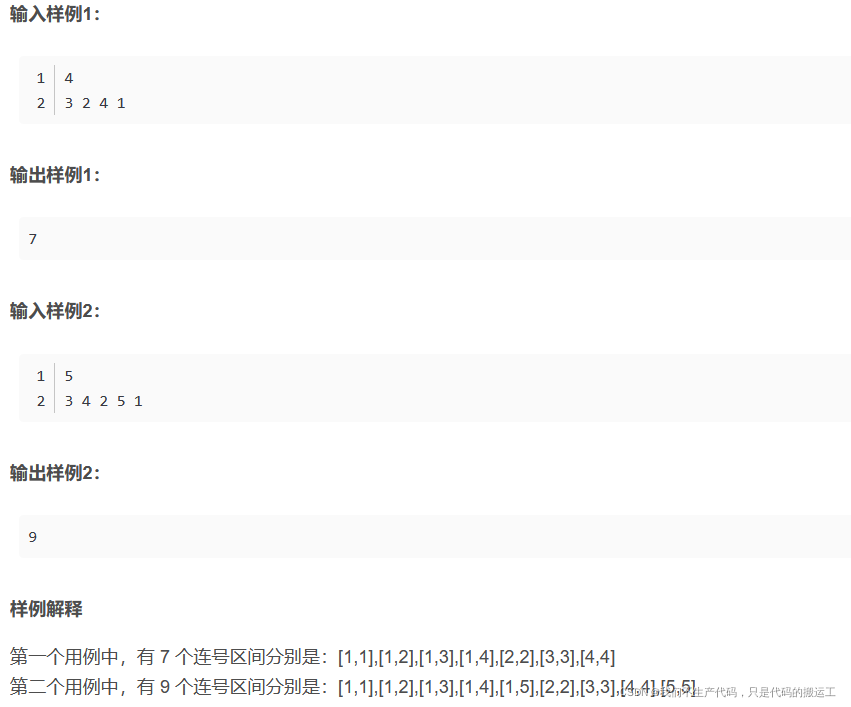
连号区间数
区间中最大值与最小值差等于区间长度
//给定的序列是包含1到N的所有数
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=1e4+10;
const int INF=0x3f3f3f3f;//定义的无穷大int n;
int a[N];
int res;//返回的答案
int main()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];//思路一个一个的枚举,枚举左右端点for(int i=1;i<=n;i++)//枚举左端点 {int maxv=-INF,minv=INF;//初始化for(int j=i;j<=n;j++)//枚举右端点{minv=min(minv,a[j]);//找到区间中的最小值maxv=max(maxv,a[j]);//找到区间中的最大值if(maxv-minv==j-i)//如果此时区间中的最大值与最小值差等于区间长度 res++; } }cout<<res<<endl; return 0;
}
5、AcWing466.回文日期(回文,日期,模拟)
AcWing466.回文日期
/*
(枚举,模拟) O(104)由于只有八位数,而且回文串左右对称,因此可以只枚举左半边,这样只需枚举 0~9999总共一万个数,然后判断:整个八位数构成的日期是否合法;是否在范围内
*/#include<iostream>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int N=1e8;
const int INF=0x3f3f3f3f;int months[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};//平年时
//判断日期是否合理
bool check(int date)//年月日组成的八位数连起来
{int year =date/10000;int month=(date%10000)/100;int day=date%100;if(month>12||month==0||day==0) return false;if(months[month]<day&&month!=2) return false;if(month==2){if(year%4==0&&year%100!=0||year%400==0){if(day>29) return false;}else{if(day>28) return false;} }return true;} int main()
{int date1, date2;cin>>date1>>date2;int res=0;for(int i=0;i<10000;i++){int x=i,r=i;for(int j=0;j<4;j++) r=r*10+x%10,x/=10;if(r>=date1&&r<=date2&&check(r)) res++;}cout<<res<<endl;return 0;
}7、AcWing1229.日期问题(字符串+时间格式)
AcWing1229.日期问题
set输出默认按字典序输出
/*
日期问题
https://www.acwing.com/problem/content/description/1231/
*/
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
set<string> ans;//用于存储最终可能的结果的集合
//字符串转化为int类型数据
int sti(string str)
{int s;stringstream ss;ss<<str; //将str输入到字符流中去ss>>s; //将ss输出到int类型的数据s中 return s;
}
//int类型转化为字符串数据
string its(int s)
{string str;stringstream ss;ss<<s;ss>>str;return str;}
//判断是否是闰年 是true
bool check(int y)
{if(y%4==0&&y%100!=0||y%400==0)return true;elsereturn false;
}
//模拟12个月份
int months[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};void getans(int y,int m,int d)
{string year,month,day;//年 判断二十世纪或者二十一世纪 if(y>=60) y+=1900;else y+=2000;//月if(m<1||m>12) return ;if(check(y))months[2]=29;elsemonths[2]=28;if(d<1||d>months[m]) return ;//注意格式 year=its(y);if(m<=9)month="0"+its(m);elsemonth=its(m);if(d<=9)day="0"+its(d);else day=its(d);string cnt=year+"-"+month+"-"+day;
//存储答案 ans.insert(cnt);}
int main()
{string str;cin>>str;int a = sti(str.substr(0,2));//可以理解为从第a个字符开始截取后面所有的字符串。int b = sti(str.substr(3,5));int c = sti(str.substr(6));//cout<<a<<" "<<b<<" "<<c<<endl;
//仅有三种格式 年月日 --- 日月年 --- 月日年 getans(a,b,c);getans(c,a,b);getans(c,b,a);for(auto x:ans)cout<<x<<endl;}
图论
1、acwing2019. 拖拉机(最短路径+双向队列)
acwing2019. 拖拉机(最短路径)
往年题目汇总
2015-2018
2015-2018
2012-2019
2013年
2013
2018年
2018
2019年
2019
2020年
2020
2021年
2021
(8)、其他进制转化为十进制
十进制转化成其他进制:短除法
// 将数字转换为字符
char get(int x)
{if(x <= 9) return x + '0';else return x - 10 + 'A';
}
// 进制转换,十进制转换为b进制
string base(int n,int b)
{string num;while(n){num += get(n % b), n /= b;//num中保留余数}reverse(num.begin(),num.end());//逆置一下numreturn num;
}
其他进制转化成十进制:秦九韶算法
// 将字符转换为数字
int uget(char c)
{if(c <= '9') return c - '0';return c - 'A' + 10;
}// 将b进制转换为十进制,秦九韶算法
int base10(string num, int b)
{int res = 0;for(auto c : num)//从高位到低位 ,枚举一位res = res * b + uget(c);return res;
}
int get(string s,int b)//将其他进制转化为十进制算法
{int res=0;//秦九韶算法 for(auto c:s)res = res * b + c - '0';//平时所用的进制转换 需要将c(字符)转化为数字 return res;
}
问题:acwing:笨拙的手指