给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4 输出:2
示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 231 - 1
一、信息
1.给我的是非负整数x
2.计算x的算术平方根
3.返回类型是整型
二、分析
条件1:告诉我不用考虑输入为负数
条件2:告诉我两点。第一点就是告诉我是算术平方根如果只是普通的平方根输出的时候还要输出正负两个答案。第二点就是告诉我此次的目的。
条件3 告诉我函数的返回值类型。
三、算法步骤:
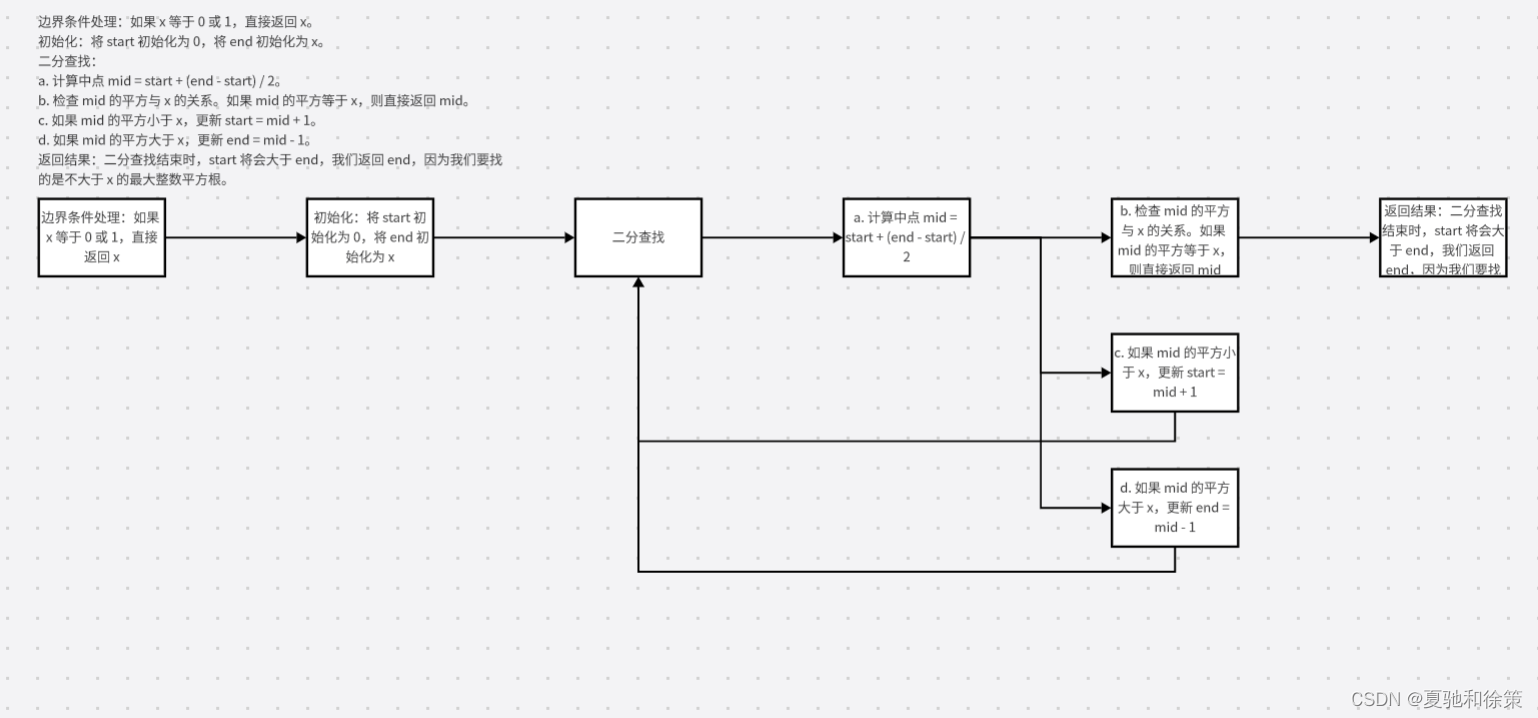
流程图:
四、问题出现
问题1.该如何实现开方呢?
我的思路:
我看到了在我面前有两条路。
第一条:遍历
我们设x为目标y为被开方的数,我们假设存在0<x<y使得x*x=y,我们只需要再y中一遍一遍试就行。这样的话时间复杂度应该为O(n).
第二条:遍历后用二分法提高查找效率。
更正后的思考过程
一、信息
我们要实现一个函数,这个函数接收一个非负整数 `x` ,计算并返回 `x` 的算术平方根的整数部分。我们不能使用内置的指数函数和算符,例如 `pow(x, 0.5)` 或者 `x ** 0.5`。
二、分析
初始思考:
一开始,我思考的是如何在没有使用平方根函数的情况下得到一个数的平方根。考虑到平方根的定义是,对于一个非负数 `x` ,其平方根是另一个非负数,这个数的平方等于 `x`。于是我们需要找到一个数,使其平方最接近且不大于 `x`。
#### 遇到的问题:
1. 我们不能直接计算平方根,所以我们需要使用一些间接的方法来找到这个数。
2. 我们需要考虑效率问题。例如,我们可以从 `0` 开始,一点一点地增加,直到我们找到这个数。但是这种方法效率很低,特别是当 `x` 很大时。
#### 解决方案:
考虑到效率问题,我们可以使用二分查找法。我们知道,对于一个非负整数 `x` ,其平方根不会大于 `x/2 + 1`。所以我们可以在 `0` 到 `x/2 + 1` 之间进行二分查找。这将大大减少我们需要检查的数字的数量,从而提高效率。
三、算法步骤
1. **边界条件处理**:如果 `x` 等于 `0` 或 `1`,直接返回 `x`。
2. **初始化**:将 `start` 初始化为 `0`,将 `end` 初始化为 `x`。
3. **二分查找**:
a. 计算中点 `mid = start + (end - start) / 2`。
b. 检查 `mid` 的平方与 `x` 的关系。如果 `mid` 的平方等于 `x`,则直接返回 `mid`。
c. 如果 `mid` 的平方小于 `x`,更新 `start = mid + 1`。
d. 如果 `mid` 的平方大于 `x`,更新 `end = mid - 1`。
4. **返回结果**:二分查找结束时,`start` 将会大于 `end`,我们返回 `end`,因为我们要找的是不大于 `x` 的最大整数平方根。
通过这个方法,我们可以高效地找到一个数的平方根的整数部分,而无需使用任何内置的平方根函数或算符。
五、实现
我的答案:
C语言版本:
#include <stdio.h>int mySqrt(int x) {if (x == 0 || x == 1) return x;long long start = 0;long long end = x;while (start <= end) {long long mid = start + (end - start) / 2;if (mid * mid == x) return mid; // 找到了精确的平方根if (mid * mid < x) {start = mid + 1;} else {end = mid - 1;}}// 由于题目要求返回整数部分,所以返回endreturn end;
}int main() {int x1 = 4;int x2 = 8;printf("The square root of %d is %d\n", x1, mySqrt(x1)); // 输出:2printf("The square root of %d is %d\n", x2, mySqrt(x2)); // 输出:2return 0;
}
C++版本:
#include <iostream>class Solution {
public:int mySqrt(int x) {if (x == 0 || x == 1) return x;long long start = 0, end = x;while (start <= end) {long long mid = start + (end - start) / 2;if (mid * mid == x) return mid; // 找到了精确的平方根if (mid * mid < x) start = mid + 1;else end = mid - 1;}// 返回end,因为我们要返回的是不大于x的最大整数平方根return end;}
};int main() {Solution solution;std::cout << "The square root of 4 is " << solution.mySqrt(4) << std::endl; // 输出:2std::cout << "The square root of 8 is " << solution.mySqrt(8) << std::endl; // 输出:2return 0;
}
JAVA:
public class Solution {public int mySqrt(int x) {if (x == 0 || x == 1) return x;long start = 0, end = x;while (start <= end) {long mid = start + (end - start) / 2;if (mid * mid == x) return (int) mid; // 找到了精确的平方根if (mid * mid < x) start = mid + 1;else end = mid - 1;}// 返回end,因为我们要返回的是不大于x的最大整数平方根return (int) end;}public static void main(String[] args) {Solution solution = new Solution();System.out.println("The square root of 4 is " + solution.mySqrt(4)); // 输出:2System.out.println("The square root of 8 is " + solution.mySqrt(8)); // 输出:2}
}
Leetcode 题解:
方法三:牛顿迭代

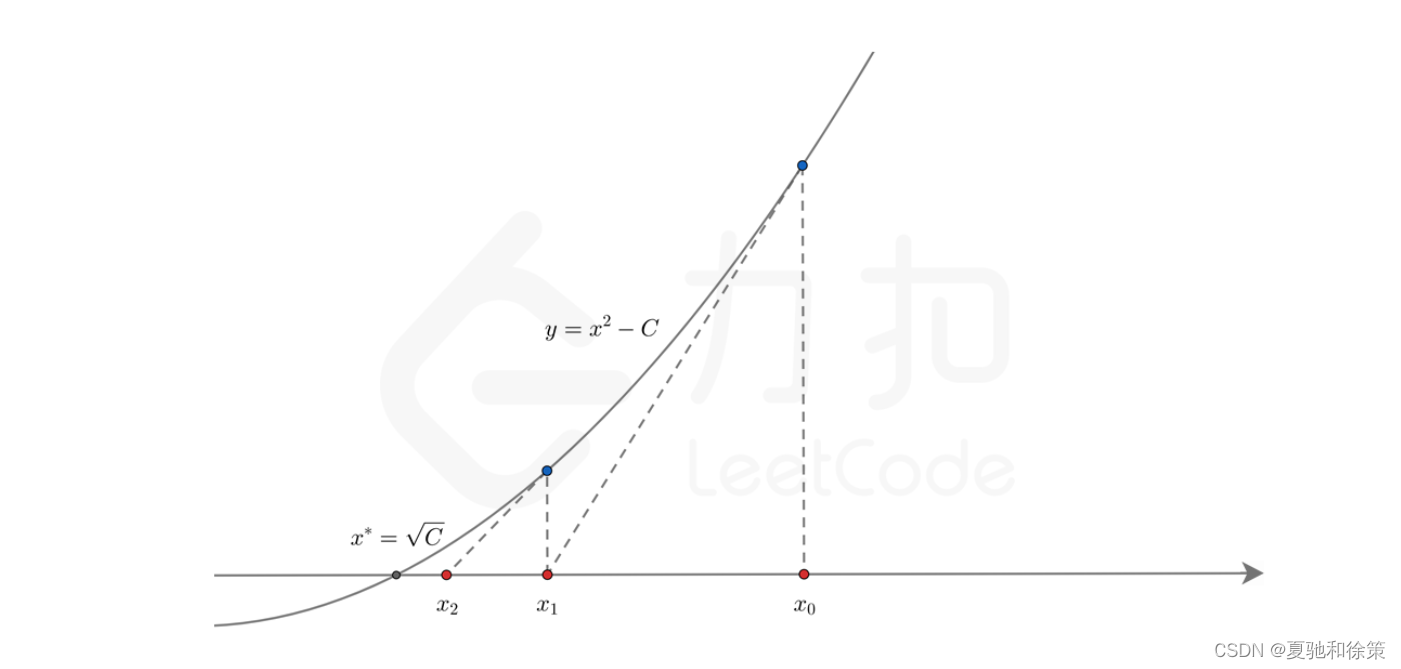


源代码:
class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}double C = x, x0 = x;while (true) {double xi = 0.5 * (x0 + C / x0);if (fabs(x0 - xi) < 1e-7) {break;}x0 = xi;}return int(x0);}
};我的答案和Leetcode的答案的各自的优劣
二分查找法和牛顿迭代法都是有效的数值方法,用于求解平方根,它们各自有一些优劣势:
### 1. **二分查找法**:
#### 优势:
- **直观易懂**:二分查找法是一种非常直观且易于理解和实现的算法。
- **稳定性高**:由于算法逻辑简单,因此其在各种情况下都表现得很稳定。
- **适用性广**:二分查找法可以应用于任何有序序列,不仅仅局限于求平方根。
#### 劣势:
- **收敛速度**:相较于牛顿迭代法,二分查找法的收敛速度较慢,尤其是在求解较大的数的平方根时。
### 2. **牛顿迭代法**:
#### 优势:
- **收敛速度快**:牛顿迭代法是一种二次收敛的方法,每一次迭代都会使得结果的有效数字大约翻倍,因此通常会比二分查找法更快地收敛到实际的平方根。
- **适用性强**:牛顿迭代法可以用来求解各种非线性方程的根,适用性非常广泛。
#### 劣势:
- **实现复杂度**:相较于二分查找法,牛顿迭代法的实现略显复杂。
- **初始值选择**:牛顿迭代法的收敛性会受到初始值选择的影响,而选择合适的初始值有时并非易事。
### 综合比较:
对于求平方根这一特定问题而言,如果追求算法的简单和稳定,二分查找是一个很好的选择。而如果追求更高的收敛速度,尤其是在处理较大的数时,牛顿迭代法会是更优的选择。在实际应用中,可以根据问题的具体要求和约束来选择最合适的方法。
总结:
从这道题目中,我们能学到多方面的知识和技能:
### 1. **算法基础**
- **二分查找**:学会使用二分查找来求解有序序列中的问题,理解其工作原理和实现方法。
- **牛顿迭代**:学会使用牛顿迭代法来快速求解非线性方程的根,理解其收敛性和收敛速度。
### 2. **编程实践**
- **实现方法**:学会如何将算法用代码实现,例如C++或Java中如何实现二分查找和牛顿迭代法。
- **调试和优化**:通过实践,学会如何调试代码,优化算法性能,如何选择合适的初始值和终止条件等。
### 3. **数学知识**
- **函数和图像理解**:通过牛顿迭代法,加深对函数、导数和图像的理解,学习如何通过图像直观理解算法过程。
- **收敛性理解**:通过对比不同方法,理解算法的收敛性和收敛速度,学会如何评估算法的性能。
### 4. **问题解决技能**
- **多种解决方案**:学会对同一问题采用不同的解决方案,并能够分析各种方案的优劣,从而选择最合适的一种。
- **分析和评估**:学会分析问题的需求和限制,评估不同方案的适用性,做出合理的决策。
### 5. **实际应用**
- **实际问题中的应用**:学会如何将学到的算法和知识应用到实际问题中,例如在没有开方运算的环境中求解平方根。
- **性能优化**:了解在实际应用中如何优化算法,提高算法的运行效率,满足实际需求。
总之,这道题目不仅可以加深对基础算法和编程的理解,而且可以提高数学理论和问题解决能力,具有很高的学习价值。







![[Linux 基础] 一篇带你了解linux权限问题](https://img-blog.csdnimg.cn/5bd35aa61ce14a17b0dd42d08bd59bf2.png)