傅里叶系列 P1 的定价选项

如果您想了解更多信息，请查看第 2 部分和第 3 部分。

一、说明

这是第一篇文章，我将帮助您获得如何使用这个新的强大工具来解决金融中的半分析问题并取代您的蒙特卡洛方法的直觉。

我们都知道并喜欢蒙特卡洛数字积分方法，但是如果我告诉你你可以用虚数和傅里叶级数来代替蒙特卡洛呢？
主要好处是速度，这在期权定价中非常重要。这非常重要，因为用于定价股票期权的赫斯顿模型需要数字积分，蒙特卡罗大约需要 100 毫秒，傅里叶级数需要几毫秒。

二、第 1 部分：但是什么是傅里叶级数？

对于任何函数 f 和区间 a，b，我们可以将 f（x） 近似为余弦和正弦的无限和，L = b-a。

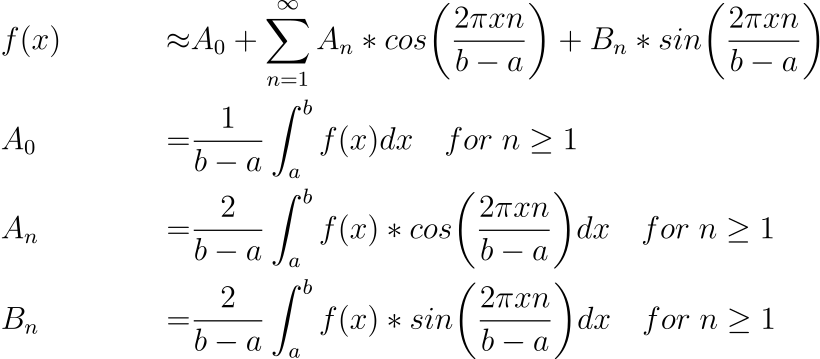
三、第 2 部分：将数学公式应用于 Python


def get_fourier_approx(f, x:np.array, a:float, b:float, N:int):fa = lambda x, n : f(x) * cos((2*pi*n*x)/(b - a))fb = lambda x, n : f(x) * sin((2*pi*n*x)/(b - a))A0 = 1/(b - a) * quad(f, a, b, limit=200)[0]Cosine_Sine_Sum = np.zeros_like(x)for n in range(1, N+1):A = 2/(b - a) * quad(fa, a, b, args=(n), limit=200)[0]B = 2/(b - a) * quad(fb, a, b, args=(n), limit=200)[0]Cosine_Sine_Sum += A*cos((2*pi*n*x)/(b - a)) + B*sin((2*pi*n*x)/(b - a))fx = A0 + Cosine_Sine_Sumreturn fx

a = -6
b = 6
x = np.linspace(a, b, 1_000)
y = f(x)fig, (ax1, ax2) = plt.subplots(2, figsize=(20,12))
blue_shades = ['#0000FF', '#3399FF', '#66B2FF', '#99CCFF', '#CCE5FF']avg_residuals = []
Ns = [8, 16, 32, 64, 128]
for i, N in enumerate(Ns):fx = get_fourier_approx(f=f, x=x, a=a, b=b, N=N)ax1.plot(x,fx, blue_shades[i], label=f'N = {N}')ax2.plot(x,y-fx, blue_shades[i], label=f'N = {N}')avg_residuals.append(np.abs(y-fx).mean())ax1.set_title('Fourier Transform of f(x)')
ax1.plot(x,y,'tab:red', linestyle='--')
ax2.set_title('Residuals')
plt.tight_layout() ; ax1.legend();ax2.legend() ; plt.show()pd.Series(avg_residuals, index=Ns, name='Avg Residual')

3.1 方形功能：

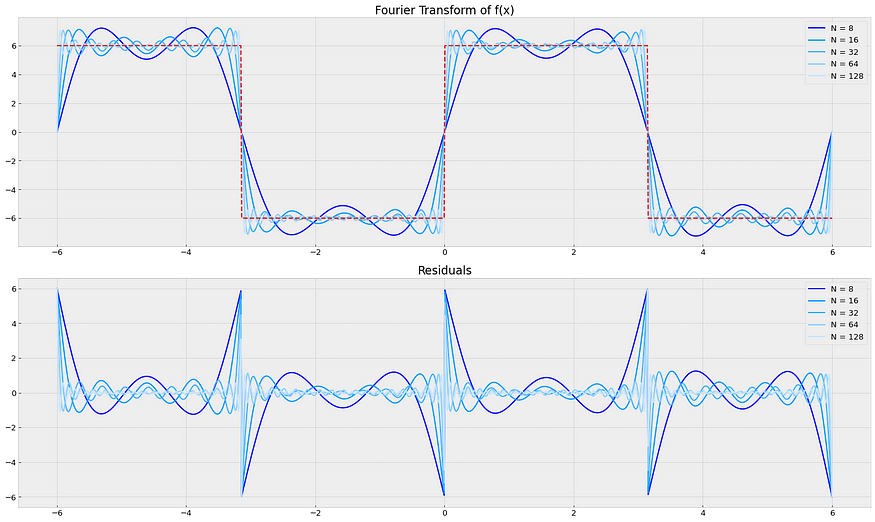
来源：笔记本

N      Avg. Residual
--------------------
8      1.311711
16     0.784683
32     0.440387
64     0.268449
128    0.154604

3.2 线路功能：

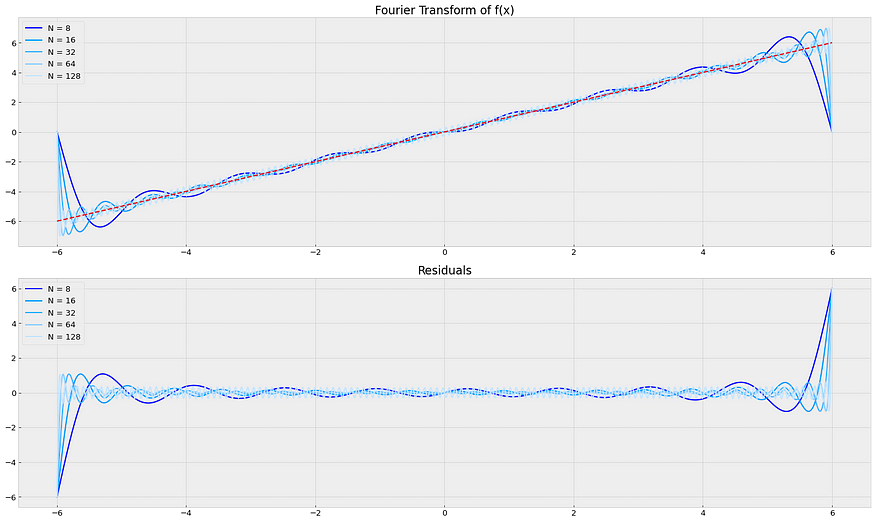
来源：笔记本

N      Avg. Residual
--------------------
8      0.447389
16     0.264635
32     0.153540
64     0.088745
128    0.052147

3.3 正态分布

在 [0， 12] 中缩放 y，其中：
- 平均值 = 100- 标准 = 0.1 *sqrt（5）*100- a = 100 -12 * 标准
- b = 100

+12 * 标准

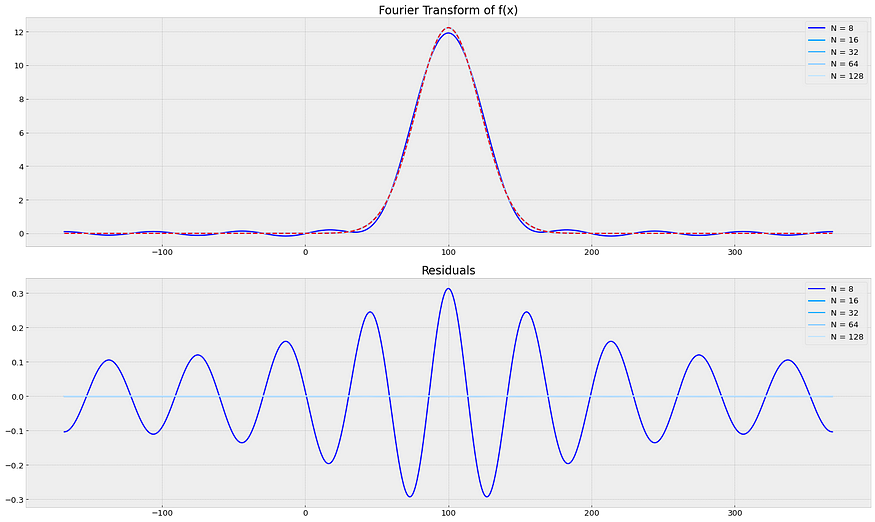
来源：笔记本

N      Avg. Residual
--------------------
8      1.092374e-01
16     8.326020e-05
32     6.878539e-14
64     5.721031e-14
128    5.170898e-14

3.3 议论

所有分布都按比例缩放，使 y 范围从 [0,12] 开始，因此我们可以比较残差的大小。
从绘图和残差可以看出，函数的曲线越大，傅里叶级数收敛到正确值的速度就越快。我们将此属性用作正态，并且对数正态不需要很多项来计算，在我们的近似中具有足够的准确性。
数据开头和结尾的误差明显更高。因此，最好包含比预期使用的限制更高的限制。例如，当您需要 ±4 时计算 ±3std。这使得深度价外期权更难计算。

四、第3部分 S（T）的对数正态分布

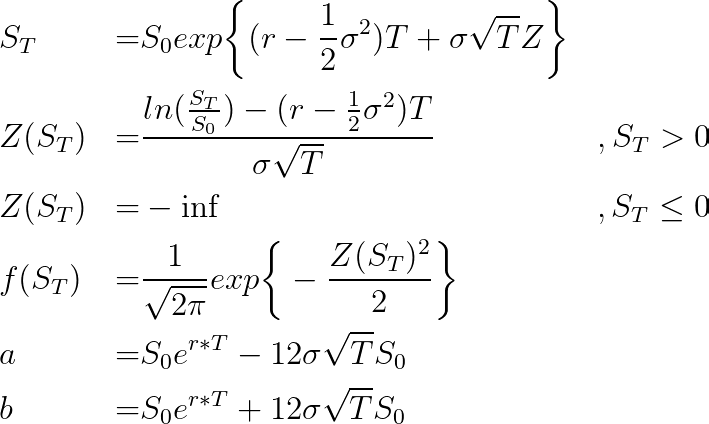
S_T遵循 Q 下的简单 GBM，我们可以使用以下等式推导出S_T的概率密度：

现在我们可以使用以下函数在 Python 中定义 f（S_T），并将下限定义为（ 0， S_0*exp（r*T） + 12 * sigma*sqrt（T）*S_0 ）

S0      = 100
r       = 0.05
sigma   = 0.1
T       = 5.0Z = lambda St : np.where(St > 0, ((log(St/S0) - (r - .5*sigma)*T)/(sqrt(T)*sigma)), -np.inf)
f = lambda x : norm.pdf(Z(x))a   = S0*exp(r*T) - 12 * sigma*sqrt(T)*S0
b   = S0*exp(r*T) + 12 * sigma*sqrt(T)*S0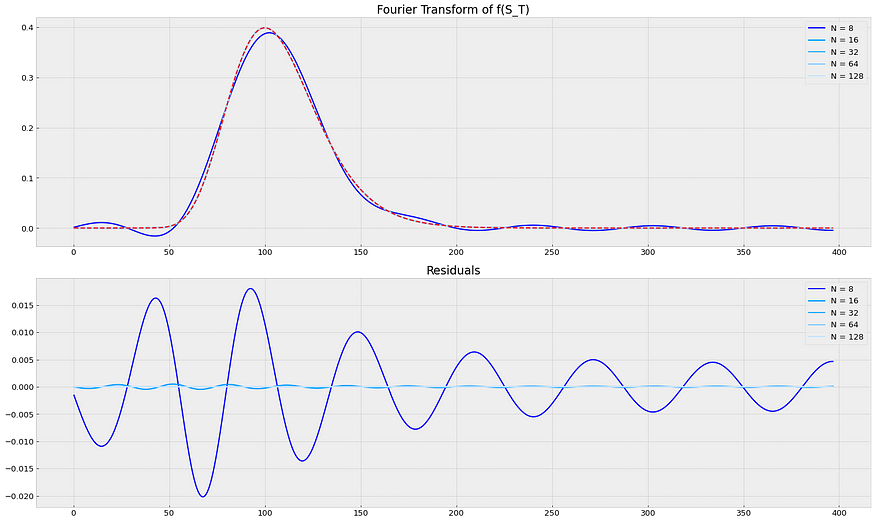

Source: Notebook

N       Avg. (scaled) Residual      Avg. Residual       Execution Time (sec)
----------------------------------------------------------------------------
8       0.176429                    5.880975e-03        0.112720
16      0.004235                    1.411566e-04        0.246473
32      0.000030                    9.855127e-07        0.624209
64      0.000027                    8.918504e-07        1.936948
128     0.000026                    8.530034e-07        6.741019

4.1 言论：

我包括了缩放和非缩放残差。缩放残差对应于（不正确的）缩放概率，使得 max{y}=12，其中（正确的）非缩放，max{y}=0.4。这样做是为了将对数正态分布的拟合与上面绘制的其他函数进行比较。
我们可以推断出，由于形状不对称，对数正态分布比正态分布更难拟合。
我们可以看到，在非缩放版本中有 64 项，计算 P（S_T=x）的预期误差非常小，小于 0.0001%。
将分布集中在 T 处的期望值周围非常重要，12stds 左右对称。 我做了一个版本，其中a和b不对称，残差不均匀分布。直觉上，你会采取 a=0+，但它不会产生理想的结果。*S_T残差是针对 S_T>0 的值计算的，因为这是不可能的，我们不关心小于 0 的值。

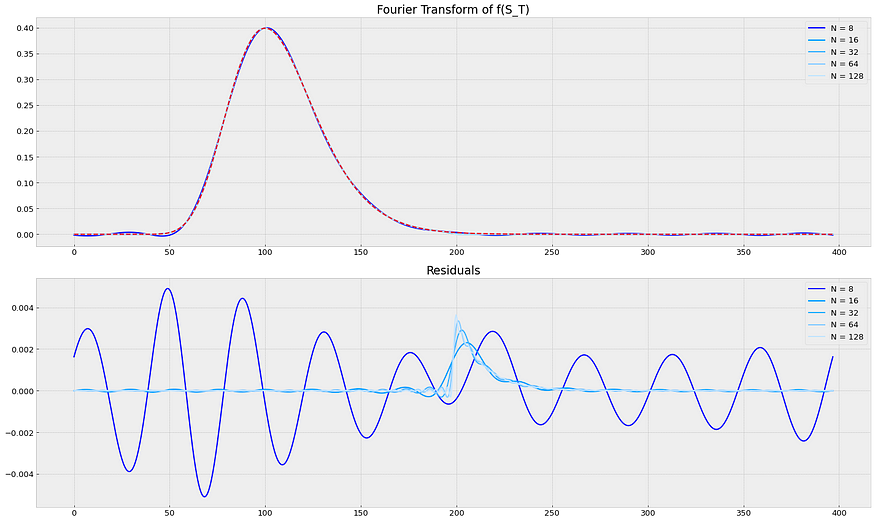
a=1e-8 的S_T密度，在残差处表现出不良性质。来源：笔记本

4.2 限制 — 缺点 — 改进：

将前面提到的任何函数近似为傅里叶级数并使用数值积分作为计算 An 和 Bn 的手段没有任何好处。
分析计算 An 和 Bn 系数非常重要，因此唯一的数值部分是计算序列。
好处在别处。当f（x）没有显式形式并且需要数值积分时，我们可以用特征函数和傅里叶级数半解析地解决问题。
如果我们在 Python 中使用 scipy.norm 为带有标准 BS 的选项定价，大约需要 0.06 毫秒。
但是，如果我们解析求解积分 A0、An、Bn 并使用复数版本，我们会得到大约 0.6 毫秒，这是可比的。我们将在第 3 部分中在 Heston 模型中使用它，该模型是此类期权定价的行业标准。