15 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意: 答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
思路
本题若采用哈希来解决,在处理去重的时候会比较复杂,所以本题考虑容易理解的双指针法。
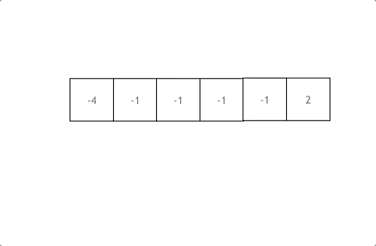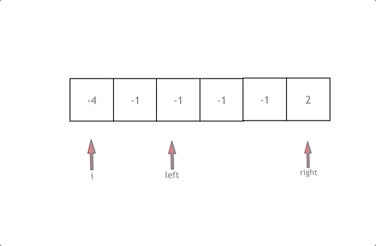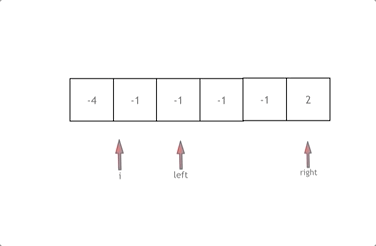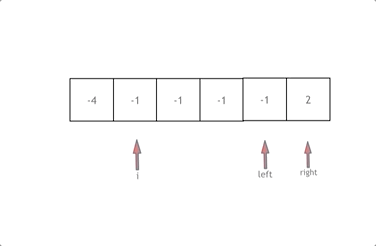
拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
时间复杂度:O(n^2)。(有两层循环)
关于去重逻辑的思考可参考:https://www.programmercarl.com/0015.%E4%B8%89%E6%95%B0%E4%B9%8B%E5%92%8C.html#%E6%80%9D%E8%B7%AF
写的很详细。
class Solution(object):def threeSum(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""# 本题的一个复杂之处是 答案中不可以包含重复的三元组# 采用双指针法 result = [] # 存储结果nums = sorted(nums) # 先对nums进行排序 可以方便很多for i in range(len(nums)): # 将i视为a 三数中的第一个数if nums[i] > 0: # 第一个数就大于0return resultif i > 0 and nums[i]==nums[i-1]: # 对a去重 跳过重复的三元组 注意是nums[i]==nums[i-1]continue left = i + 1 # 第一个指针 将left视为b 三数中的第二个数right = len(nums)-1 # 第二个指针 将right视为c 三数中的第三个数while(right > left): # 不能等于 因为要求三个数 若right=left 那就是指向同一个数sum_ = nums[i] + nums[left] + nums[right]if sum_ > 0:right -= 1 # 有点像滑动窗口elif sum_ < 0:left += 1else:result.append([nums[i], nums[left], nums[right]])# 对b去重while right > left and nums[left]==nums[left+1]:left += 1 # left就后移一位# 对c去重while right > left and nums[right]==nums[right-1]:right -= 1# 无论如何 都要移动left和rightleft += 1right -= 1return result
思考
与两数之和的区别:前面两数之和返回的是元素下标(并且题目说明:你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。),而本题三数之和返回的是具体的元素。
所以在python中,可以用集合这种数据集结构来使用哈希法,刚好又是需要索引。所以对于这种两数之和,最好的方法还是哈希法。