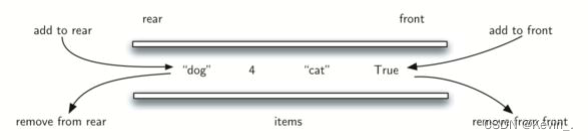
153.寻找旋转排序数组中的最小值

由于该排序数组经由1到n次旋转，所以旋转后的数组折线图为：

最小值处于中间，同时对于最后一个元素x：在最小值右侧的元素，它们的值一定严格小于x,而在最小值左侧的元素，它们的值一定严格大于x，因为是旋转数组，旋转后的最后一个值小于第一个值

因此可以使用二分查找：

第一种情况：
nums[mid] < nums[high]：说明nums[mid]是最小值右侧的元素

第二种情况：

nums[mid] > nums[high]：说明nums[mid]是最小值左侧的元素

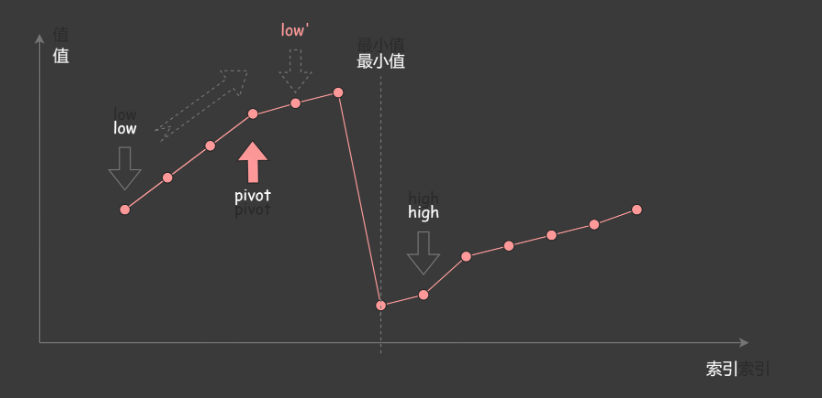
由于数组中不包含重复元素，且只要当前的区间长度不为1，mid就不会与high重合，如果当前的区间长度为1，说明已经结束二分查找，因此不会存在nums[mid]=nums[high]的情况

class Solution {public int findMin(int[] nums) {int low = 0,high = nums.length -1;while(low < high){int mid = (low + high) / 2;if(nums[mid] < nums[high]){  //如果中点的值小于nums[high]说明[mid,high]是有序的，说明最小值在mid右侧high = mid;}else{  //如果nums[mid]>nums[high]说明最小值在mid右侧，则low = mid + 1low = mid + 1;}}return nums[low];}
}