第五课 树与图

文章目录

  • 第五课 树与图
    • lc94.二叉树的中序遍历--简单
      • 题目描述
      • 代码展示
    • lc589.N叉树的层序遍历--中等
      • 题目描述
      • 代码展示
    • lc297.二叉树的序列化和反序列化--困难
      • 题目描述
      • 代码展示
    • lc105.从前序与中序遍历序列构造二叉树--中等
      • 题目描述
      • 代码展示
    • lc106.从中序与后序遍历序列构造二叉树--中等
      • 题目描述
      • 代码展示
    • lc236.二叉树的最近公共祖先（LCA）--中等
      • 题目描述
      • 代码展示
    • lc207.课程表--中等
      • 题目描述
      • 代码展示
    • lc210.课程表II--中等
      • 题目描述
      • 代码展示
    • lc684.冗余连接--中等
      • 题目描述
      • 代码展示

第五课 树与图

lc94.二叉树的中序遍历–简单

题目描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

img

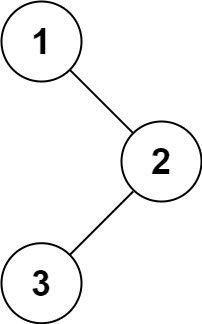
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

代码展示

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void inorder(TreeNode* root, vector<int>& res) {if (!root) {return;}inorder(root->left, res);res.push_back(root->val);inorder(root->right, res);}vector<int> inorderTraversal(TreeNode* root) {vector<int> res;inorder(root, res);return res;}
};

lc589.N叉树的层序遍历–中等

题目描述

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

img

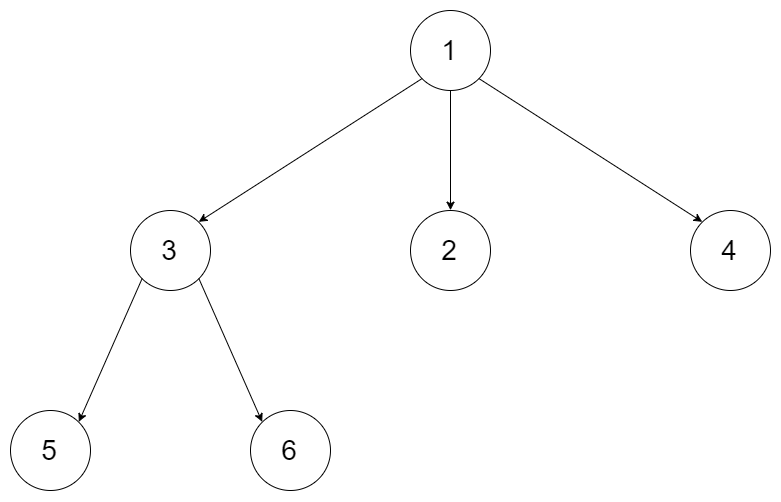
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

img

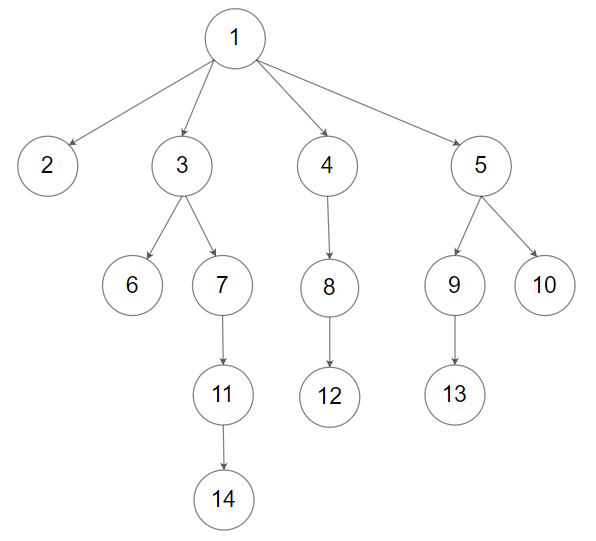
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

  • 树的高度不会超过 1000
  • 树的节点总数在 [0, 10^4] 之间

代码展示

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:     //广度优先搜索vector<vector<int>> levelOrder(Node* root) {if (!root) {return {};}vector<vector<int>> ans;queue<Node*> q;q.push(root);while (!q.empty()) {int cnt = q.size();vector<int> level;for (int i = 0; i < cnt; ++i) {Node* cur = q.front();q.pop();level.push_back(cur->val);for (Node* child: cur->children) {q.push(child);}}ans.push_back(move(level));}return ans;}
};

lc297.二叉树的序列化和反序列化–困难

题目描述

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1：

img

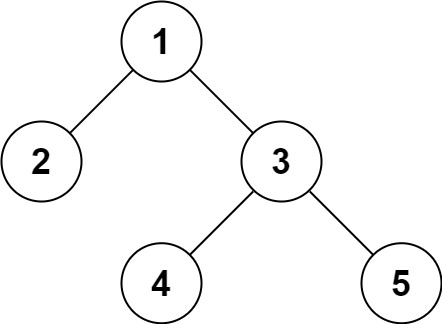
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

提示：

  • 树中结点数在范围 [0, 104] 内
  • -1000 <= Node.val <= 1000

代码展示

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Codec {
public:void rserialize(TreeNode* root, string& str) {if (root == nullptr) {str += "None,";} else {str += to_string(root->val) + ",";rserialize(root->left, str);rserialize(root->right, str);}}string serialize(TreeNode* root) {string ret;rserialize(root, ret);return ret;}TreeNode* rdeserialize(list<string>& dataArray) {if (dataArray.front() == "None") {dataArray.erase(dataArray.begin());return nullptr;}TreeNode* root = new TreeNode(stoi(dataArray.front()));dataArray.erase(dataArray.begin());root->left = rdeserialize(dataArray);root->right = rdeserialize(dataArray);return root;}TreeNode* deserialize(string data) {list<string> dataArray;string str;for (auto& ch : data) {if (ch == ',') {dataArray.push_back(str);str.clear();} else {str.push_back(ch);}}if (!str.empty()) {dataArray.push_back(str);str.clear();}return rdeserialize(dataArray);}
};// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

lc105.从前序与中序遍历序列构造二叉树–中等

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

img

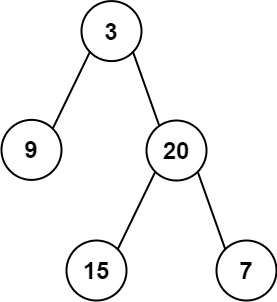
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

  • 1 <= preorder.length <= 3000
  • inorder.length == preorder.length
  • -3000 <= preorder[i], inorder[i] <= 3000
  • preorder 和 inorder 均 无重复 元素
  • inorder 均出现在 preorder
  • preorder 保证 为二叉树的前序遍历序列
  • inorder 保证 为二叉树的中序遍历序列

代码展示

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:     unordered_map<int, int> index;public:       //递归TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {if (preorder_left > preorder_right) {return nullptr;}// 前序遍历中的第一个节点就是根节点int preorder_root = preorder_left;// 在中序遍历中定位根节点int inorder_root = index[preorder[preorder_root]];// 先把根节点建立出来TreeNode* root = new TreeNode(preorder[preorder_root]);// 得到左子树中的节点数目int size_left_subtree = inorder_root - inorder_left;// 递归地构造左子树，并连接到根节点// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);// 递归地构造右子树，并连接到根节点// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = preorder.size();// 构造哈希映射，帮助我们快速定位根节点for (int i = 0; i < n; ++i) {index[inorder[i]] = i;}return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);}
};

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:       //迭代TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if (!preorder.size()) {return nullptr;}TreeNode* root = new TreeNode(preorder[0]);stack<TreeNode*> stk;stk.push(root);int inorderIndex = 0;for (int i = 1; i < preorder.size(); ++i) {int preorderVal = preorder[i];TreeNode* node = stk.top();if (node->val != inorder[inorderIndex]) {node->left = new TreeNode(preorderVal);stk.push(node->left);}else {while (!stk.empty() && stk.top()->val == inorder[inorderIndex]) {node = stk.top();stk.pop();++inorderIndex;}node->right = new TreeNode(preorderVal);stk.push(node->right);}}return root;}
};

lc106.从中序与后序遍历序列构造二叉树–中等

题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

img

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

  • 1 <= inorder.length <= 3000
  • postorder.length == inorder.length
  • -3000 <= inorder[i], postorder[i] <= 3000
  • inorder 和 postorder 都由 不同 的值组成
  • postorder 中每一个值都在 inorder 中
  • inorder 保证是树的中序遍历
  • postorder 保证是树的后序遍历

代码展示

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {int post_idx;unordered_map<int, int> idx_map;
public:     //递归TreeNode* helper(int in_left, int in_right, vector<int>& inorder, vector<int>& postorder){// 如果这里没有节点构造二叉树了，就结束if (in_left > in_right) {return nullptr;}// 选择 post_idx 位置的元素作为当前子树根节点int root_val = postorder[post_idx];TreeNode* root = new TreeNode(root_val);// 根据 root 所在位置分成左右两棵子树int index = idx_map[root_val];// 下标减一post_idx--;// 构造右子树root->right = helper(index + 1, in_right, inorder, postorder);// 构造左子树root->left = helper(in_left, index - 1, inorder, postorder);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {// 从后序遍历的最后一个元素开始post_idx = (int)postorder.size() - 1;// 建立（元素，下标）键值对的哈希表int idx = 0;for (auto& val : inorder) {idx_map[val] = idx++;}return helper(0, (int)inorder.size() - 1, inorder, postorder);}
};

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:        //迭代TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (postorder.size() == 0) {return nullptr;}auto root = new TreeNode(postorder[postorder.size() - 1]);auto s = stack<TreeNode*>();s.push(root);int inorderIndex = inorder.size() - 1;for (int i = int(postorder.size()) - 2; i >= 0; i--) {int postorderVal = postorder[i];auto node = s.top();if (node->val != inorder[inorderIndex]) {node->right = new TreeNode(postorderVal);s.push(node->right);} else {while (!s.empty() && s.top()->val == inorder[inorderIndex]) {node = s.top();s.pop();inorderIndex--;}node->left = new TreeNode(postorderVal);s.push(node->left);}}return root;}
};

lc236.二叉树的最近公共祖先（LCA）–中等

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

img

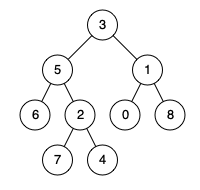
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

img

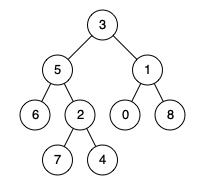
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

  • 树中节点数目在范围 [2, 105] 内。
  • -109 <= Node.val <= 109
  • 所有 Node.val 互不相同 。
  • p != q
  • p 和 q 均存在于给定的二叉树中。

代码展示

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:        //递归TreeNode* ans;bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == nullptr) return false;bool lson = dfs(root->left, p, q);bool rson = dfs(root->right, p, q);if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))) {ans = root;} return lson || rson || (root->val == p->val || root->val == q->val);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {dfs(root, p, q);return ans;}
};

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:        //存储父节点unordered_map<int, TreeNode*> fa;unordered_map<int, bool> vis;void dfs(TreeNode* root){if (root->left != nullptr) {fa[root->left->val] = root;dfs(root->left);}if (root->right != nullptr) {fa[root->right->val] = root;dfs(root->right);}}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {fa[root->val] = nullptr;dfs(root);while (p != nullptr) {vis[p->val] = true;p = fa[p->val];}while (q != nullptr) {if (vis[q->val]) return q;q = fa[q->val];}return nullptr;}
};

image-20231007134941860

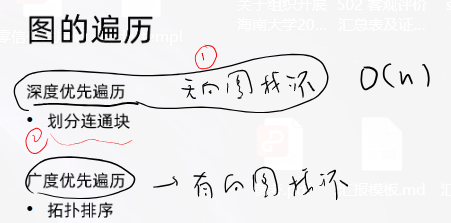
image-20231007134949007

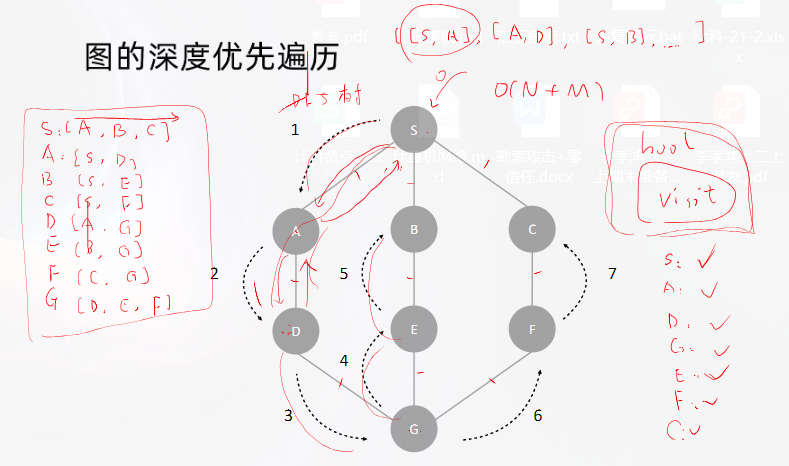
image-20231007135002466

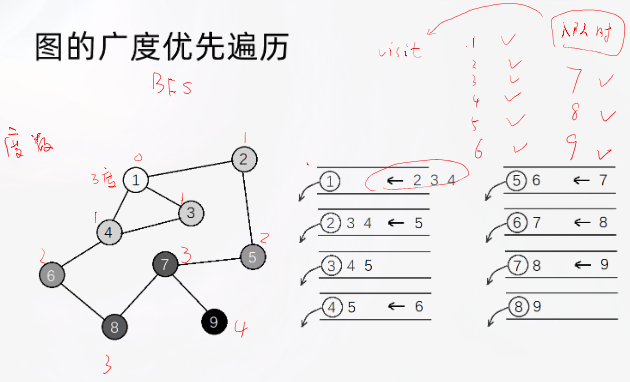
image-20231007135017309

lc207.课程表–中等

题目描述

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

  • 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

  • 1 <= numCourses <= 2000
  • 0 <= prerequisites.length <= 5000
  • prerequisites[i].length == 2
  • 0 <= ai, bi < numCourses
  • prerequisites[i] 中的所有课程对 互不相同

代码展示

class Solution {
private:vector<vector<int>> edges;vector<int> visited;bool valid = true;public:       //深度优先搜索void dfs(int u) {visited[u] = 1;for (int v: edges[u]) {if (visited[v] == 0) {dfs(v);if (!valid) {return;}}else if (visited[v] == 1) {valid = false;return;}}visited[u] = 2;}bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {edges.resize(numCourses);visited.resize(numCourses);for (const auto& info: prerequisites) {edges[info[1]].push_back(info[0]);}for (int i = 0; i < numCourses && valid; ++i) {if (!visited[i]) {dfs(i);}}return valid;}
};

class Solution {
private:vector<vector<int>> edges;vector<int> indeg;public:       //广度优先搜索bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {edges.resize(numCourses);indeg.resize(numCourses);for (const auto& info: prerequisites) {edges[info[1]].push_back(info[0]);++indeg[info[0]];}queue<int> q;for (int i = 0; i < numCourses; ++i) {if (indeg[i] == 0) {q.push(i);}}int visited = 0;while (!q.empty()) {++visited;int u = q.front();q.pop();for (int v: edges[u]) {--indeg[v];if (indeg[v] == 0) {q.push(v);}}}return visited == numCourses;}
};

lc210.课程表II–中等

题目描述

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。

  • 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2：

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

示例 3：

输入：numCourses = 1, prerequisites = []
输出：[0]

提示：

  • 1 <= numCourses <= 2000
  • 0 <= prerequisites.length <= numCourses * (numCourses - 1)
  • prerequisites[i].length == 2
  • 0 <= ai, bi < numCourses
  • ai != bi
  • 所有[ai, bi] 互不相同

代码展示

class Solution {
private:// 存储有向图vector<vector<int>> edges;// 标记每个节点的状态：0=未搜索，1=搜索中，2=已完成vector<int> visited;// 用数组来模拟栈，下标 0 为栈底，n-1 为栈顶vector<int> result;// 判断有向图中是否有环bool valid = true;public:          //深度优先搜索void dfs(int u) {// 将节点标记为「搜索中」visited[u] = 1;// 搜索其相邻节点// 只要发现有环，立刻停止搜索for (int v: edges[u]) {// 如果「未搜索」那么搜索相邻节点if (visited[v] == 0) {dfs(v);if (!valid) {return;}}// 如果「搜索中」说明找到了环else if (visited[v] == 1) {valid = false;return;}}// 将节点标记为「已完成」visited[u] = 2;// 将节点入栈result.push_back(u);}vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {edges.resize(numCourses);visited.resize(numCourses);for (const auto& info: prerequisites) {edges[info[1]].push_back(info[0]);}// 每次挑选一个「未搜索」的节点，开始进行深度优先搜索for (int i = 0; i < numCourses && valid; ++i) {if (!visited[i]) {dfs(i);}}if (!valid) {return {};}// 如果没有环，那么就有拓扑排序// 注意下标 0 为栈底，因此需要将数组反序输出reverse(result.begin(), result.end());return result;}
};

class Solution {
private:// 存储有向图vector<vector<int>> edges;// 存储每个节点的入度vector<int> indeg;// 存储答案vector<int> result;public:         //广度优先搜索vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {edges.resize(numCourses);indeg.resize(numCourses);for (const auto& info: prerequisites) {edges[info[1]].push_back(info[0]);++indeg[info[0]];}queue<int> q;// 将所有入度为 0 的节点放入队列中for (int i = 0; i < numCourses; ++i) {if (indeg[i] == 0) {q.push(i);}}while (!q.empty()) {// 从队首取出一个节点int u = q.front();q.pop();// 放入答案中result.push_back(u);for (int v: edges[u]) {--indeg[v];// 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了if (indeg[v] == 0) {q.push(v);}}}if (result.size() != numCourses) {return {};}return result;}
};

lc684.冗余连接–中等

题目描述

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

img

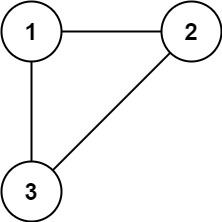
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

img

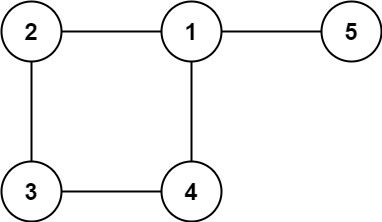
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ai < bi <= edges.length
  • ai != bi
  • edges 中无重复元素
  • 给定的图是连通的

代码展示

class Solution {
public:        //并查集int Find(vector<int>& parent, int index) {if (parent[index] != index) {parent[index] = Find(parent, parent[index]);}return parent[index];}void Union(vector<int>& parent, int index1, int index2) {parent[Find(parent, index1)] = Find(parent, index2);}vector<int> findRedundantConnection(vector<vector<int>>& edges) {int n = edges.size();vector<int> parent(n + 1);for (int i = 1; i <= n; ++i) {parent[i] = i;}for (auto& edge: edges) {int node1 = edge[0], node2 = edge[1];if (Find(parent, node1) != Find(parent, node2)) {Union(parent, node1, node2);} else {return edge;}}return vector<int>{};}
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/150160.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

我的第一个react.js 的router工程

我的第一个react.js 的router工程

react.js 开发的时候&#xff0c;都是针对一个页面的&#xff0c;多个页面就要用Router了&#xff0c;本文介绍我在vscode 下的第一个router 工程。 我在学习react.js 前端开发&#xff0c;学到router 路由的时候有点犯难了。经过1-2天的努力&#xff0c;终于完成了第一个工程…
阅读更多...
【安鸾靶场】实战渗透

【安鸾靶场】实战渗透

文章目录 前言一、租房网 (150分)二、企业网站 (300分)三、SQL注入进阶 (550分) 前言 最近看到安鸾的靶场有些比较有意思就打了一下午&#xff0c;有一定难度。 一、租房网 (150分) http://106.15.50.112:8031/ 刚打开burp就报了thinkphp的代码执行 直接getshell flag&a…
阅读更多...
【Docker】Docker的应用包含Sandbox、PaaS、Open Solution以及IT运维概念的详细讲解

【Docker】Docker的应用包含Sandbox、PaaS、Open Solution以及IT运维概念的详细讲解

前言 Docker 是一个开源的应用容器引擎&#xff0c;让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 &#x1f4d5;作者简介&#xff1a;热…
阅读更多...
【数据结构】栈的实现

【数据结构】栈的实现

&#x1f6a9;纸上得来终觉浅&#xff0c; 绝知此事要躬行。 &#x1f31f;主页&#xff1a;June-Frost &#x1f680;专栏&#xff1a;数据结构 &#x1f525;该文章主要了解实现栈的相关操作。 目录&#xff1a; &#x1f30d; 栈的概念&#x1f30e;栈的实现✉️ 初始化栈 和…
阅读更多...
Linux-centos系统安装MySql5.7

Linux-centos系统安装MySql5.7

1.配置yum仓库 1.1配置yum仓库 rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2022 1.2 安装Mysql yum库 rpm -Uvh http://repo.mysql.com//mysql57-community-release-el7-7.noarch.rpm 2.使用yum安装Msql 说明&#xff1a;下载大约5分钟左右 yum -y install mysq…
阅读更多...
【赠书活动】Excel透视表的简单应用

【赠书活动】Excel透视表的简单应用

&#x1f449;博__主&#x1f448;&#xff1a;米码收割机 &#x1f449;技__能&#x1f448;&#xff1a;C/Python语言 &#x1f449;公众号&#x1f448;&#xff1a;测试开发自动化【获取源码商业合作】 &#x1f449;荣__誉&#x1f448;&#xff1a;阿里云博客专家博主、5…
阅读更多...
如何优雅构建自定义 Spring Boot 验证器，让你的代码更加丝滑！

如何优雅构建自定义 Spring Boot 验证器，让你的代码更加丝滑！

作为一名开发人员&#xff0c;你应该知道确保应用程序中流动的数据的准确性和完整性是多么重要。Spring Boot提供了强大的验证功能&#xff0c;但有时我们需要额外的验证&#xff0c;创建适合特定需求的自定义验证器。 接下来&#xff0c;我们来介绍下如何完整的创建一个自定义…
阅读更多...
日期相关工具类

日期相关工具类

日期相关工具类 【一】介绍【1】SimpleDateFormat 为什么是线程不安全【2】解决 SimpleDateFormat 线程不安全的方法 【二】LocalDate API【三】LocalTime API【四】LocalDateTime API【五】转换关系【1】LocalDateTime 与 LocalDate 之间的转换【2】LocalDateTime 与 Date 之间…
阅读更多...
账户和组管理

账户和组管理

1. 账户和工作组的分类 1.1. 用户分为三类&#xff1a; 超级账户——账户名为root&#xff0c;它具有一切权限&#xff0c;只有进行系统维护(例如&#xff1a;建立用户等)或其他必要情形下才 用超级用户登录&#xff0c;以避免系统出现安全问题。 系统账户——是Linux系统正常…
阅读更多...
软件工程与计算总结（四）项目管理基础

软件工程与计算总结（四）项目管理基础

目录 一.项目和项目管理 二.团队组织与管理 三.软件质量保障 四.软件配置管理 五.项目实践 一.项目和项目管理 1.软件开发远不是纯粹的编程&#xff0c;随着软件规模的增长&#xff0c;软件开发活动也变得越来越复杂~ 2.软件项目就是要将所有的软件开发活动组织起来&#…
阅读更多...
简单聊一聊公平锁和非公平锁，parallel并行流

简单聊一聊公平锁和非公平锁，parallel并行流

目录 一、降低锁的粒度&#xff0c;将synchronized关键字不放在方法上了&#xff0c;改为synchronized代码块。二、先区分一下公平锁和非公平锁1、公平锁2、非公平锁3、公平锁的优缺点&#xff1a;4、非公平锁的优缺点&#xff1a; 三、是否对症下药四、IntStream.rangeClosed是…
阅读更多...
【问题解决】报错：unable to execute ‘swig‘: No such file or directory

【问题解决】报错：unable to execute ‘swig‘: No such file or directory

在编译uboot代码时&#xff0c; make -f rockpi4.mk u-boot -j4 报了以下错误。 HOSTCC scripts/dtc/dtc.oSHIPPED scripts/dtc/pylibfdt/libfdt.iENVT include/generated/environment.hPYMOD rebuildHOSTCC scripts/dtc/flattree.oUPD include/generated/version_…
阅读更多...
【手绘 | 日漫风】从临摹开始控笔，线条，再到人体

【手绘 | 日漫风】从临摹开始控笔，线条，再到人体

博主&#xff1a;_LJaXi 专栏&#xff1a; Unity | 横版游戏开发 手绘入门 控笔 排线起稿方式九宫格起稿五官起稿专业起稿 握笔姿势三角握持姿势拇指指握姿势 勾线建议注意对于人体 控笔 排线 在绘画过程中&#xff0c;可以使用铅笔控制笔触的方向、压力和角度&#xff0c;以获…
阅读更多...
力扣 -- 446. 等差数列划分 II - 子序列

力扣 -- 446. 等差数列划分 II - 子序列

解题步骤&#xff1a; 参考代码&#xff1a; class Solution { public:int numberOfArithmeticSlices(vector<int>& nums) {int nnums.size();//把元素和它对应的所有下标绑定存放到哈希表中unordered_map<double,vector<int>> hash;for(int i0;i<n;…
阅读更多...
picodet onnx转其它芯片支持格式时遇到

picodet onnx转其它芯片支持格式时遇到

文章目录 报错信息解决方法两模型精度对比 报错信息 报错信息为&#xff1a; Upsample(resize) Resize_0 not support attribute coordinate_transformation_mode:half_pixel. 解决方法 整个模型转换过程是&#xff1a;paddle 动态模型转成静态&#xff0c;再用paddle2onnx…
阅读更多...
网站安全维护：守护您的数字领土

网站安全维护：守护您的数字领土

在这个数字时代&#xff0c;网站已成为企业和个人展示自己的重要平台。然而&#xff0c;随着互联网的高速发展&#xff0c;网站安全问题也日益严峻。黑客和入侵软件等威胁不断涌现&#xff0c;因此&#xff0c;保护网站免受这些威胁的影响变得至关重要。本文将探讨网站安全维护…
阅读更多...
字符串常量池位于JVM哪里

字符串常量池位于JVM哪里

Java6 和6之前&#xff0c;常量池是存放在方法区&#xff08;永久代&#xff09;中的。Java7&#xff0c;将常量池是存放到了堆中。Java8 之后&#xff0c;取消了整个永久代区域&#xff0c;取而代之的是元空间。运行时常量池和静态常量池存放在元空间中&#xff0c;而字符串常…
阅读更多...
【软件测试】功能测试/接口测试/自动化测试/性能测试/验收测试

【软件测试】功能测试/接口测试/自动化测试/性能测试/验收测试

软件测试的主要流程 一、测试主要的四个阶段 1.测试计划设计阶段&#xff1a;产品立项之后&#xff0c;进行需求分析&#xff0c;需求评审&#xff0c;业务需求评级&#xff0c;绘制业务流程图。确定测试负责人&#xff0c;开始制定测试计划&#xff1b; 2.测试准备阶段&…
阅读更多...
【STM32单片机】多功能电子密码锁设计

【STM32单片机】多功能电子密码锁设计

文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用STM32F103C8T6单片机控制器&#xff0c;使用按键、IIC OLED模块、DS18B20温度传感器、SG90舵机、红外遥控、矩阵按键、EEPROM等。 主要功能&#xff1a; 系统运行后&#xff0c;OLED显示RTC日期…
阅读更多...
【C++面向对象侯捷下】21. 关于New， Delete

【C++面向对象侯捷下】21. 关于New， Delete

文章目录 底层 是 调用 malloc函数 class 可以 重载这些 函数&#xff08;可以重载 构造&#xff0c;析构函数&#xff1f;&#xff09;
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023

友情链接： 我的编程经验分享 一条长河网 尧图网站开发