W...Y的主页 😊
代码仓库分享 💕

🍔前言:
上篇博客我们讲解了非常重要的快速排序,相信大家已经学会了。最后我们再学习一种特殊的排序手法——归并排序。话不多说我们直接上菜。
目录
归并排序
基本思想
递归思路
算法思路
代码思路以及实现
非递归思路
算法思路编辑
代码思路以及实现
归并排序的特性总结
非比较排序
计数排序
算法思路以及代码实现
计数排序总结
八大排序总结
归并排序
基本思想
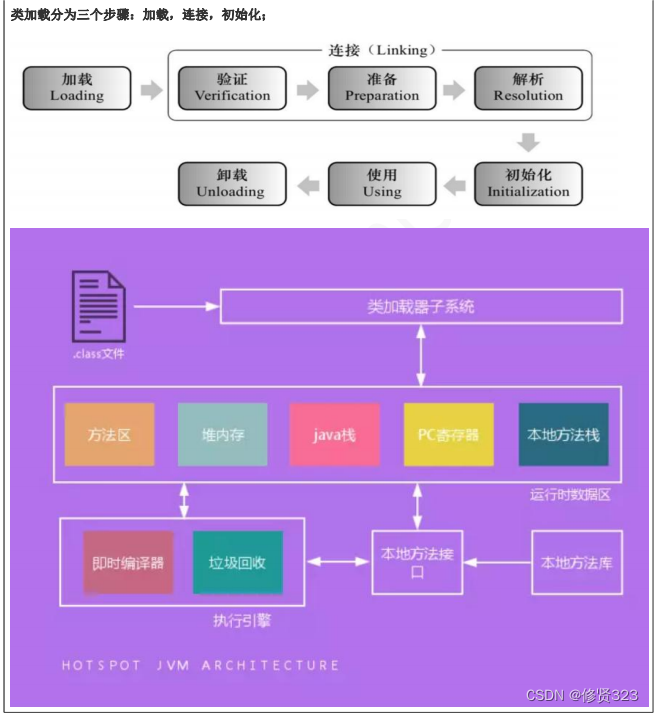
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
递归思路
算法思路
归并排序的思路就是先分再合。
1.我们将一个数组进行平分,然后继续递归进行更细小的划分秒,直到每个数组如同一个数组时,然后再进行返回。
2.返回时每个小数组中的数必须排列为有序的数。
3.然后合并每个小数组,然后继续进行排序直到数组有序即可。
我们可以展示一下归并排序的动图,让大家更好的理解:

代码思路以及实现
不难看出递归的过程非常像二叉树的后序遍历数组,如果左右区间都无序,我们进行向下递归,直到有序再返回合并。(只有一个数时,我们可以看作其有序)
所以我们的代码思路也与二叉树后序代码有点相似。
具体思路:
1.创建一个与原数组相同空间大小的数组用来拷贝已经排序好的子数组。
2.创建一个函数来进行递归调用,如果使用有malloc的函数,递归时会重复开辟空间导致空间浪费,函数的参数传入原数组,新建数组与排序的起始位置与终止位置。
3.进行数组的递归调用。
4.创建临时遍历begin1、end1、begin2、end2,控制子数组的区间,然后进行比较排序成为有序子数组。
5.将有序的数组先放入新数组中,然后拷贝到原数组中进行覆盖,变为有序数组即可。
代码实现:
void _MergeSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (end + begin) / 2;//[begin, min][min + 1, end]_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid + 1, end);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, tmp, 0, n - 1);free(tmp);
}
易错点:
在拷贝时,我们不一定是从头进行拷贝,拷贝的都是与数组头的相对位置,所以在参数中我们要添加begin。
非递归思路
为什么要进行非递归,与快速排序的原因相同,就是因为递归占用的是栈空间,而栈空间的内存非常小,所以我们要进行非递归的算法学习。而非递归与斐波那契切数的思路相当,就是已知前两个然后去推后面的数,而归并的非递归也是如此,将思路进行正向整理,从最小的开始进行即可。
算法思路

我们先创建一个gap数进行子数组大小记录,gap为1则进行一一比较排序,gap = 2则进行两个两个比较以此类推。后面与递归思路基本相同。
代码思路以及实现
实现思路:
1.模拟递归最后一层进行比较排序。
2.每次gap *= 2.
3.当gap>=n时停止递归。
4.将有序数组进行拷贝
代码实现:
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int*) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = i;if (begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}printf("[%d][%d][%d][%d] ", begin1, end1, begin2, end2);while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}printf("\n");gap *= 2;}free(tmp);
} 注意:当我们进行排序时,我们就会进行分组。但是有些数组中的元素个数不一定够组成一组。当我们一个一个进行分组时,我们可以将所以元素分为一组,但是当个数为奇数时,我们进行归并后进行两个一组时,就会有一个剩余。四个进行分组时也会有其中一组或两组没有分满的情况,所以我们如果不进行控制,就会出现数组越界的情况,程序就会报错。
我们将每一次的递归区间进行打印即可看出区间越界的问题:
 但是我们进行修改后就不会出现越界情况:
但是我们进行修改后就不会出现越界情况:

其中越界的有end2、begin2、end1。begin1是不会越界的。那我们将其进行边界的修正,这样即不会影响正常的归并,也不会将出错的情况算入其中。
处理方法:
如果end2越界,则将其修改为n-1。
如果begin2和end1越界,则将其修正为不存在的区间,不存在则直接跳出了归并的过程。
共用三种出界情况.
但是如果begin2越界或end1越界程序直接break即可,其实直接写begin2就可以涵盖所有情况,所以我们可以将begin1>n省略。
归并排序的特性总结
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
非比较排序
非比较排序的思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
计数排序
计数排序是一种比较新奇的排序思路,它没有两两数之间的比较,而是统计每个数出现的次数,然后进行排序。
这种方法适合于数目比较集中的情况,且整型数据。
时间复杂度:O(N + range) 空间复杂度:O(range)
算法思路以及代码实现
思路:
1.先寻找数组中出现的最大数与最小数。
2.开辟最大数-最小数差值的数组空间大小
3.遍历数组,统计数组中每个数出现的次数放入开辟好的数组中去。
4.遍历新建数组中的内容,每个数出现几次,就在旧数组中打印几次,覆盖掉原数组的内容。
代码实现:
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (size_t i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);printf("range:%d\n", range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);// 统计数据出现次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}注意:我们统计的数组不一定从0开始,所以我们在统计出数组中的最小值时一定要在默认在每个下标后加最小值才可以得到原数组中的内容。
计数排序总结
计数排序的特性总结:
1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
2. 时间复杂度:O(MAX(N,范围))
3. 空间复杂度:O(范围)
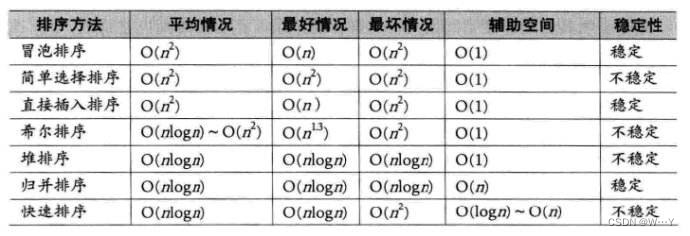
八大排序总结
总结:几种常见易错且重要的排序在这里就讲述完了,我们要合理引用,发挥出排序的优点,舍弃其缺点。最后我将这些排序的复杂度以及稳定性进行了总结,我们可以适度观看。 
以上就是本次博客全部内容,感谢大家观看!!!

![[NewStarCTF 2023 公开赛道] week1](https://img-blog.csdnimg.cn/b0f1e58f85c44a90a94e95d36bd2945c.png)

![【QT5-程序控制电源-[GPIB-USB-HS]-SCPI协议-上位机-基础样例【2】】](https://img-blog.csdnimg.cn/b8cbae930c5e4fa3aa611470c05809d8.png)