给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

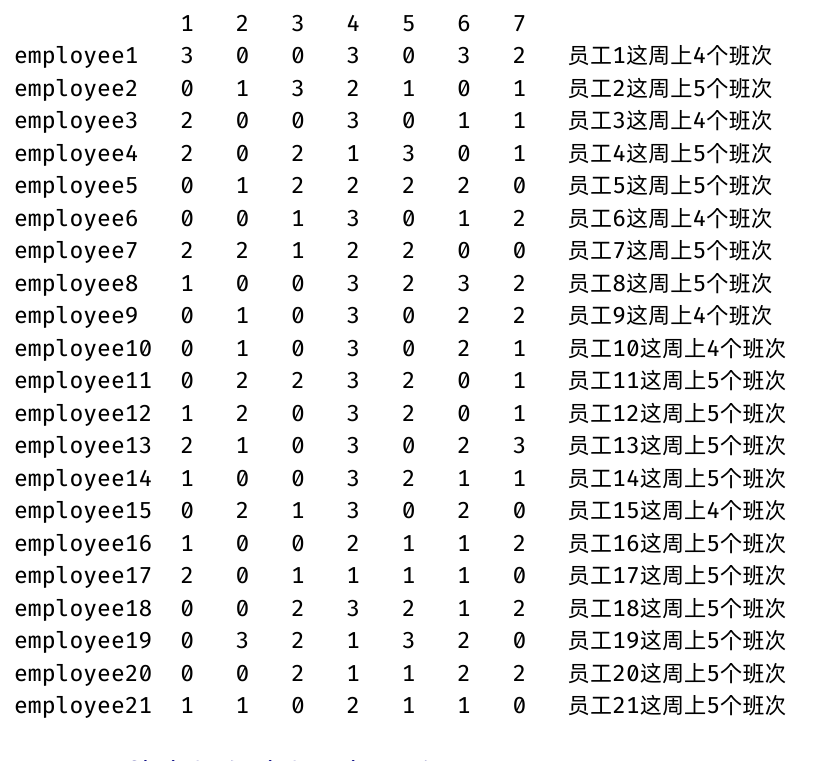
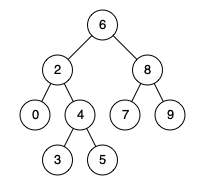
例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

 //本题，由于是找到 == q，p的parent，所以找到就返回，而不用遍历整棵树，所以，采用return

。递归函数有返回值，那就是搜索一条边，符合就立即返回。但是有返回值（搜索一条边），也要看，是搜索一条边还是整棵树。很明显二叉搜索树，不需要搜索整棵树。而二叉树需要搜索整棵树，因为没有二叉搜索树的特性，导致需要右子树的返回值做判断。

class Solution {
public:TreeNode* dfs(TreeNode* root,TreeNode* p,TreeNode* q){if(!root) return root;//中序if(root->val > p->val && root->val > q->val){TreeNode* left = NULL;left = dfs(root->left,p,q);if(left) return left;}else if(root->val < p->val && root->val < q->val){ TreeNode* right = NULL;right = dfs(root->right,p,q);if(right) return right; //由于是找到符合的值就返回，所以是遍历一条边，而不是整棵树}return root;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//dfsif(!root) return root; return dfs(root,p,q);}
};

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//迭代TreeNode* cur = root;while(cur){if(cur->val < q->val && cur->val < p->val){cur = cur->right;}else if(cur->val > q->val && cur->val > p->val){cur = cur->left;}else{return cur;}}return cur;}
};