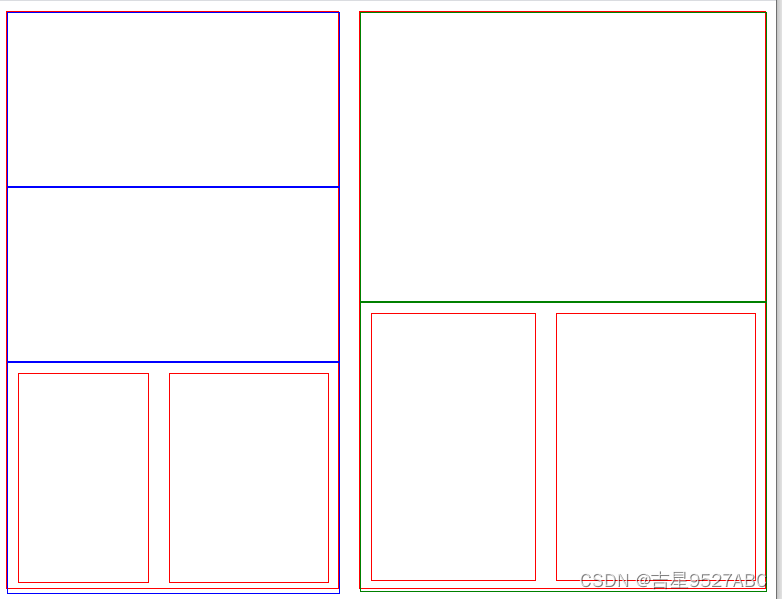
队列安排1160

灵活的插入与删除

用队列实现的话，就是双端队列，

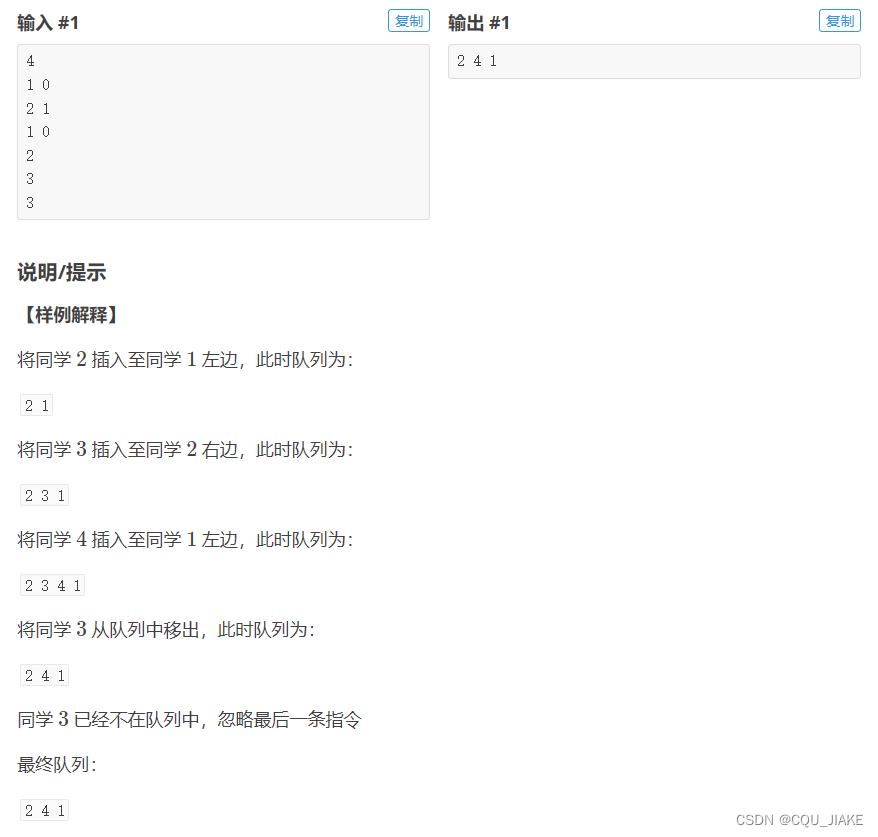
第一阶段是要找到对应编号的同学，然后根据p的取值决定是怎么插入

第二阶段也是要找到对应编号同学，之后就删除，如果找不到就返回

思路是这个思路，可以用数组来实现，第一阶段不变，第二阶段可以优化为，如果输入了对应的编号，就让那个编号的同学不输出，最后在统一遍历输出时，就只会输出那些没有被打上标记的人

？既然用数组实现，怎么能按逻辑顺序遍历？

可以用一个数组0号元素，它的右侧就是第一个元素，遍历的终点是右侧遇到了0 

    cha(1, 0, 1);for (int i = num[0].r; i != 0; i = num[i].r) {if (num[i].flag == 1) {cout << i << " ";}}

这一段是精髓 

    struct peo {int l, r;int flag = 1;}num[10005];void cha(int i, int k, int p) {//k是被插的，i是新来的if (p == 1) {//i插在k的右边num[i].r = num[k].r;num[i].l = k;num[k].r = i;num[num[i].r].l = i;}else if (p == 0) {num[i].l = num[k].l;num[i].r = k;num[k].l = i;num[num[i].l].r = i;}}int n, k, p, m, x;cin >> n;cha(1, 0, 1);for (int i = 2; i <= n; i++) {cin >> k >> p;cha(i, k, p);}cin >> m;for (int i = 1; i <= m; i++) {cin >> x;num[x].flag = 0;}for (int i = num[0].r; i != 0; i = num[i].r) {if (num[i].flag == 1) {cout << i << " ";}}

机器翻译1540（队列）

感觉和滑动窗口差不多

用一个长度为m的窗口去滑动n的长度，如果n<m直接返回n，

考虑到前m个可能有重复的情况，用左右指针，不好用，还是队列

然后往后遇到数字时，如果前面记录过这个数字就接着走，如果没有，就让队头出队，然后这个元素入队，并且cnt++,最后输出cnt，即入队时cnt++,一旦到了内存，就一直会是满内存的状态

？问题关键在于怎么检索是否遇到这个数字，总不能每次都从头到尾，那就是nm的复杂度？

思想是队列的思想，实现还是用数组更优。用两个数组，一个数组a模拟当前内存，一个数组b模拟当前内存中存入的单词情况，遇到元素时，查找b数组上记录的值是否为1，是1就遇到过，直接向后，是0就是没遇到过，要入队，同时在b里置为1，表示现在遇到了，同时如果满内存了，就要让最先遇到的元素的b再置为0

就是遇到有的单词时，如果内存里有，就都不动，接着向后移动

遇到新单词时，就让a数组的第一个元素去掉（用左指针实现，为左指针右移一个单位）

？用两个数组，怎么确定当前的内存长度？

a数组的左右指针，右指针只有在遇到新单词时才会移动，并修改内存，内存也是如此，而一旦到了内存的最大，就会一直是最大，不会往下掉

？既然删除，怎么处理模拟数组中的相同元素，删除首个元素后，如果后面都是这个元素，那怎么找到第二个遇到的不同的元素？

a数组只记录不重复元素，

因为模拟的内存，只有在遇到新元素时才会扩大内存或修改内存，如果一直遇到相同元素，那么内存就会一直不变，就是可以理解内存为记录不同的单词的数量，其最多为m,而不是实际的长度

这样左指针右移时遇到的就一定不是相同的元素，而是下一个最近的不同单词

改错：前置后置的思考 

#include <iostream>
#include <stdio.h>
#include <algorithm>
using namespace std;
int n, m, x, ans = 0, l = 0, r = 0, a[1005], b[1005];
int main()
{cin >> m >> n;l = 0; r = 0;//初始化两个指针for (int i = 1; i <= n; i++) {cin >> x;if (b[x] == 0) {//内存中没有，要查找a[r++] = x;ans++;b[x] = 1;if (r > m - 1) {b[a[l++]] = 0;}}}cout << ans;return 0;
}

这样写有问题，因为如果内存为1时，会输出5，因为m-1=0,会一直右移左指针

问题不出在前置或者后置++，而在于r>m-1,应该就是r>m,无论是前置还是后置

之前想的是如果后置，那就是让数组第一位存数时，那么此时r就代表内存大小，事实也是如此，因为r=1时，就代表有一个单词，r=2就代表有两个单词，只不过是从0开始记录

如果前置，就是从i=1开始计数，r=1时有一个数

只不过前置时，每次结束时右指针指向的是有值的，后置时，右指针指向的是没值，但实际上指向的位置是同一个位置，因为前置就是从1开始记录，后置就是从0开始记录，相当于往前推了一点

也就是说无论前置后置，遇到两个新数，那么前置后置结果都是r=2, 所以r代表的就是长度，和前置后置无关，只是记录的数据位置不同，最后的数都是一样的

表达式转换1175（栈，中缀转后缀，并模拟计算过程，辅助栈应用，正逆序）

它是要转化为字符串

？计算前中后的结果简单，但怎么由中缀转为后缀表达式的字符串？

不改变数字出现的相对顺序，改变的只是符号的出现顺序

？怎么改变符号的出现顺序，规则是？

定义优先级，如果此时符号栈中的栈顶元素优先级比自己高，那就让栈顶元素出来，表示先让程序算它，知道遇到优先级不比自己高的

如果比自己优先级低或相等，就直接入栈，这样在算的时候也是先算自己这个优先级比栈下面都更高的操作符，如果都相等，就是遵循从右到左的运算顺序

不对，应该出的是所有大于等于自己优先级的，不是从右到左，对加和乘没区别，但是对减和除有区别，就应该是从左到右，所以应该是出掉所有优先级大于等于自己的，让栈里的下个元素是优先级比自己小的

括号不参与比较，括号只是起隔绝的作用

？遇到括号怎么处理？

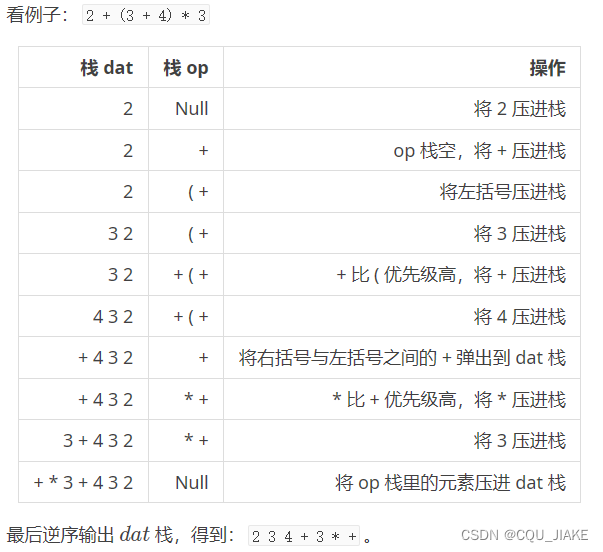
遇到括号时就是同样入栈，先遇到左括号，后遇到右括号，在遇到右括号时，就要在符号栈里依次出元素，知道遇到左括号结束，左右括号不输出 

括号不参与优先级比较，遇到括号就直接进，知道遇到右括号才出

第一问解决 

//输入，并演示一步一步的转变过程
//先是输入一个原始字符串，然后转为后缀表达式
//转为原始的后缀表达式后，就开始模拟计算，每行一步
//就是遇到数字就进栈，然后遇到第一个符号就出栈两个，算完入栈一个，接着继续入栈后续的原栈元素，最后再输出
//直到只有一个元素string s;int p(char s) {switch (s) {case '+':return 1;case '-':return 1;case '*':return 2;case '/':return 2;case '^':return 3;default:return -1;}}bool flag = 1;stack<char>op;stack<char>str;void change(string s) {for (int i = 0; i < s.size(); i++) {if (s[i] == ' ') { continue; }if (isdigit(s[i])) {str.push(s[i]);}//遇到数字else if (s[i] == '(') {op.push('(');}//特判遇到左括号else {//遇到操作符if (s[i] == ')') {while (op.top() != '(') {str.push(op.top());op.pop();}op.pop();//此时出循环后栈顶元素为左括号，出掉}else {while (!op.empty() && p(op.top()) >= p(s[i])) {//只要栈顶的元素优先级比自己高，就让它先出去，直到遇到同优先级，遵循从右到左计算str.push(op.top());//这里出问题是因为op里有左括号，但是它却返回不出来一个数,然后就会报错op.pop();}op.push(s[i]);}}}while (!op.empty()) {str.push(op.top());op.pop();}//最后要把遗留在符号栈里的操作符都移出来//这个函数是用来把中缀表达式转变为后缀表达式}cin >> s;//while (s.size()) {change(s);s = "";while (!str.empty()) {s += str.top();s += " ";str.pop();}reverse(s.begin(), s.end());cout << s << endl;while (s.size()) {//接下来就是不断遇到两个数，和一个操作符后进行计算，使s的长度不断减小，最后只剩下一个字符，即最后结果}// }

 完整版

怎么输出是重点，每行怎么输出，怎么保证顺序的一致，辅助栈的应用，栈之间的来回倒

需要确定哪个栈里是正序，

输出的时候要正序的栈

stack<char>dat, op;
stack<int>num, dat2;
int p(char c) {switch (c) {case'+':return 1;case'-':return 1;case'*':return 2;case'/':return 2;case'^':return 3;default:return -1;}
}
void change(string s) {for (int i = 0; i < s.size(); i++) {if (isdigit(s[i])) {dat.push(s[i]);}else if (s[i] == '(') {op.push(s[i]);}else {if (s[i] == ')') {while (op.top() != '(') {dat.push(op.top());op.pop();}op.pop();}else {if (!op.empty()) {while (!op.empty() && p(s[i]) <= p(op.top())) {//这样主要是考虑到减法和除法的次序问题if (p(s[i]) == p(op.top()) && s[i] == '^') {//但相等时如果是幂运算，其不需要考虑，一方面是因为为最高级，另一方面因为需要考虑次序问题//但连起来的幂运算和连起来的减除运算方向不同，对减除是从左到右，即被减数减减数//幂运算是要从右到左，即把幂上幂上幂……转为幂上一个数,即是需要同运算级从右向左运算的，所以不需要移出来先算，而是最后计算时让其模拟中缀的从右往左算break;//直接退出，不必再做条件判断}else {dat.push(op.top());op.pop();}}}op.push(s[i]);}}}while (!op.empty()) {dat.push(op.top());op.pop();}while (!dat.empty()) {op.push(dat.top());dat.pop();}//利用两个栈完成一次对栈空间元素的倒置输出while (!op.empty()) {cout << op.top() << " ";dat.push(op.top());//这个是为了保存当前的数据，不然的话打印一个必须要删除一个才能打印下一个，就不能完成后续的操作了op.pop();//此时dat直接输出是逆序的，即第一个数最后一个输出}cout << endl;
}

第二问，输出的格式化 

int jisuan(int x, int y, char t) {switch (t) {case'+':return x + y;case'-':return x - y;case'*':return x * y;case'/':return x / y;case'^':return pow(x, y);}
}
void cal() {while(!dat.empty()){op.push(dat.top());dat.pop();//}//再倒回去，目的是为了得到正序，从而模拟计算//即此时op里的数是正序的，第一个数第一个输出，但是又进了Num栈，这就导致第一个访问到的不是最早的数//而是最新入num栈的数，即被减数减数的关系中，op栈里是被减数在上面，先输出，是正序的//而从op栈转到Num栈里，就变成了被减数在下面，减数在上面，此时直接运算，就是逆序，是错误的，所以在计算时需要注意while (!op.empty()) {if (isdigit(op.top())) {num.push(op.top() - '0');op.pop();}else {//遇到操作符的必要条件就是已经遇到了至少两个操作数，即可以肯定在遇到第一个操作符时已经可以进行运算//而目的就是接下来每行只计算一个操作符int x = num.top();num.pop();int y = num.top();num.pop();num.push(jisuan(y, x, op.top()));//这里就完成了本行的任务，就不需要再继续用numop.pop();//此时num是一个逆序状态，可以再倒到一个辅助栈里，使其成为正序，进行一下输出//这里就是接下来每行的输出，在这个方法中其由两部分组成，一部分为从Num倒到辅助栈里后的正序顺序输出//这个可以保证是第一个操作符之前的部分，然后就是op栈里的部分，这是遇到此时剩下的首个操作符之后的其他部分//整个过程，大的循环就是op循环，即不断根据op里剩下的首个操作符位置划分的过程//每op循环一次，就是一行的结束，当op里没元素时，就没有了操作符，计算结果也进入了num数组，输出就可以了while (!num.empty()) {//这个辅助栈必须和Num同类型，都为int型dat2.push(num.top());num.pop();}while (!dat2.empty()) {cout << dat2.top() << " ";num.push(dat2.top());//由于已经从字符转为整数型，所以应再倒回num栈里，以进行下个Op循环dat2.pop();}//两部分，一部分是首个操作符之前的，另一部分是其之后的while (!op.empty()) {cout << op.top() << " ";dat.push(op.top());op.pop();}//是为了输出op剩下的部分，由于op此时已经是正序，所以直接输出即可，但是为了保存，还需要用到辅助栈dat,char类型的，最后还要再复原回去while (!dat.empty()) {op.push(dat.top());dat.pop()}cout << endl;//标志着本次op循环的结束}}
}
string s;
cin >> s;
change(s);
cal();