题目列表

2869. 收集元素的最少操作次数

2870. 使数组为空的最少操作次数

2871. 将数组分割成最多数目的子数组

2872. 可以被 K 整除连通块的最大数目

一、收集元素的最小操作次数

直接模拟，倒序遍历即可，代码如下

class Solution {
public:int minOperations(vector<int>& nums, int k) {set<int>cnt;int n=nums.size();for(int i=n-1;i>=0;i--){if(nums[i]<=k) cnt.insert(nums[i]);if(cnt.size()==k) return n-i;}return n;}
};//由于数据范围比较小，这里可以用位运算将空间复杂度将为O(1)
class Solution {
public:int minOperations(vector<int>& nums, int k) {long long s=(1LL<<(k+1))-1-1;//每个二进制位，0代表没有出现，1代表出现long long x=0;int n=nums.size();for(int i=n-1;i>=0;i--){if(nums[i]<=k) x|=(1LL<<nums[i]);if(x==s) return n-i;}return n;}
};

 二、使数组为空的最小操作次数

这题只要发现规律也不是很难，根据题目意思我们需要统计每个数出现的次数，然后得到每个元素被删除的最小操作次数，相加得到答案，难点在于获取每种元素被删除的最小操作次数。

其实这题的本质就是看一个数可以由多少个2和多少个3组成，并且2的个数加3的个数要最少，如果你数学好，这题就已经被秒了，如果你数学不好，那咋们就来举几个例子，找找规律

 代码如下

class Solution {
public:int minOperations(vector<int>& nums) {int ans=0;unordered_map<int,int>cnt;for(int x:nums)cnt[x]++;for(auto&[_,c]:cnt){if(c==1) return -1;ans+=(c+2)/3;}return ans;}
};

 三、将数组分割成最多数目的子数组

这题主要是了解按位与的性质---只有同为1，按位与后才是1，所以按位与的数字越多只会让数变得越来越小，这题要求子数组按位与之和要尽可能的小， 根据性质，所有数字按位与后的值才是最小的(设为a)，如果将数组拆分成n个子数组，每个子数组按位与后的结果为bi(2<=i<=n)，且bi>=a，所以sum(bi)>a，所以答案返回1，对吗？

别忘了一种特殊情况，如果a=bi=0呢？这时我们就能对数组进行拆分了，根据贪心，每当我们遇到一段区间的按位与和为0，我们就将子数组个数+1，最后返回答案

代码如下

class Solution {
public:int maxSubarrays(vector<int>& nums) {int ans=0;int s=-1;//-1的二进制位为全1,不会对按位与运算产生任何影响for(int i=0;i<nums.size();i++){s&=nums[i];if(s==0){ans++;s=-1;}}return max(ans,1);}
};

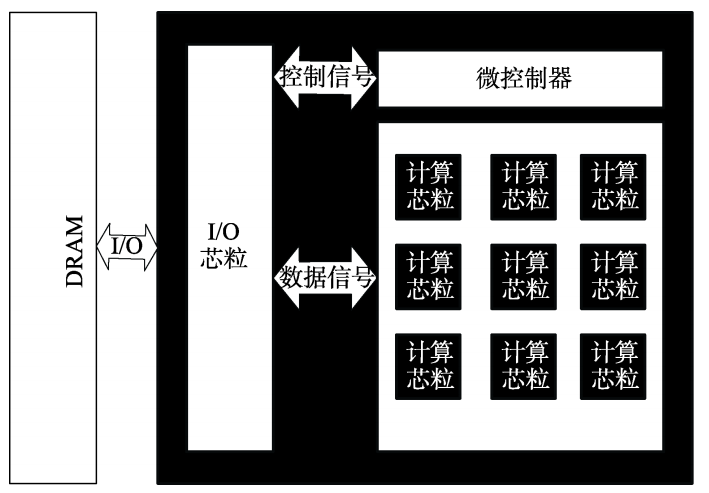
四、可以被k整除的连通块的最大数目

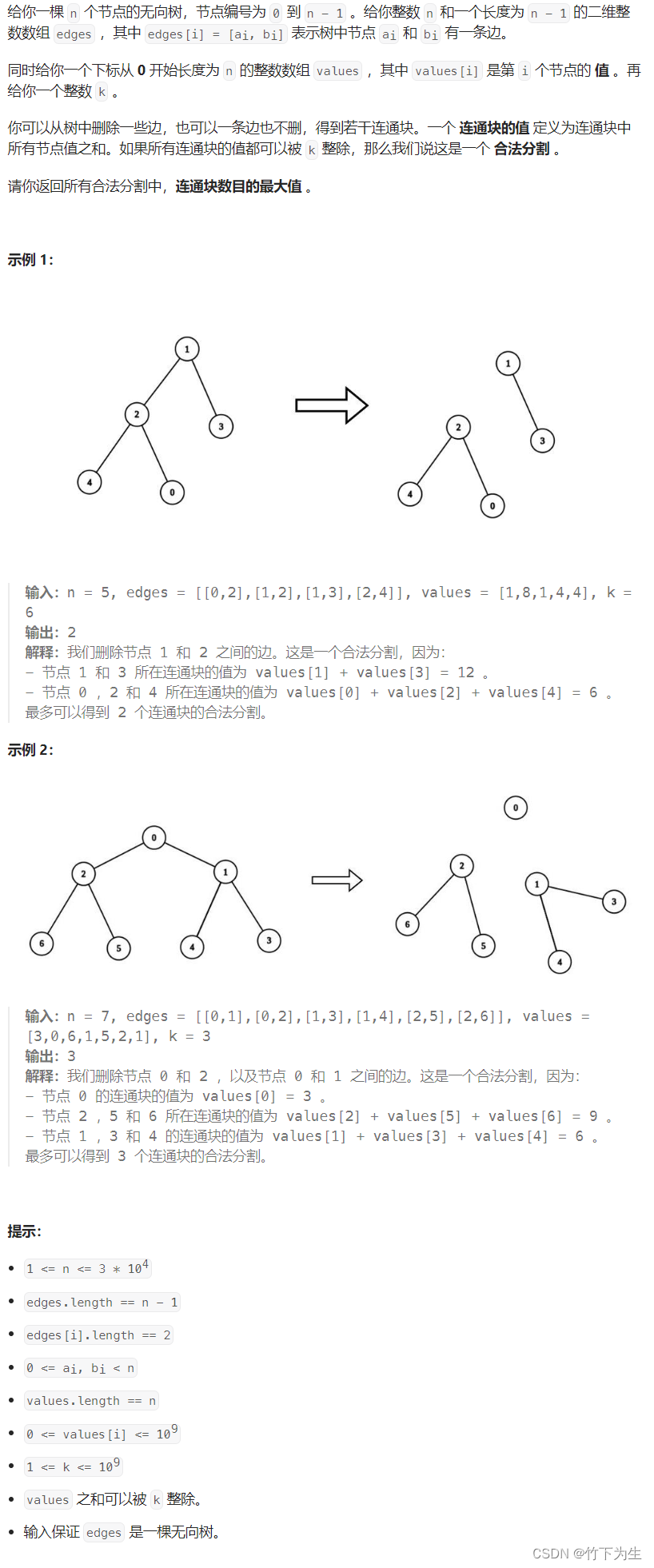
这题找能否被k整除的连通块的个数，我们先计算每个连通块的值，只要连通块的值能被k整除，答案就+1(因为k的倍数减去k的倍数的结果还是k的倍数)，代码如下

class Solution {
public:typedef long long LL;int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {vector<vector<int>>g(n);for(auto&e:edges){int x=e[0],y=e[1];g[x].push_back(y);            g[y].push_back(x);}//计算以每一个结点为根的连通块的值int ans=0;function<LL(int,int)>dfs=[&](int x,int fa)->LL{LL v=values[x];for(auto& y:g[x]){if(y!=fa){v+=dfs(y,x);}}if(v%k==0) ans++;return v;};dfs(0,-1);return ans;}
};