切面条

一根高筋拉面，中间切一刀，可以得到2根面条。

如果先对折1次，中间切一刀，可以得到3根面条。

如果连续对折2次，中间切一刀，可以得到5根面条。

那么，连续对折10次，中间切一刀，会得到多少面条呢？

解题

这就是最容易想到的，找数字之间的规律，如前三次的切面条，分别对折0次，1次，2次，分别得到的面条根数是2，3，5，你可能会画出对折3次的面条来继续验证，如图

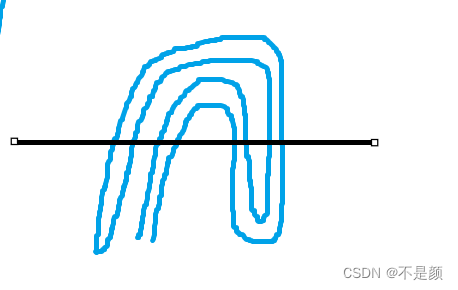
原谅我的画功有限，的的确确是9根，但是可以看出：面条根数 = 2的面条的对折次数次方 + 1 ；可是我觉得这不太严谨。（要想画出对折4次的面条来验证较为困难）

所以还需要一种更为清楚明白的图，如图

分别为对折0，1，2，3次的图，第一次的弯折为0个，第二次的弯折为1个，第三次的弯折为2个（不包括下面的弯折），第三次的弯折为4个（不包括下面的弯折），每对折一次弯折的个数 * 2，如果你把多出来的两根线条连起来，就会发现切割线上的弯折和切割线下的弯折的个数相同。所以有着规律，不必多说。

------------------------------------------------

这个解法是我从讨论区看到的，我觉得和刚刚说的有点类似。

现在有一根线，每次从中间对折，如图：

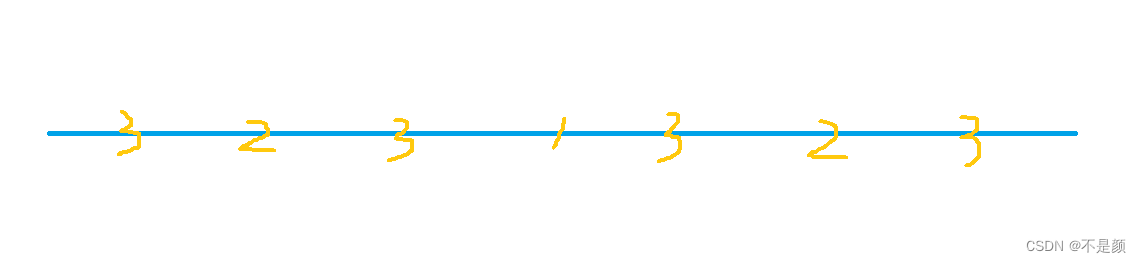
数字代表着第几次对折所产生的折痕。将每一个数字以及两端都认为是截点，先假设1这个截点不存在，每次对折时每两个相邻截点增加一个截点，故：截点的个数 = 2 ^ （对折的次数）

那么计算实际的截点数只需要 + 1 （数字1代表的截点）即可。例如对折十次：2 ^ 10 + 1