Python库学习(九):Numpy[续篇三]:数组运算

NumPy是用于数值计算的强大工具，提供了许多数组运算和数学函数，允许你执行各种操作，包括基本运算、统计计算、线性代数、元素级操作等

1.基本运算

1.1 四则运算

NumPy数组支持基本的四则运算（加法、减法、乘法和除法），它们是元素级别的运算，也称为逐元素运算;

  • numpy.add(): 加法运算,或使用： +;
  • numpy.subtract(): 减法运算，或使用： -;
  • numpy.multiply(): 乘法运算，或使用： *;
  • numpy.divide(): 除法运算，或使用： /; 
import numpy as np

if __name__ == '__main__':
    arr1 = np.array([1, 2, 3, 4])
    arr2 = np.array([10, 20, 30, 40])
    # 加法运算
    print("加法运算(add):", np.add(arr1, arr2))
    print("加法运算(+):", arr1 + arr2)
    # 减法运算
    print("减法运算(subtract):", np.subtract(arr1, arr2))
    print("减法运算(-):", arr1 - arr2)
    # 乘法运算
    print("乘法运算(multiply):", np.multiply(arr1, arr2))
    print("乘法运算(*):", arr1 * arr2)
    # 除法运算
    print("除法运算(divide):", np.divide(arr1, arr2))
    print("除法运算(/):", arr1 / arr2)
    
"""
加法运算(add): [11 22 33 44]
加法运算(+): [11 22 33 44]
减法运算(subtract): [ -9 -18 -27 -36]
减法运算(-): [ -9 -18 -27 -36]
乘法运算(multiply): [ 10  40  90 160]
乘法运算(*): [ 10  40  90 160]
除法运算(divide): [0.1 0.1 0.1 0.1]
除法运算(/): [0.1 0.1 0.1 0.1]
"""    

1.2 平方根

公式说明: 平方根，又叫二次方根，表示为: ; 如 ，那么 4的平方根就是2,表示为: 

import numpy as np

if __name__ == '__main__':
    arr = np.array([1, 4, 9, 16])
    print("一维数组平方根运算:", np.sqrt(arr))
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("二维数组平方根运算:\n", np.sqrt(two_arr))
    
"""
一维数组平方根运算: [1. 2. 3. 4.]
二维数组平方根运算:
 [[1.         1.41421356 1.73205081 2.        ]
 [2.23606798 2.44948974 2.64575131 2.82842712]]
"""    

1.3 幂运算

公式说明: 用于表示一个数（底数）被另一个数（指数）多次相乘的结果,它通常以符号 表示，其中 a 是底数，b 是指数;如: 表示2的立方，计算结果为: 2 * 2 * 2 = 8

import numpy as np

if __name__ == '__main__':
    arr = np.array([1, 2, 3, 4])
    print("一维数组幂运算:\n", np.power(arr, 2))
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("二维数组幂运算:\n", np.power(two_arr, 2))
    
"""
一维数组幂运算:
 [ 1  4  9 16]
二维数组幂运算:
 [[ 1  4  9 16]
 [25 36 49 64]]
"""    

2.统计运算

2.1 求和

np.sum(): 用于计算数组元素总和的函数。它可以接受多个参数，但最常用的是对单个数组进行求和。

import numpy as np

if __name__ == '__main__':
    # 一维数求和运算
    arr = np.array([1, 2, 3, 4])
    print("一维数组求和运算:", np.sum(arr))
    # 二维数组求和运算
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("二维数组求和运算:", np.sum(two_arr))
    # 三维数组求和运算
    three_arr = np.arange(6).reshape((1, 3, 2))
    print("三维数组:\n", three_arr)
    print("三维数组求和运算:", np.sum(three_arr))
    
"""
一维数组求和运算: 10
二维数组求和运算: 36
三维数组:
 [[[0 1]
  [2 3]
  [4 5]]]
三维数组求和运算: 15
"""    

2.2 平均值

np.mean(): 用于计算数组元素平均值的函数。它可以接受多个参数，但最常用的是对单个数组进行平均值计算。

mean(a, axis=None, dtype=None, out=None, keepdims=np._NoValue, *,where=np._NoValue)

a. 参数说明:

  • axis: 可以指定在哪个轴上进行平均值计算。默认情况下，它会对整个数组进行计算，返回一个标量值。
  • dtype: 可以指定结果的数据类型。默认情况下，结果的数据类型与输入数组的数据类型相同。
  • keepdims: 默认情况下,返回一个降维后的数组（标量），但如果设置 keepdims=True，则结果将保持与输入数组相同的维度
  • where: 它接受一个布尔数组或条件表达式，当参数不为空时,将只计算满足条件的元素的平均值，而忽略不满足条件的元素。

b.代码示例:

import numpy as np

if __name__ == '__main__':
    # 一维数组
    one_arr = np.array([10, 20, 30, 40])
    # 二维数组
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("---------------- 不指定参数时 ----------------")
    print("一维数组,求平均值:", np.mean(one_arr))
    print("二维数组,求平均值:", np.mean(two_arr))
    print("---------------- 使用axis参数 ----------------")
    print("二维数组,对列求平均值:", np.mean(two_arr, axis=0))
    print("二维数组,对行求平均值:", np.mean(two_arr, axis=1))
    print("---------------- 使用dtype参数 ----------------")
    mean_dtype = np.mean(two_arr, dtype=np.float32)
    mean_no_dtype = np.mean(two_arr)
    print("二维数组,求平均值:{},类型:{} 不指定dtype时类型:{}".format(mean_dtype, type(mean_dtype), type(mean_no_dtype)))
    print("---------------- 使用keepdims ----------------")
    print("二维数组,求平均值;指定:keepdims:", np.mean(two_arr, keepdims=True))
    print("---------------- 使用where ----------------")
    print("一维数组,求平均值;指定:where > 20:", np.mean(one_arr, where=one_arr > 20))
    print("二维数组,求平均值;指定:where > 6:", np.mean(two_arr, where=two_arr > 6))

"""
---------------- 不指定参数时 ----------------
一维数组,求平均值: 25.0
二维数组,求平均值: 4.5
---------------- 使用axis参数 ----------------
二维数组,对列求平均值: [3. 4. 5. 6.]
二维数组,对行求平均值: [2.5 6.5]
---------------- 使用dtype参数 ----------------
二维数组,求平均值:4.5,类型:<class 'numpy.float32'> 不指定dtype时类型:<class 'numpy.float64'>
---------------- 使用keepdims ----------------
二维数组,求平均值;指定:keepdims: [[4.5]]
---------------- 使用where ----------------
一维数组,求平均值;指定:where > 20: 35.0
二维数组,求平均值;指定:where > 6: 7.5
"""    

2.3 中位数

np.median() 是用于计算数组的中位数的函数。

numpy.median(a, axis=None, out=None, overwrite_input=False, keepdims=False)

a.参数说明:

  • axis：指定计算中位数时要沿着哪个轴操作。默认值为 None，表示在整个数组上计算中位数。
  • out：可选参数，用于指定存储结果的输出数组。如果未提供，则创建一个新的数组来存储结果。
  • overwrite_input：可选参数，如果设置为 True，则允许直接修改输入数组以节省内存。默认值为 False。
  • keepdims：可选参数，如果设置为 True，则结果将保持与输入数组相同的维度。默认值为 False。

b. 代码示例:

import numpy as np

if __name__ == '__main__':
    # 一维数组
    one_arr = np.array([10, 20, 30, 40])
    print("一维数组中位数:", np.median(one_arr))
    # 二维数组
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("二维数组中位数:", np.median(two_arr))
    print("二维数组,沿行计算中位数:", np.median(two_arr, axis=1))
    print("二维数组，沿列计算中位数:", np.median(two_arr, axis=0))
    
"""
一维数组中位数: 25.0
二维数组中位数: 4.5
二维数组,沿行计算中位数: [2.5 6.5]
二维数组，沿列计算中位数: [3. 4. 5. 6.]
"""    

2.4 方差

方差是统计学中用来衡量一组数据的离散程度或分散程度的一种度量。它表示数据集中各个数据点与数据集均值之间的差异程度。方差越大，数据点相对于均值的分散程度就越高，方差越小，数据点相对于均值的分散程度就越低。

alt

a. 计算方差示例:

alt

在NumPy中使用函数np.var() 用于计算数组的方差。它的语法如下：

numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=False)

b. 参数说明:

  • axis：指定计算方差时要沿着哪个轴操作。默认值为 None，表示在整个数组上计算方差。
  • dtype：可选参数，用于指定结果的数据类型。默认值为 None，表示结果的数据类型由输入数组决定。
  • out：可选参数，用于指定存储结果的输出数组。如果未提供，则创建一个新的数组来存储结果。
  • ddof：可选参数，表示自由度的调整量。默认值为 0，表示标准的样本方差计算。通常在样本较小的情况下，将 ddof 设置为 1 以进行无偏估计。
  • keepdims：可选参数，如果设置为 True，则结果将保持与输入数组相同的维度。默认值为 False。

c.代码示例:

import numpy as np

if __name__ == '__main__':
    # 一维数组
    one_arr = np.array([5, 8, 12, 15, 20])
    print("一维数组方差:", np.var(one_arr))
    # 二维数组
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("二维数组方差:", np.var(two_arr))
    print("二维数组,沿行计算方差:", np.var(two_arr, axis=1))
    print("二维数组,沿列计算方差:", np.var(two_arr, axis=0))
    print("-------------------------- 指定:ddof ------------------------------")
    print("二维数组方差:", np.var(two_arr))
    print("二维数组,沿行计算方差:", np.var(two_arr, axis=1, ddof=1))
    print("二维数组,沿列计算方差:", np.var(two_arr, axis=0, ddof=1))
    
"""
一维数组方差: 27.6
二维数组方差: 5.25
二维数组,沿行计算方差: [1.25 1.25]
二维数组,沿列计算方差: [4. 4. 4. 4.]
-------------------------- 指定:ddof ------------------------------
二维数组方差: 5.25
二维数组,沿行计算方差: [1.66666667 1.66666667]
二维数组,沿列计算方差: [8. 8. 8. 8.]
"""    

2.5 标准差

标准差是一种用于度量数据集的离散程度或分散程度的统计指标，它是方差的平方根。标准差用于衡量数据点相对于数据集的均值的平均偏离程度，它提供了一种对数据集中数据分布的散布情况的直观认识。 标准差公式：

在NumPy中使用函数np.var() 用于计算数组的标准差，下面是代码示例:

import numpy as np

if __name__ == '__main__':
    # 一维数组
    one_arr = np.array([5, 8, 12, 15, 20])
    print("一维数组标准差:", np.std(one_arr))
    # 二维数组
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("二维数组标准差:", np.std(two_arr))
    print("二维数组,沿行计算标准差:", np.std(two_arr, axis=1))
    print("二维数组,沿列计算标准差:", np.std(two_arr, axis=0))
    
"""
一维数组标准差: 5.253570214625479
二维数组标准差: 2.29128784747792
二维数组,沿行计算标准差: [1.11803399 1.11803399]
二维数组,沿列计算标准差: [2. 2. 2. 2.]
"""    

2.6 最值

在numpy中,使用np.max()获取数组中最大值，使用np.min()获取数组中最小值；

import numpy as np

if __name__ == '__main__':
    # 一维数组
    one_arr = np.array([5, 8, 12, 15, 20])
    print("一维数组最大值:", np.max(one_arr))
    print("一维数组最小值:", np.min(one_arr))
    # 二维数组
    two_arr = np.array([
        [1, 2, 3, 4],
        [5, 6, 7, 8]
    ])
    print("二维数组最大值:", np.max(two_arr))
    print("二维数组最小值:", np.min(two_arr))
    print("------------------- 沿轴计算最值----------------------------")
    print("二维数组,沿行计算最大值:", np.max(two_arr, axis=1))
    print("二维数组,沿列计算最大值:", np.max(two_arr, axis=0))

"""
一维数组最大值: 20
一维数组最小值: 5
二维数组最大值: 8
二维数组最小值: 1
------------------- 沿轴计算最值----------------------------
二维数组,沿行计算最大值: [4 8]
二维数组,沿列计算最大值: [5 6 7 8]
"""    

3. 广播运算

3.1 介绍

NumPy中的广播（Broadcasting）是一种强大的特性，它允许在不同形状的数组之间执行元素级操作，而无需显式地将数组形状调整为相同的形状。这使得NumPy能够高效地执行各种元素级运算，而不需要额外的内存消耗。

具体广播的规则如下：

  • 规则1：如果两个数组的维度不同，将形状较小的数组的维度用1填充，直到两个数组的维度一致。
  • 规则2：如果两个数组在某个维度上相同或其中一个维度大小为 1，那么可以进行广播。
  • 规则3：如果两个数组在某个维度上的大小既不相同也不为1，则广播会失败，导致 ValueError

3.2 规则1-示例说明

规则1：如果两个数组的维度不同，将形状较小的数组的维度用1填充，直到两个数组的维度一致。

import numpy as np

if __name__ == '__main__':
    arr1 = np.array([1, 2, 3])  # 形状：(3,)
    print("数组1:", arr1)
    arr2 = np.array([[10], [20]])  # 形状：(2, 1)
    print("数组2:\n", arr2)
    result = arr1 + arr2
    print("广播规则1结果: \n", result)

"""
数组1: [1 2 3]
数组2:
 [[10]
 [20]]
广播规则1结果: 
 [[11 12 13]
 [21 22 23]]
"""    

说明: arr1 的形状是 (3,)，arr2 的形状是 (2, 1)，根据规则1，将 arr1 的形状用1填充，变为 (1, 3)，然后两个数组的维度一致，可以进行广播。

3.3 规则2-示例说明

规则2：如果两个数组在某个维度上相同或其中一个维度大小为 1，那么可以进行广播。

import numpy as np

if __name__ == '__main__':
    arr1 = np.array([[1, 2, 3], [4, 5, 6]])  # 形状：(2, 3)
    print("arr1:\n", arr1)
    arr2 = np.array([10, 20, 30])  # 形状：(3,)
    print("arr2:", arr2)
    result = arr1 + arr2
    print("广播规则2结果: \n", result)

"""
arr1:
 [[1 2 3]
 [4 5 6]]
arr2: [10 20 30]
广播规则2结果: 
 [[11 22 33]
 [14 25 36]]
"""    

说明: 在进行广播时，NumPy会从最右边的维度开始比较。在这种情况下，arr2 的最右边的维度大小为 3，而 arr1 的对应维度大小也为 3。满足规则2，可以进行广播。

3.4 规则3-示例说明

如果两个数组在某个维度上的大小既不相同也不为1，则广播会失败，导致 ValueError。

import numpy as np

if __name__ == '__main__':
    arr1 = np.array([[1, 2, 3], [4, 5, 6]])  # 形状：(2, 3)
    print("arr1:\n ", arr1)
    arr2 = np.array([10, 20])  # 形状：(2,)
    print("arr2:", arr2)
    try:
        result = arr1 + arr2
    except ValueError as e:
        result = "ValueError: {}".format(e)

    print("广播规则3结果:", result)
    
"""
arr1:
  [[1 2 3]
 [4 5 6]]
arr2: [10 20]
广播规则3结果: ValueError: operands could not be broadcast together with shapes (2,3) (2,) 
"""    

说明: 在进行广播时，NumPy会从最右边的维度开始比较。在这种情况下，arr2 的最右边的维度的大小为2，而 arr1 的对应维度的大小为3。这两个大小既不相同，也不为1，因此广播规则3被触发，导致广播失败。

4. 矩阵运算

4.1 创建矩阵

在NumPy中,矩阵本质上也是一个数组，拥有数组的所有属性和方法；但矩阵又有一些不同于数组的特性和方法。如下:

  • 矩阵是二维的，不能像数组一样幻化成任意维度。
  • 矩阵的乘法不同于数组乘法。

在NumPy中，可以使用np.mat()和np.matrix()创建矩阵，如下代码示例:

import numpy as np

if __name__ == '__main__':
    # 使用np.matrix创建矩阵
    matrix_a = np.matrix([[1, 2], [3, 4]])
    print("matrix_a: \n {} \n matrix_a类型:{}".format(matrix_a, type(matrix_a)))
    # 使用mat创建矩阵
    matrix_b = np.mat(np.arange(4).reshape(2, 2))
    print("matrix_b: \n {} \n matrix_b类型:{}".format(matrix_b, type(matrix_b)))
    
"""
matrix_a: 
 [[1 2]
 [3 4]] 
 matrix_a类型:<class 'numpy.matrix'>
matrix_b: 
 [[0 1]
 [2 3]] 
 matrix_b类型:<class 'numpy.matrix'>
"""    

4.2 矩阵特有属性

矩阵有几个特有的属性，如转置矩阵、逆矩阵、共轭矩阵、共轭转置矩阵等

import numpy as np

if __name__ == '__main__':
    # 使用mat创建矩阵
    matrix_a = np.mat(np.arange(6).reshape(2, 3))
    print("matrix_a: \n", matrix_a)
    # 获取其转置矩阵
    print("matrix_a转置矩阵: \n", matrix_a.T)
    # 获取其共轭转置矩阵
    print("matrix_a共轭转置矩阵: \n", matrix_a.H)
    # 获取其逆矩阵
    print("matrix_a逆矩阵: \n", matrix_a.I)
    # 获取其数据的视图（ndarray类）
    print("matrix_a其数据的视图: \n", matrix_a.A)
    print("matrix_a其数据的视图-类型: \n", type(matrix_a.A))
    
"""
matrix_a: 
 [[0 1 2]
 [3 4 5]]
matrix_a转置矩阵: 
 [[0 3]
 [1 4]
 [2 5]]
matrix_a共轭转置矩阵: 
 [[0 3]
 [1 4]
 [2 5]]
matrix_a逆矩阵: 
 [[-0.77777778  0.27777778]
 [-0.11111111  0.11111111]
 [ 0.55555556 -0.05555556]]
matrix_a其数据的视图: 
 [[0 1 2]
 [3 4 5]]
matrix_a其数据的视图-类型: 
 <class 'numpy.ndarray'>
"""    

4.3 矩阵乘法

并不是所有的矩阵都可以直接相乘，需要满足一定规则，才可以进行矩阵乘法运算，规则如下:

  • 列数等于行数： 第一个矩阵的列数必须等于第二个矩阵的行数。如果第一个矩阵的形状是 (m, n)，那么第二个矩阵的形状应该是 (n, p)。两个矩阵相乘的结果将是一个新矩阵，其形状为 (m, p)。
  • 对应维度的大小要一致： 除了满足列数等于行数的条件外，对应维度的大小也需要一致。具体来说，第一个矩阵的列数要与第二个矩阵的行数一致。如: 矩阵 A 形状为 (3, 2) 和矩阵 B 形状为 (2, 4)，对应维度的大小是2，它们是一致的。 
import numpy as np

if __name__ == '__main__':
    # 使用mat创建矩阵
    matrix_a = np.mat(np.random.randint(1, 10, size=(4, 2)))
    print("matrix_a: \n", matrix_a)
    matrix_b = np.mat(np.random.randint(1, 10, size=(2, 3)))
    print("matrix_b: \n", matrix_b)
    print("matrix_dot: \n", matrix_a.dot(matrix_b))
    print("matrix_dot2: \n", matrix_a * matrix_b)
    
"""
matrix_a: 
 [[4 1]
 [8 2]
 [7 8]
 [3 4]]
matrix_b: 
 [[7 7 3]
 [3 5 7]]
matrix_dot: 
 [[31 33 19]
 [62 66 38]
 [73 89 77]
 [33 41 37]]
matrix_dot2: 
 [[31 33 19]
 [62 66 38]
 [73 89 77]
 [33 41 37]]
"""    

对于数组而言，使用*相乘和使用np.dot函数相乘是完全不同的两种乘法；对于矩阵来说，不管是使用*相乘还是使用np.dot函数相乘，结果都是np.dot函数相乘的结果，因为矩阵没有对应元素相乘这个概念。

下图是两个矩阵相乘时,如果计算出结果的示意图

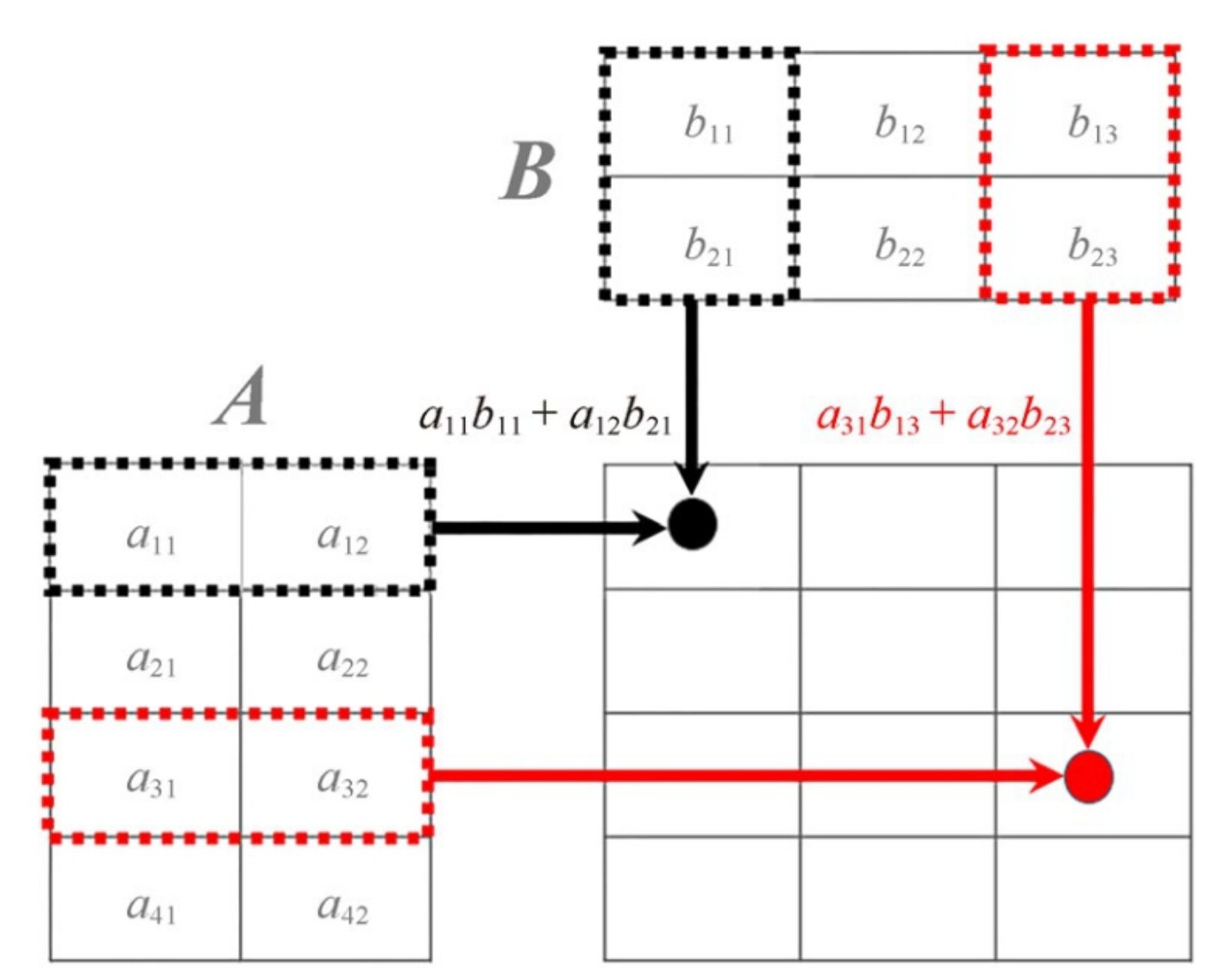
图片来自: 《Python高手修炼之道: 数据处理与机器学习实战》
图片来自: 《Python高手修炼之道: 数据处理与机器学习实战》

本文由 mdnice 多平台发布

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/154518.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

IntelliJ IDEA失焦自动重启服务的解决方法

IntelliJ IDEA失焦自动重启服务的解决方法

IDEA 热部署特性 热部署&#xff0c;即应用正属于运行状态时&#xff0c;我们对应用源码进行了修改更新&#xff0c;在不重新启动应用的情况下&#xff0c;可以能够自动的把更新的内容重新进行编译并部署到服务器上&#xff0c;使修改立即生效。 现象 在使用 IntelliJ IDEA运…
阅读更多...
实现基于 GitLab 的数据库 CI/CD 最佳实践

实现基于 GitLab 的数据库 CI/CD 最佳实践

数据库变更一直是整个应用发布过程中效率最低、流程最复杂、风险最高的环节&#xff0c;也是 DevOps 流程中最难以攻克的阵地。那我们是否能在具体的 CI/CD 流程中&#xff0c;像处理代码那样处理数据库变更呢&#xff1f; DORA 调研报告 DORA&#xff08;DevOps Research &am…
阅读更多...
练[GYCTF2020]EasyThinking

练[GYCTF2020]EasyThinking

[GYCTF2020]EasyThinking 文章目录 [GYCTF2020]EasyThinking掌握知识解题思路还得靠大佬正式开始 关键paylaod 掌握知识 ​ thinkphpV6任意文件操作漏洞&#xff0c;代码分析写入session文件的参数&#xff0c;源码泄露&#xff0c;使用蚁剑插件disable_functions绕过终端无回…
阅读更多...
【算法设计与分析】— —单源最短路径的贪心算法

【算法设计与分析】— —单源最短路径的贪心算法

&#x1f383;欢迎大家前去观看我的算法设计与分析专栏&#xff1a; 算法设计与分析_IT闫的博客-CSDN博客 希望对大家有所帮助&#xff01; &#x1f383;个人专栏&#xff1a; &#x1f42c; 算法设计与分析&#xff1a;算法设计与分析_IT闫的博客-CSDN博客 &#x1f433;Java…
阅读更多...
Spring 复习笔记

Spring 复习笔记

目录 第一步存 Bean第二步获取并使用 Bean依赖查找的方式ApplicationContext vs BeanFactory 更简单的存储 Bean1. 配合五大类注解使用2. 方法上添加注解 Bean 更简单的获取 Bean Spring IoC 容器管理的资源就是对象&#xff0c;这个对象也叫做 Bean。Spring 作为一个 IoC 容器…
阅读更多...
zabbix自定义监控内容和自动发现

zabbix自定义监控内容和自动发现

6 目录 一、自定义监控内容&#xff1a; 1.明确需要执行的 linux 命令 2.创建 zabbix 的监控项配置文件&#xff0c;用于自定义 key&#xff1a; 3. 在 Web 页面创建自定义监控项模板&#xff1a; 3.1 创建模板&#xff1a; 3.2 创建监控项&#xff1a; 3.3 创建触发器&#…
阅读更多...
VxeTable 表格组件推荐

VxeTable 表格组件推荐

VxeTable 表格组件推荐 https://vxetable.cn 在前端开发中&#xff0c;表格组件是不可或缺的一部分&#xff0c;它们用于展示和管理数据&#xff0c;为用户提供了重要的数据交互功能。VxeTable 是一个优秀的 Vue 表格组件&#xff0c;它提供了丰富的功能和灵活的配置选项&…
阅读更多...
关于优先队列的一点细节

关于优先队列的一点细节

在使用优先队列PriorityQueue时&#xff0c;默认的是升序排列&#xff0c;自己可以指定比较器改为降序排列&#xff0c;例如Collections.reverseOrder()等。 但是在我做力扣的过程中&#xff0c;简单的用一个list的addAll方法添加了优先队列里边所有元素&#xff0c;结果发现添…
阅读更多...
【Spring】Spring MVC 程序开发

【Spring】Spring MVC 程序开发

Spring MVC 程序开发 一. 什么是 Spring MVC1. MVC2. Spring、Spring Boot 与 Spring MVC 二. 创建 Spring MVC 项目1. 创建项目2. 用户和程序的映射3. 获取用户请求参数①. 获取单个参数②. 获取多个参数③. 传递对象④. 后端参数重命名&#xff08;后端参数映射&#xff09;R…
阅读更多...
Django开发之进阶篇

Django开发之进阶篇

Django进阶篇 一、Django学习之模板二、Django学习之中间件默认中间件自定义中间件 三、Django学习之ORM定义模型类生成数据库表操作数据库添加查询修改删除 一、Django学习之模板 在 Django 中&#xff0c;模板&#xff08;Template&#xff09;是用于生成动态 HTML&#xff…
阅读更多...
vue-6

vue-6

一、声明式导航-导航链接 1.需求 实现导航高亮效果 如果使用a标签进行跳转的话&#xff0c;需要给当前跳转的导航加样式&#xff0c;同时要移除上一个a标签的样式&#xff0c;太麻烦&#xff01;&#xff01;&#xff01; 2.解决方案 vue-router 提供了一个全局组件 router…
阅读更多...
【PickerView案例13-应用程序对象介绍 Objective-C语言】

【PickerView案例13-应用程序对象介绍 Objective-C语言】

一、应用程序对象介绍： 1.应用程序对象介绍： 应用程序介绍： 应用程序介绍： 应用程序介绍： 应用程序启动，本身这一过程，不是应用程序启动就完事儿了， 它有一些比较细节的东西，比如说： 1）info.plist以及pch文件 2）UIApplication对象 这个呢，我们都是分开的去说，…
阅读更多...
北斗高精度定位为无人车成为机场运营新常态提供技术保障

北斗高精度定位为无人车成为机场运营新常态提供技术保障

在现代快节奏的生活中&#xff0c;人们对交通效率和安全性的需求越来越高。为了满足这一需求&#xff0c;无人驾驶技术被广泛研究和应用。而随着北斗卫星系统的发展&#xff0c;机场无人车正成为潜在的未来运输解决方案。本文将深入探讨北斗卫星如何改变机场运营&#xff0c;以…
阅读更多...
一站式数据可视化与分析平台JVS智能BI强大的数据节点功能

一站式数据可视化与分析平台JVS智能BI强大的数据节点功能

在商业智能&#xff08;BI&#xff09;中&#xff0c;数据集是数据的集合&#xff0c;用于分析和报告。数据节点是数据集中的一个重要组成部分&#xff0c;它代表数据集中的一个特定数据点或数据元素。通过使用数据节点&#xff0c;可以对数据进行过滤、分组和计算&#xff0c;…
阅读更多...
2785323-77-3，MAL-Alkyne，双功能连接试剂Alkyne maleimide

2785323-77-3，MAL-Alkyne，双功能连接试剂Alkyne maleimide

炔烃马来酰亚胺&#xff0c;Alkyne maleimide,MAL-Alkyne是一种非常有用的双功能连接试剂&#xff0c;可以在生物分子中发挥重要的作用。它的马来酰亚胺基团可以与生物分子中的硫醇基团反应&#xff0c;形成共价键&#xff0c;从而将生物分子与炔烃连接起来。这种连接方式在生物…
阅读更多...
将 Ordinals 与比特币智能合约集成：第 3 部分

将 Ordinals 与比特币智能合约集成：第 3 部分

基于 Ordinals 的 BSV-20 同质化代币 之前&#xff0c;我们展示了如何将比特币智能合约与 Ordinals 集成&#xff0c;Ordinals 可以被视为链上的 NFT。 在本文中&#xff0c;我们将展示如何将它们与同质化代币&#xff08;即 BSV-20 代币&#xff09;集成。 我们仍然以拍卖为例…
阅读更多...
【数据库——MySQL（实战项目1）】（2）图书借阅系统

【数据库——MySQL（实战项目1）】（2）图书借阅系统

目录 1. 简述2. 功能代码2.1 创建视图显示所有逾期未归还的借阅信息&#xff08;包括借阅人姓名&#xff0c;借阅人类别&#xff0c;书名&#xff0c;借出日期&#xff0c;应归还日期&#xff0c;逾期时长&#xff09;&#xff1b;2.2 创建存储过程&#xff0c;每借出一本图书&…
阅读更多...
【算法笔记】LCR 086. 分割回文串

【算法笔记】LCR 086. 分割回文串

基本思想是使用回溯法&#xff0c;回溯法都可以将问题划分为一个解空间树&#xff1a;假设字符串s为"aab"&#xff0c;那么我们可以使用深度优先搜索去构建解空间树&#xff1a; dfs遍历出来的第一个序列是[a, a, b]&#xff0c;显然该序列都是回文子串&#xff0c;…
阅读更多...
前后端分离项目-基于springboot+vue的足球青训俱乐部管理后台系统的设计与实现（内含代码+文档+报告）

前后端分离项目-基于springboot+vue的足球青训俱乐部管理后台系统的设计与实现（内含代码+文档+报告）

博主介绍&#xff1a;✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久&#xff0c;选择我们就是选择放心、选择安心毕业✌ &#x1f345;由于篇幅限制&#xff0c;想要获取完整文章或者源码&#xff0c;或者代做&am…
阅读更多...
colab切换目录的解决方案

colab切换目录的解决方案

大家好，我是爱编程的喵喵。双985硕士毕业，现担任全栈工程师一职，热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023