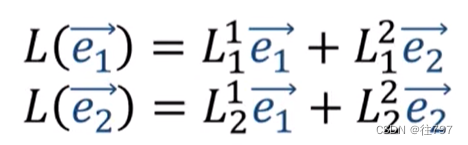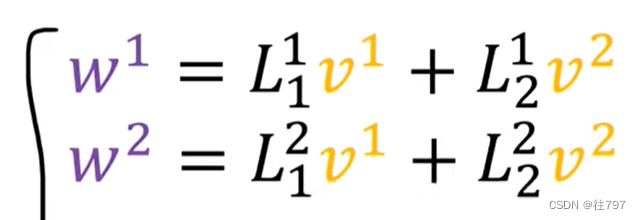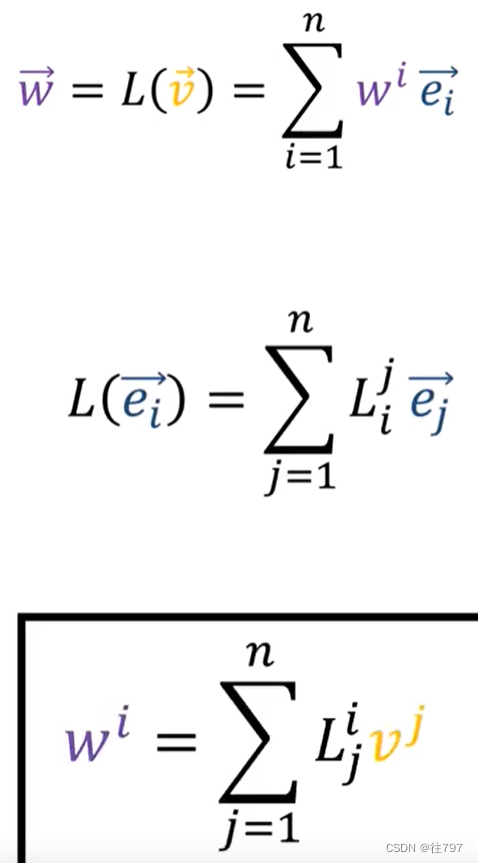线性映射
线性映射是将向量作为输入并产生一些新向量作为输出的转换。
从坐标定义开始(数组),再到2,3,并展示它们是如何关联的
线性映射的坐标表示最终是矩阵,
1.坐标定义(数组)
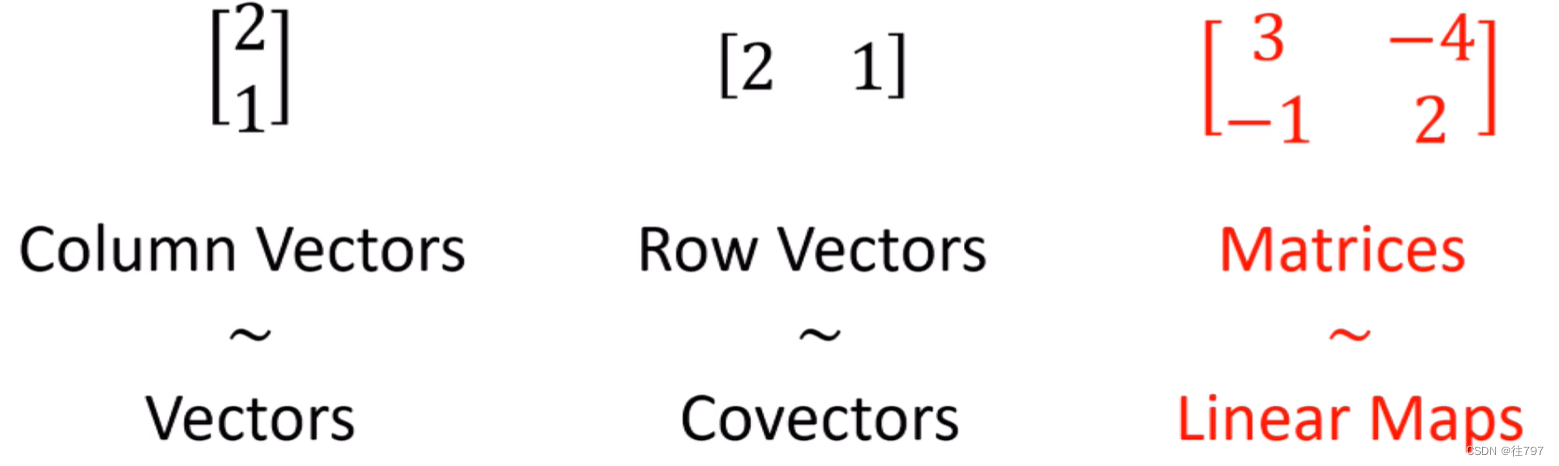
列向量是向量的坐标表示。
行向量是协向量的坐标表示。
矩阵是线性映射的坐标表示。
矩阵是如何转变向量的?
例子
现有一个作用于2x1列向量的2x2矩阵,输出的向量是?
但仅通过查看矩阵中的数字来理解矩阵在做什么会让人感到困惑。
但对所有这些数字的含义,有一个简单的解释:
注意,若使用列向量 作为输入,将得到矩阵的第一列作为输出。
若使用列向量 作为输入, 将得到矩阵的第二列作为输出。
现这些列向量 、
, 它们有点像基向量e1、e2的副本,
之所以说是像副本,是因为这里非常重要的一点:线性映射转换向量,但是线性映射不转换基向量!
因此,当使用线性映射转换向量时,基底是不会变的。 我们不会移动基底,


虽然输出向量可能与输入向量不同,但我们仍将使用相同的基底来测量输出向量,但话虽如此,对于矩阵,第 i 列会告诉你将第 i 个基向量的副本映射到哪里。
因此,从视觉上观察一下,
现有两基底:e1、e2,还有两向量v,w。v和w有点像e1、e2的副本,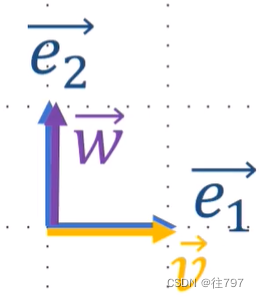
有个矩阵如下:
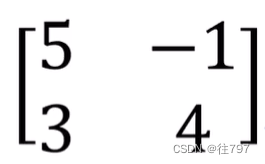
那么该矩阵会将向量v(v像e1的副本)发送到哪?
只看矩阵的第一列,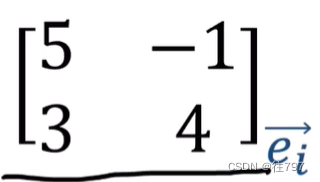
它表示向量5e1+3e2 , 这就是线性映射的输出,![]()
V在视觉上:
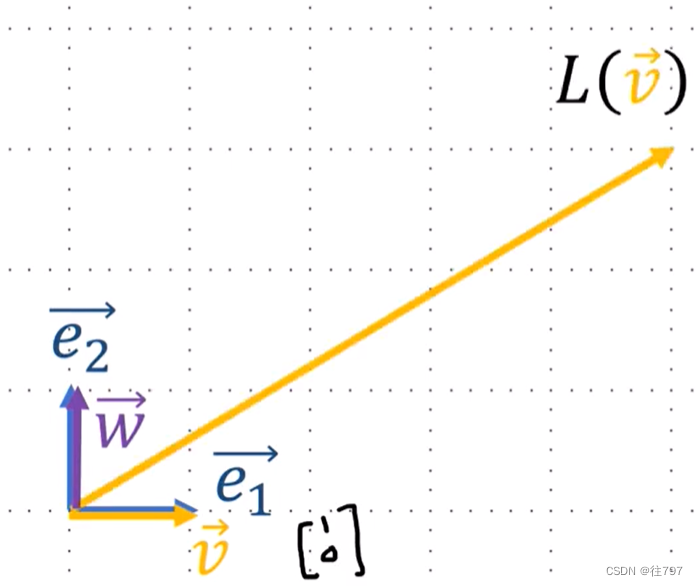
矩阵对向量w(e2的副本)做了什么?
看矩阵的第二列,给我们输出 -e1+4e2
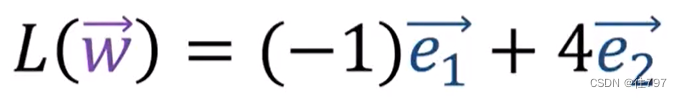
视觉上:
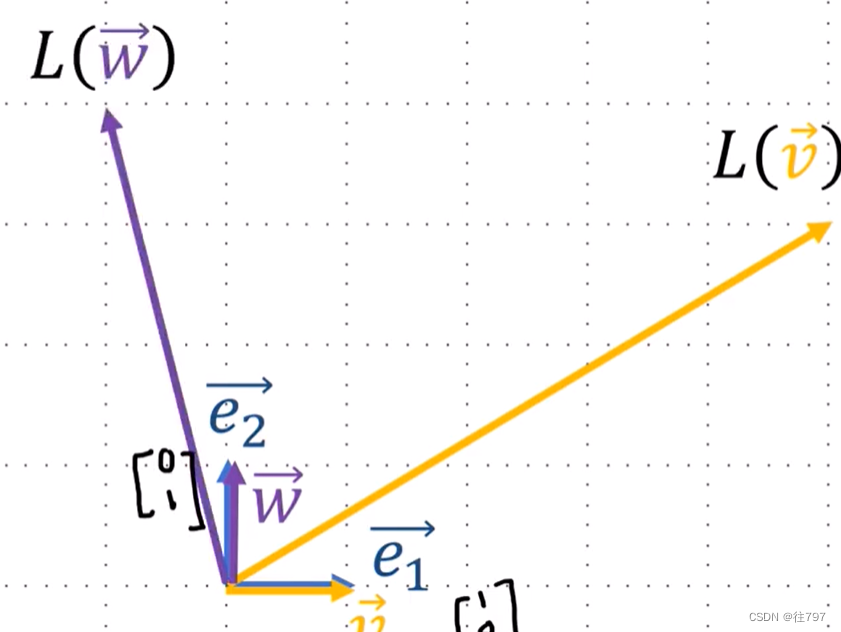
注意到,基向量没有移动,因为线性映射不会改变基底,我们仍用相同的基底测量输出向量,
所以,综上,矩阵是线性映射的坐标解释。
2.几何定义(线性映射视为图片)
线性映射 是 空间转换,并且保持线平行, 保持线间隔均匀,保持原点静止。
为从视觉上了解它的外观,从2D空间开始,上面有一堆网格线:
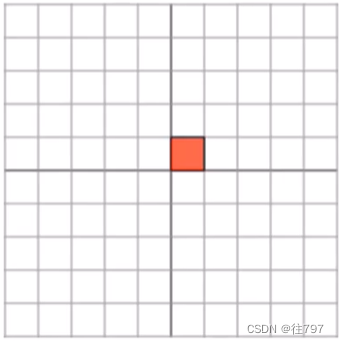 (初始的输入空间?)
(初始的输入空间?)
这里有三个线性映射的例子:
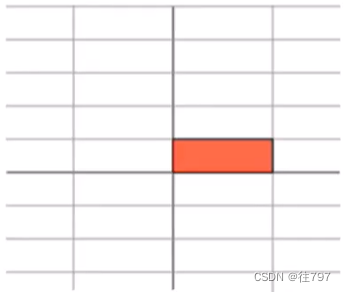
所以,上面这个线性映射基本上只是水平方向的拉伸。
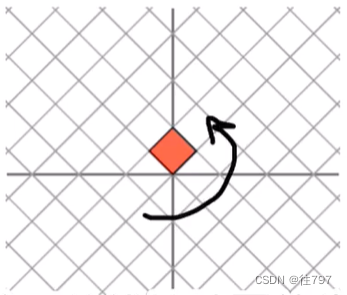 这个线性映射像一个旋转,
这个线性映射像一个旋转,
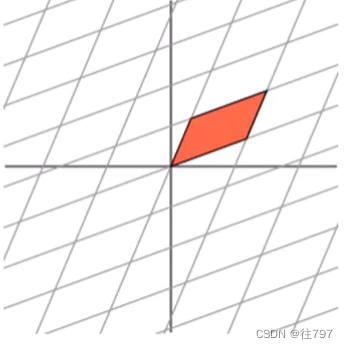
这个线性映射像做一个倾斜变换(可把它想象成在这个方向上做一个旋转,然后沿着这个轴伸展)。
正如上面这些图所示,在所有这些情况下, 输出空间中的网格线仍然彼此平行, 都是均匀分布的(即使间距与输入空间不同),并且原点没有移动。
所有的上面这些都是线性映射可以做到的。
(注意,在该定义下,translation are not linear maps------平移不是线性映射。即使平移能使得网格线平行,间距均匀,但平移会移动原点,所以平移不是线性映射)
所以,这就是可视化的几何定义。
3.抽象定义(纯代数)
线性映射 是将 向量 映射 到 向量 的函数。
在该情况下,现有一映射L将 向量从向量空间V 映射到 向量空间W,我们很多例子涉及到的映射是从空间V映射到 空间V, 但一般来说,输入和输出空间可以不同。
且线性映射在这里遵循两个属性:
1、可添加线性映射的输入或输出并得到相同的答案。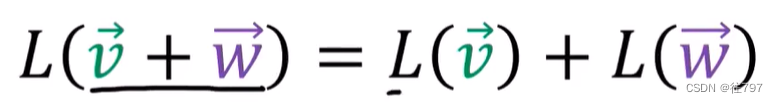
2.可缩放输入或缩放输出并得到相同的答案。
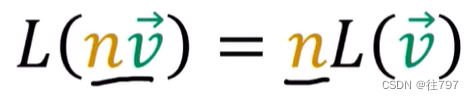
这两个属性被称为“线性”、 。 所以协向量和线性映射都是线性函数。唯一的区别是:协向量输出一个标量,线性映射输出向量。
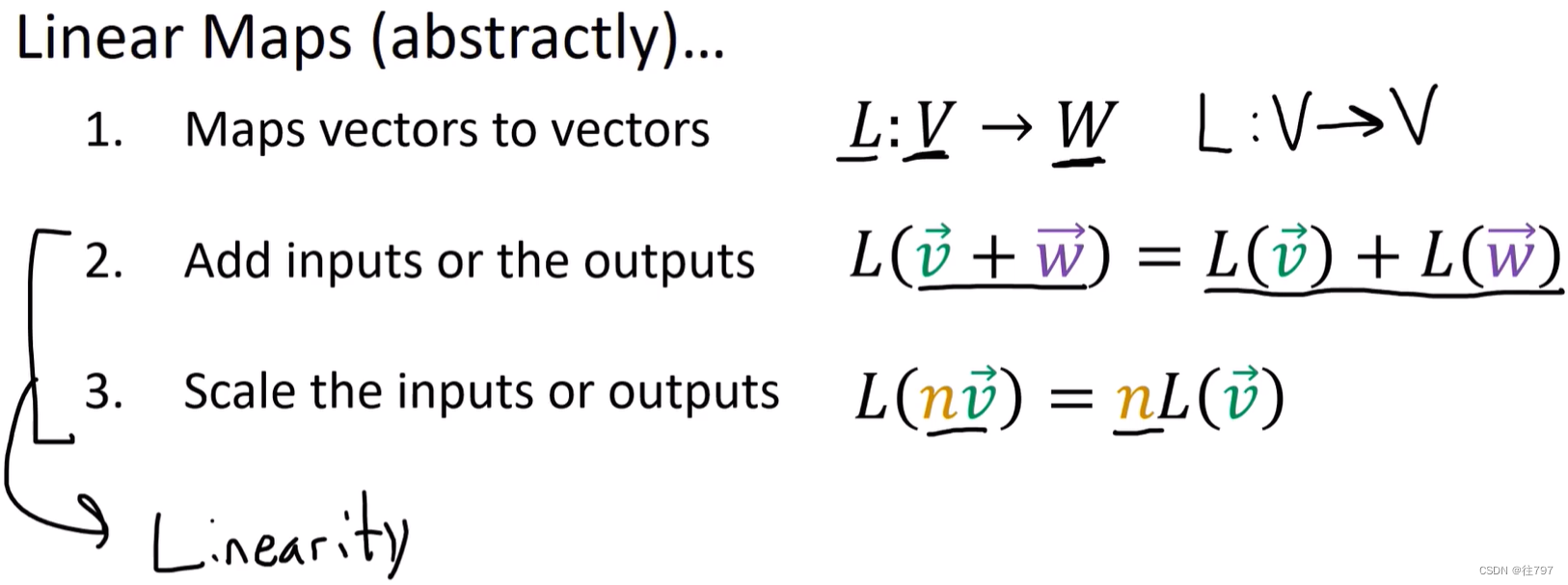
下面展示 这个抽象定义 如何 与我们看到的其他定义相关联。
如前所说,有这个属性:
![]()
现展示它的几何意义,在网格上绘制输入变量,这里我们有绿色的向量v和紫色的向量w,
v+w 用黑色表示。
现展示这图中的三个线性映射是如何服从这个代数性质的。

在这些所有的输出空间中可以看到,加法定律仍然有效,
对缩放规则(第二个属性)也做同样的事情。
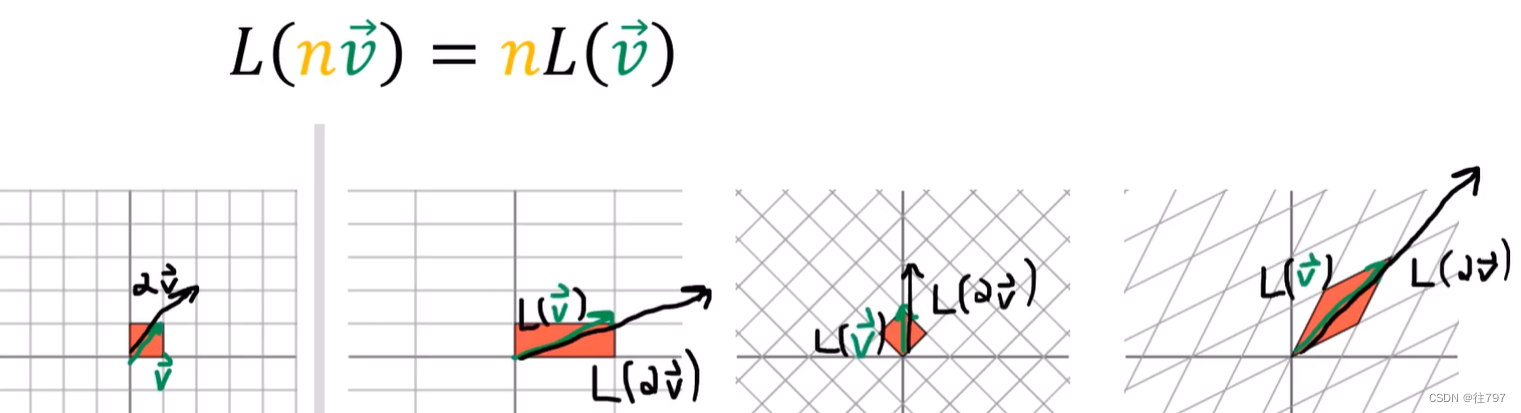
因此,先缩放再转换 与 先转换再缩放 是一回事。
还有一个问题,坐标定义的来源
对于下图这个矩阵乘法公式,若你不知道它背后的原因,它看起来真的很奇怪。
事实证明,矩阵乘法规则实际上来自上面这个抽象定义,
证明:
首先我们有一个线性映射L,它作用于向量V,并产生输出向量W,
若将向量V拓展成它的分量,就能得到
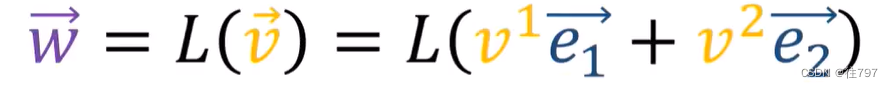
通过L的线性规则,得到: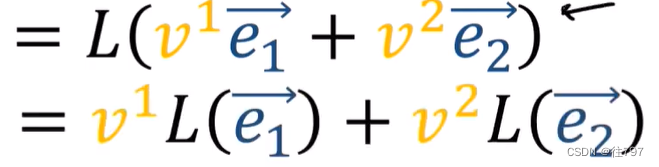
e1、e2是向量,所以你可能会问如何根据 基底e1、e2来表达这些向量,
现做个 简单的假设:
假设线性映射L是从V到V的函数,因此输入空间和输出空间是相同的。
因此,输出空间V仍然具有基底e1、e2,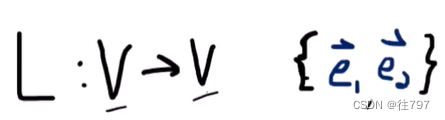
这意味着我们仍然可以将 这些输出向量 写为相同的旧基 e1、e2的线性组合,
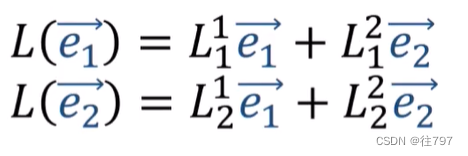
而这些线性组合的系数,
这些L系数帮助我们使用“e”基底向量构建线性映射的输出向量。
所以,可以将输出向量重写为基的线性组合,并且可在此切换内容为以按基向量e1、e2来重新分组,
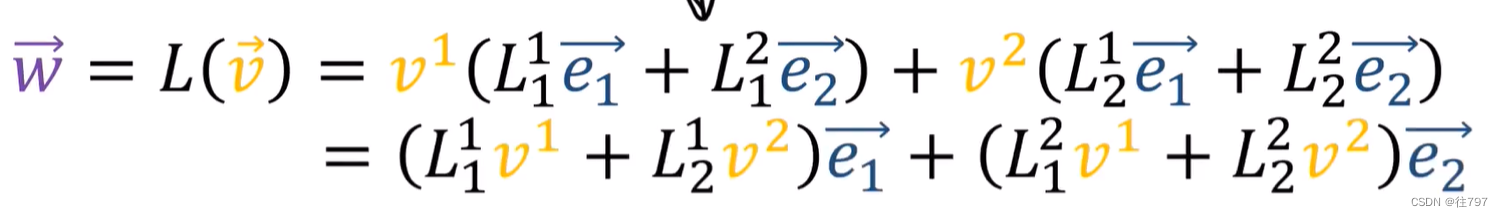
现在,由于将W写成基向量的线性组合,
因此,这些系数 实际上 只是W的分量:w1、w2 ,
所以现在我们已经推到出 如何使用这些公式将V系数转换为W系数,
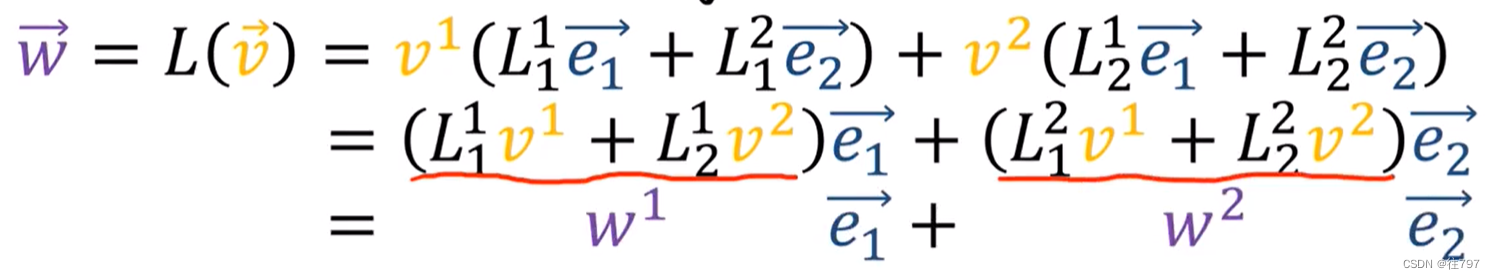
而这些公式 就是那些当你做标准的2x2矩阵乘以一个2x1的列向量。
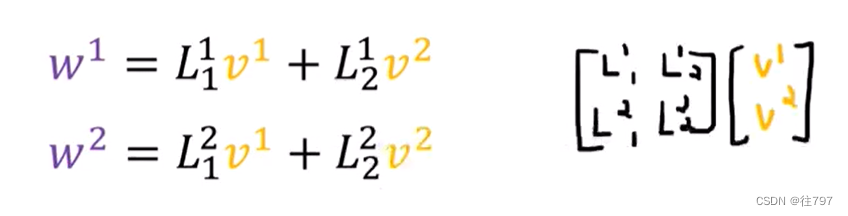
现总结一下,如果我们有一个线性映射L,它可以像这样将向量V转换为另一个向量W,其中W可以写成基底的线性组合,并且我门知道如何使用L系数转换基底(或者说我们知道L如何转换基向量副本可能更好)
这意味着我们可以在这里使用这些公式将V分量变为W分量。
如果对任意数量的维度重复这个论点,如果我们有一个n维的线性映射L,
我们将从这里的公式中得到所有的L系数,然后可以使用这个公式将V分量转换为W分量,