深入探索BP神经网络【简单原理、实际应用和Python示例】

人工神经网络（Artificial Neural Networks）是一种受到生物神经网络启发的机器学习模型，它的应用范围广泛，包括图像识别、语音识别、自然语言处理等领域。其中，BP神经网络（Backpropagation Neural Network）是最常见和基础的神经网络之一。

背景

BP神经网络是一种 前馈神经网络，最早由David Rumelhart、Geoffrey Hinton和Ron Williams于1986年提出。它的设计灵感来自于 人脑中神经元之间的信息传递机制，通过神经元之间的连接和权重来模拟信息处理 。BP神经网络由输入层、隐含层（可以有多个）、输出层组成，每个神经元都与上一层的所有神经元相连，每个连接都有一个权重。

它就像一条信息流水管，把信息从一头输送到另一头。想象一下，你把一些问题的答案输入到这个水管的一端，然后它通过一系列的阀门和管道，最终给你正确的答案。这些阀门和管道就是我们的神经元，而它们之间的强弱连接就是权重。

与前馈神经网络不同，后馈神经网络 在信息传递方面更加复杂。前馈神经网络只向前传递信息，而后馈神经网络可以在信息传递的同时，也允许信息反馈，形成循环。这使得后馈神经网络在处理某些复杂问题时更加强大，但也更加复杂。虽然后馈神经网络在某些情况下非常有用。

解决的问题

BP神经网络主要用于解决分类和回归问题。它可以应用于诸如图像分类、文本情感分析、手写数字识别等任务。通过学习和调整神经元之间的权重，BP神经网络可以自动地发现输入数据中的模式和特征，从而进行准确的预测和分类。

实现原理

梯度下降算法

BP神经网络的训练基于梯度下降算法。该算法的核心思想是最小化损失函数，使预测值与实际值之间的误差尽可能小。下面是梯度下降算法的关键步骤：

初始化权重和偏置： 刚开始，我们给网络的每个"连接"（类似神经元之间的道路）随机设置了一些权重，就像是在城市的交叉口上设置了一些标志。
前向传播： 我们把数据传递给网络，就像是车辆在城市中行驶，经过每个交叉口。每个神经元计算出一些东西，就像是每个交叉口告诉车辆往哪里走。
计算损失： 我们想要知道网络的预测是否准确，所以我们计算出它的错误，就像是检查车辆是否按照地图行驶。
反向传播： 然后，我们回头看每个连接的错误，就像是回头看每个交叉口上的标志是否设置得合适。如果错了，我们会微调标志，就像是微调道路的方向。
重复迭代： 我们一遍又一遍地重复这个过程，每次都试图让预测更准确。就像是一辆车一步一步地走向正确的目的地，最终我们希望网络的预测变得非常准确，损失变得很小。

代码示例

以下将演示如何使用BP神经网络解决二分类问题（解决XOR问题）

import numpy as np
import matplotlib.pyplot as plt# 定义激活函数
def sigmoid(x):return 1 / (1 + np.exp(-x))# 初始化权重和偏置
input_size = 2
hidden_size = 3
output_size = 1
learning_rate = 0.1w1 = np.random.randn(input_size, hidden_size)
b1 = np.zeros((1, hidden_size))
w2 = np.random.randn(hidden_size, output_size)
b2 = np.zeros((1, output_size))# 训练数据
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])# 存储损失值
losses = []# 训练神经网络
for epoch in range(10000):# 前向传播z1 = np.dot(X, w1) + b1a1 = sigmoid(z1)z2 = np.dot(a1, w2) + b2a2 = sigmoid(z2)# 计算损失loss = np.mean((a2 - y) ** 2)losses.append(loss)# 反向传播dloss_da2 = 2 * (a2 - y)da2_dz2 = a2 * (1 - a2)dz2_dw2 = a1dz2_db2 = 1dloss_dw2 = np.dot(dz2_dw2.T, dloss_da2 * da2_dz2)dloss_db2 = np.sum(dloss_da2 * da2_dz2, axis=0, keepdims=True)da2_dz1 = w2dz1_dw1 = Xdz1_db1 = 1dloss_da1 = np.dot(dloss_da2 * da2_dz2, da2_dz1.T)dloss_dw1 = np.dot(dz1_dw1.T, dloss_da1 * sigmoid(z1) * (1 - sigmoid(z1)))dloss_db1 = np.sum(dloss_da1 * sigmoid(z1) * (1 - sigmoid(z1)), axis=0, keepdims=True)# 更新权重和偏置w1 -= learning_rate * dloss_dw1b1 -= learning_rate * dloss_db1w2 -= learning_rate * dloss_dw2b2 -= learning_rate * dloss_db2if epoch % 1000 == 0:print(f'Epoch {epoch}, Loss: {loss}')# 使用训练好的模型进行预测
def predict(X):z1 = np.dot(X, w1) + b1a1 = sigmoid(z1)z2 = np.dot(a1, w2) + b2a2 = sigmoid(z2)return a2# 测试
X_test = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
predictions = predict(X_test)
print("Predictions:")
print(predictions)# 绘制损失曲线
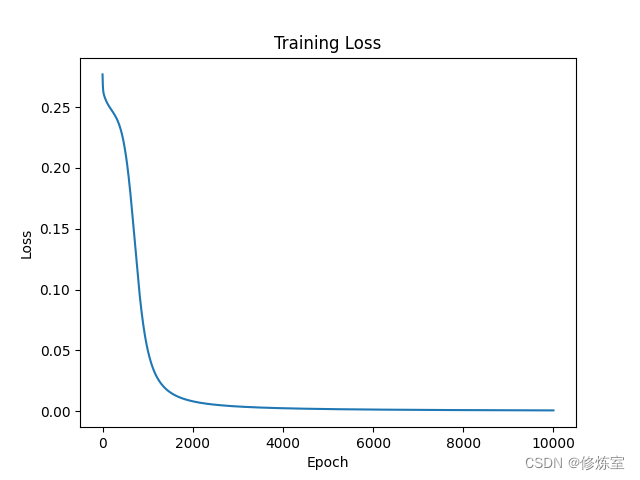
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss')
plt.show()

在上述代码中，各个变量的意义如下：

w1：第一层权重矩阵，它包含了输入数据到隐含层神经元的连接权重。其形状为 (input_size, hidden_size)，其中 input_size 是输入特征的数量，hidden_size 是隐含层神经元的数量。
b1：第一层偏置，它包含了隐含层每个神经元的偏置。其形状为 (1, hidden_size)，用于调整神经元的激活阈值——如果偏置值很大，神经元更容易被激活；如果偏置值很小，神经元更难被激活
w2：第二层权重矩阵，它包含了隐含层到输出层神经元的连接权重。其形状为 (hidden_size, output_size)，其中 output_size 是输出层神经元的数量。
b2：第二层偏置，它包含了输出层每个神经元的偏置。其形状为 (1, output_size)，用于调整输出层神经元的激活阈值。
X：训练数据集，包含输入数据的矩阵。其形状为 (样本数, input_size)，其中 样本数 表示训练数据的数量。
y：目标输出数据，包含每个样本的目标输出。其形状为 (样本数, output_size)。
losses：用于存储每个训练周期（epoch）中的损失值。损失是模型的预测与实际目标的误差。
input_size：输入特征的数量，通常等于 X 矩阵的列数。
hidden_size：隐含层神经元的数量，是神经网络结构中的一个超参数。
output_size：输出层神经元的数量，通常等于 y 矩阵的列数。
learning_rate：学习率，用于控制权重和偏置的更新步长。这是一个超参数，影响训练过程的速度和稳定性。

如何理解超参数？
“超” 表示它们在神经网络模型中处于更高的层次，是一种 控制参数的参数，是我们手动设置的。它们影响着训练的方式和结果，但不是从数据中学习得到的，两个常见的超参数是：

隐含层神经元数量（hidden_size）： 这就好像是一个神秘的房间，我们在这个房间里进行了一些数学运算，以便理解和解决问题。但我们需要决定房间里有多少人。如果人太多，可能会变得复杂而慢，如果人太少，可能无法解决复杂的问题。所以，hidden_size 是一个数字，帮助我们控制神经网络中这个房间里有多少“工作人员”。
学习率（learning_rate）： 学习率就像是我们在学校学习的速度。如果我们学习得太快，可能会错过重要的东西；如果我们学习得太慢，可能会浪费时间。所以，learning_rate 是一个数字，它帮助我们控制在训练神经网络时，我们每次更新权重和偏置的速度。如果它太大，可能导致不稳定，如果太小，训练可能会很慢。

这两个超参数，hidden_size 和 learning_rate，是我们在构建神经网络时需要做的决策，它们会影响我们的模型是如何工作的。所以，选择适合问题的隐含层神经元数量和学习率非常重要。学习率要选择得当，使得模型在训练过程中能够迅速学习，同时又保持稳定，而隐含层神经元数量要足够适应问题的复杂度，但也不能过多，以免增加计算负担。

在上述代码中，用到的三个函数的简单解释：

np.random.randn：这是一个用于生成随机数的函数。它创建一个包含随机数的数组，这些随机数遵循标准 正态分布 （均值为0，标准差为1）。在神经网络中，我们通常使用这些随机数来初始化神经网络的权重，使它们具有随机的初始值。
np.zeros：这个函数用于创建一个数组，其中所有的元素都是零。在神经网络中，我们通常使用它来初始化偏置，以确保它们的初始值为零。
np.dot：这是一个用于进行矩阵相乘的函数。在神经网络中，我们使用这个函数来计算不同层之间神经元的连接以及权重与输入数据之间的乘积。这有助于执行神经网络的前向传播和反向传播计算。

这些函数在神经网络的实现中非常有用，因为它们可以帮助我们进行随机初始化、初始化和数学运算，这些都是神经网络训练过程中的基本操作。

如何理解激活函数Sigmod?
它是一种用来处理神经网络中的数值的特殊函数。它的作用就像是一个开关，可以把输入的数值变成0到1之间的输出。
如果我们把一个大的数值输入 Sigmoid 函数，它会输出接近于1的值，就好像是 开关被打开 一样。而如果我们输入一个负数或者很小的数，它会输出接近于0的值，就好像是开关被关闭一样。

所以，Sigmoid 函数的作用是把输入的数值 转换成一个在0到1之间的数 ，这在神经网络中常用于控制神经元的激活状态。这个函数的特点是输出总是在0到1之间，有助于神经网络学习非常复杂的模式和信息。

为什么需要设置b1、b2偏置调整神经元激活阈值呢？
简单来说，偏置就像是神经元的调节器，它帮助神经元更好地理解和处理各种不同的数据。

有些数据可能需要更小的刺激才能激活神经元，而有些数据可能需要更大的刺激。偏置就像是用来调整神经元敏感度的工具，使神经网络可以更好地学习和理解各种不同类型的数据。所以，偏置是神经网络中非常重要的部分，它增加了网络的适应能力，帮助网络更好地解决各种问题。