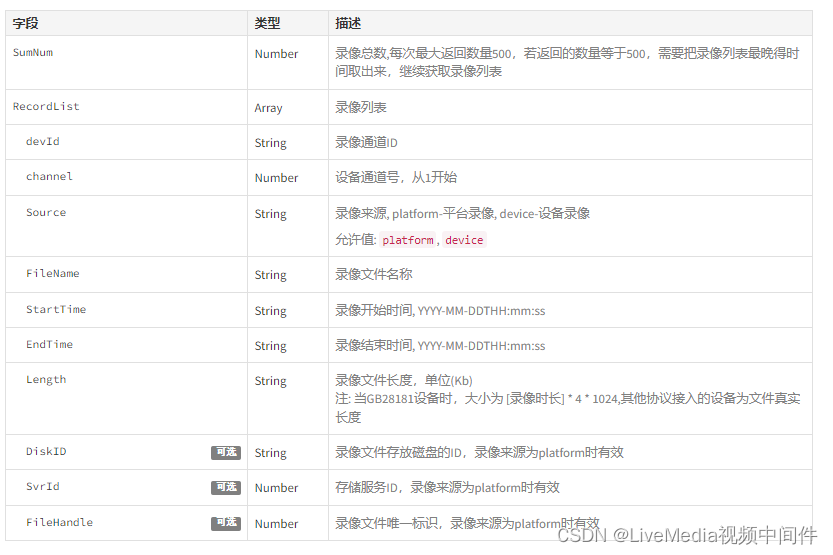
Artificial Intelligence 人工智能基本介绍

人工智能（Artificial Intelligence，AI）是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。它试图了解智能的实质，并生产出一种新的能以人类智能相似的方式做出反应的智能机器。人工智能的研究领域涵盖了机器人、语言识别、图像识别、自然语言处理和专家系统等。

人工智能是计算机科学的一个分支，它涉及到计算机科学、心理学、哲学和语言学等学科。可以说，人工智能几乎涉及到了自然和社会科学的所有学科，其范围已远远超出了计算机科学的范畴。

人工智能应用领域

人工智能发展必备三要素：数据、算法、计算力

首先，数据是人工智能发展的基础，包括海量的数据和高质量的数据。因为神经网络算法的层数为了达到良好效果，往往需要很多层，且参数量巨大，需要避免过拟合等问题，这些都需要海量的数据。没有足够的数据，即使有再好的算法也无法发挥其作用。

其次，算法是人工智能发展的核心，包括机器学习算法、深度学习算法等。算法本身的突破是人工智能发展的关键，因为只有好的算法才能够从海量的数据中提取出有价值的信息，进而实现智能化。

最后，计算力是人工智能发展的保障。随着数据量和算法复杂性的增加，人工智能需要更高的计算力来处理这些数据和算法。计算力包括硬件支撑和软件优化等方面，硬件支撑包括CPU和GPU等计算设备，软件优化则可以提高算法的执行效率和准确性。

总之，人工智能的发展需要数据、算法和计算力三个要素的共同作用。只有具备了这三个要素，才能够推动人工智能技术的不断进步和应用场景的不断拓展。

计算机中的两种重要处理器：CPU 和 GPU

CPU，也称为中央处理器或微处理器，是计算机的主要处理单元。它通过顺序执行指令来执行计算任务，并具有高度的灵活性，可以处理各种任务。CPU基于冯·诺依曼体系结构，包含控制单元、算术逻辑单元和缓存等部分。它通常用于诸如比特币挖矿、视频编辑等任务。

GPU，全称图形处理器，主要应用于图形处理和并行计算。基于数据流体系结构，GPU的并行计算能力是CPU的几倍甚至几十倍，可以处理大量的数据和计算任务。GPU设计目的是高效处理大规模并行计算和图形渲染，对于复杂的计算任务，如数据科学领域的分析程序，GPU能够提供更快的计算效率和速度。

总的来说，CPU和GPU各有其优点和缺点。CPU适合处理各种任务，具有高度的灵活性和高精度，而GPU则更适合处理大规模并行计算和图形渲染任务。

CPU：主要适合 I /O 密集型的任务
GPU：主要适合计算密集型任务

人工智能、机器学习、深度学习

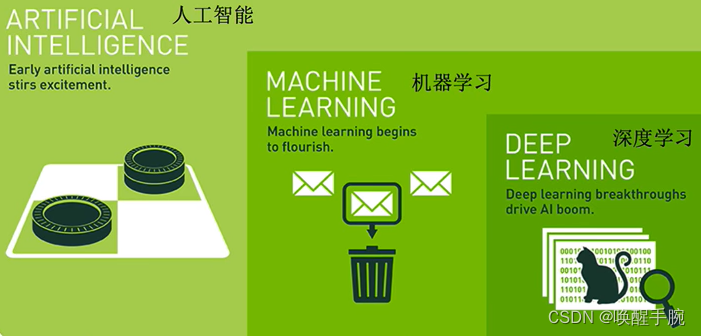
Machine Learning 机器学习基本概念

机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。它专门研究如何通过使用计算机模拟或实现人类学习行为，从而获取新的知识或技能，并重新组织已有的知识结构，以改善自身的性能。机器学习是人工智能的核心，是使计算机具有智能的根本途径。

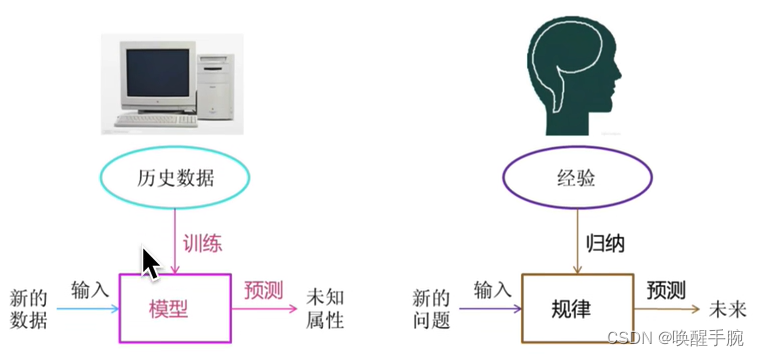
机器学习工作流程

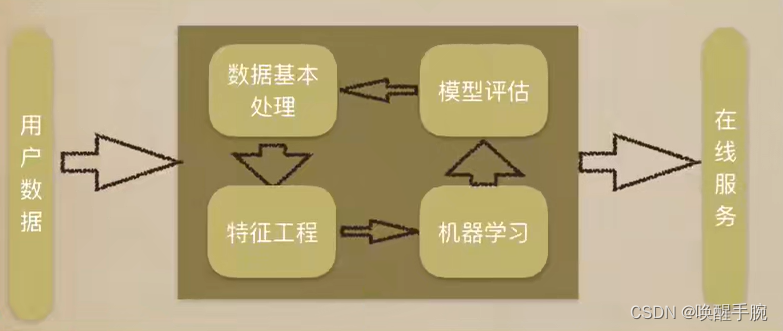
什么是特征工程？

特征工程是指将原始数据转换为更好地代表预测模型的潜在问题的特征的过程，从而提高了对未知数据的预测准确性。它包括特征构建、特征提取和特征选择三个部分，是机器学习中不可或缺的数据预处理和特征提取过程。

特征工程技术有哪些主要步骤？

数据探索：在任何数据分析和机器学习任务中，数据探索都是至关重要的第一步。它帮助我们理解数据的特性，确定是否存在缺失值或异常值，以及数据中可能存在的模式和趋势。
数据预处理：这是清理和准备数据的步骤，以便输入到模型中。它包括处理缺失值、异常值、离群值、错误和进行必要的类型转换。
特征构建：这个步骤通常涉及到从原始数据中创建新的特征。这可以通过各种方式实现，例如使用基本数学运算、计算统计量、文本处理等。
特征选择：这是一个从所有特征中选择最相关的特征的过程，以减少输入数据的维度并消除噪声。它有助于简化模型、提高效率，并可能改善模型的性能。
特征转换：在这个步骤，可能会使用一些数学或统计方法来转换已有的特征，以便更好地捕捉数据的结构或关系，或者提高模型的预测能力。
特征学习：这是一个使用特定算法从数据中学习有用特征的步骤。这通常涉及到神经网络或其他复杂的机器学习模型。

什么是监督学习？

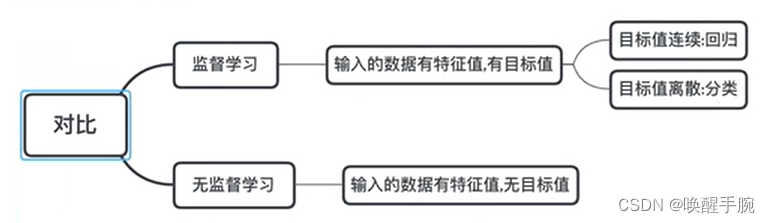
监督学习：线性回归、逻辑回归、决策树、神经网络（卷积神经网络、循环神经网络）
无监督学习：聚类算法

什么是强化学习？

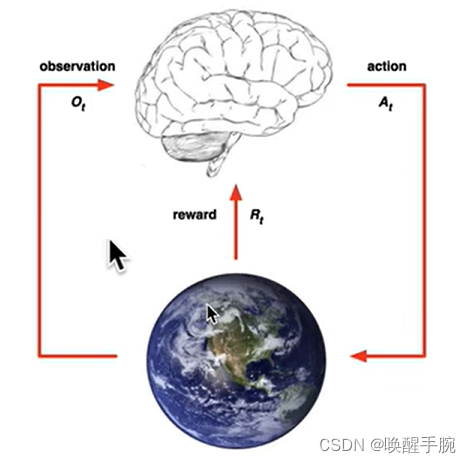
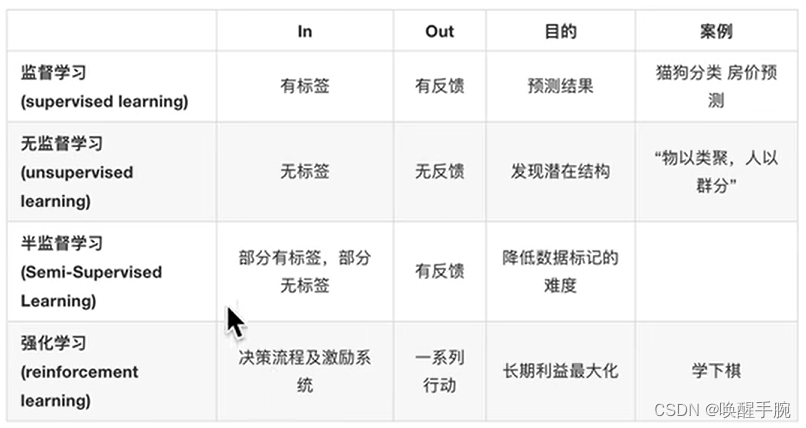
监督学习、无监督学习、半监督学习、强化学习

Model Evaluation 模型评估

模型评估（Model Evaluation）是检查模型在训练和测试数据集上的性能和效果的过程。模型评估的目的是了解模型是否能够有效地对新数据进行预测和分类。在模型评估中，通常会使用各种度量指标来评估模型的性能。

准确度（Accuracy）：衡量模型正确预测的比例。
精度（Precision）：衡量模型预测为正的样本中真正为正的比例。
召回率（Recall）：衡量模型正确找出正样本的比例。
F1分数（F1 Score）：综合考虑准确度和召回率，用来评估模型的整体性能。
ROC曲线（ROC Curve）：以假阳性率（False Positive Rate）为横轴，真阳性率（True Positive Rate）为纵轴绘制的曲线，用于评估模型的分类性能。
AUC值（Area Under Curve）：ROC曲线下的面积，衡量模型整体的分类性能。
交叉熵损失（Cross-Entropy Loss）：衡量模型预测与实际之间的差异。
在实际应用中，根据不同的任务和数据集，需要选择合适的评估指标。同时，为了更全面地评估模型性能，还可以进行多种评估指标的组合使用。

过拟合和欠拟合

欠拟合是指模型在训练集、验证集和测试集上均表现不佳的情况。这主要是由于学习不足造成的，具体可以通过增加特征、使用较复杂的模型，或者减少正则项来解决此问题。

过拟合是指模型在训练集上表现很好，到了验证和测试阶段就很差，即模型的泛化能力很差。这主要是由于模型复杂度过高，导致模型对训练数据过拟合，无法泛化到新的数据。

增加训练数据：这种方法可以增加模型的多样性和复杂性，从而降低过拟合的可能性。
简化模型：可以通过减少模型的复杂度，如减少神经网络的隐藏层数和隐藏单元数等，来降低过拟合。
正则化：正则化是一种通过在损失函数中添加一项，来惩罚模型的复杂度的方法。它的主要作用是避免模型学习过多的细节，从而降低过拟合。常用的正则化项包括L1正则和L2正则等。
早停法：这种方法是指在训练过程中，监视模型在验证集上的性能，当模型的验证性能开始下降时，就停止模型的训练。这样可以避免模型对训练数据过拟合。

Linear Regression 线性回归

线性回归是利用数理统计中的回归分析来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。它可以分为一元线性回归分析和多元线性回归分析，前者只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示；后者则包括两个或两个以上的自变量，且因变量和自变量之间是线性关系。

拟合的平面：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$（假设 ${\theta }_1$ 是年龄的参数；${\theta }_2$ 是工资的参数）

hypotheses function 假设函数

$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\dots +{\theta }_n{x}_n$

损失函数（Loss Function）和代价函数（Cost Function）在机器学习和人工智能领域中都是用来衡量模型预测误差的函数。

Loss Function 损失函数

损失函数是定义在单个样本上的，用于衡量一个样本的误差。它的主要应用场景包括回归问题和分类问题。对于回归问题，损失函数通常用来衡量预测值与真实值之间的差距，例如平方损失函数是将预测值和真实值相减然后平方。对于分类问题，损失函数则衡量的是预测分类错误的情况，例如铰链损失函数只有在预测完全正确时才为0，否则为1。

在线性回归中，一个常用的损失函数是平方损失函数（quadratic loss function），其表达式为：

$L(y,f(x))=(y-f(x){)}^2$

其中，$y$ 是实际值，$f(x)$ 是预测值。平方损失函数的特点是，预测值与实际值差的平方越大，损失也越大。它经常被应用在回归问题上。

Cost Function 代价函数

代价函数是定义在整个训练集上的，是所有样本误差的平均，也就是所有损失函数值的平均。它代表的是所有样本的平均损失或风险。在机器学习模型的训练过程中，我们通常会选择代价函数作为优化的目标，通过最小化代价函数来优化模型参数。

$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h(x^{(i)},\theta )-y^{(i)})$$
J = m i n i m i z e { 1 2 m ∑ i = 1 m ( Y − Y t r u t h ) 2 } J=minimize\{\frac{1}{2m}\sum_{i=1}^{m}(Y-Y_{truth} )^2\} J=minimize{2m1​i=1∑m​(Y−Ytruth​)2}