！经典DP！
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果 两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：
输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：
输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400

动态规划的的四个解题步骤是：

1. 定义子问题： 总问题：抢N个房子 – > 子问题：抢 K个房子

2. 写出子问题的递推关系：第k个房子要么被抢要么不被抢：F(k) = max(F(k-1), nums[k] + F(k-2))
   (只与前两个房子的最大金额有关——空间优化，N长数组变成2个变量)

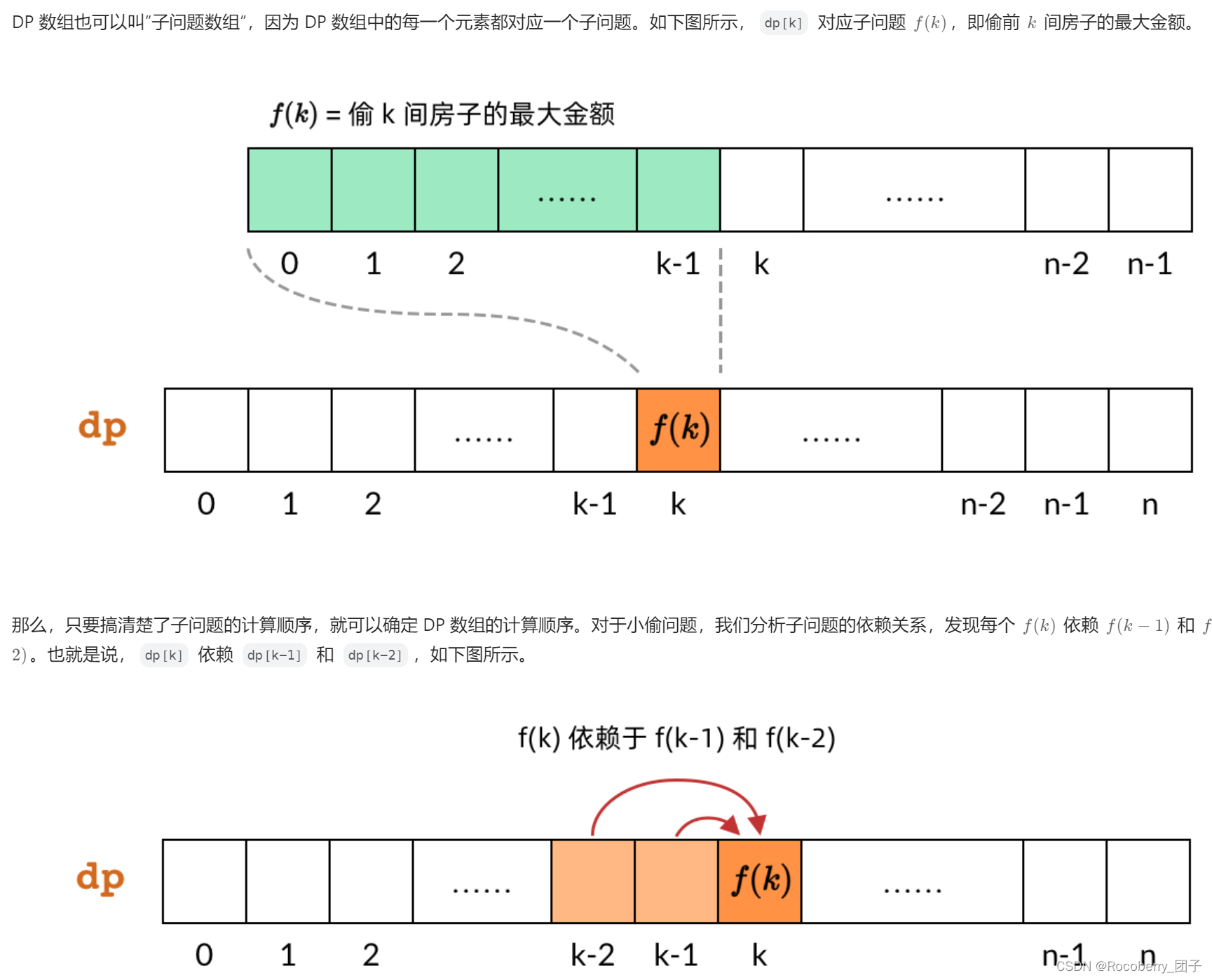
3. 确定 DP 数组的计算顺序：
   动态规划有两种计算顺序，一种是自顶向下的、使用备忘录的递归方法，一种是自底向上的、使用 dp 数组的循环方法。不过在普通的动态规划题目中，99% 的情况我们都不需要用到备忘录方法，所以我们最好坚持用自底向上的 dp 数组
   DP 数组中的依赖关系都是向右指的，DP 数组的计算顺序就是从左向右。这样我们可以保证，计算一个子问题的时候，它所依赖的那些子问题已经计算出来了。
   

4. 空间优化（可选）

题解1 DP1

class Solution {
public:int rob(vector<int>& nums) {int s = nums.size();vector<int> dp(s+1, 0);dp[1] = nums[0];for(int i = 1; i < s; i++){dp[i+1] = max(dp[i], dp[i-1]+nums[i]);}return dp[s];}
};

题解2 DP2

class Solution {
public:int rob(vector<int>& nums) {int s = nums.size();if(1 == s) return nums[0];int first = nums[0];int sec = max(nums[0], nums[1]);for(int i = 2; i < s; i++){int tmp = sec;// sec是i-1的情况， first是i-2sec = max(first+nums[i], sec);first = tmp;}return sec;}
};