视频：

https://www.bilibili.com/video/BV1CB4y1Z7kA

问题由来：

早期这个帖子里面的局部变量对齐仅测试了MDK AC5，但项目中使用AC6发现了新问题，看来AAPCS规约研究的还是不够细：

https://www.armbbs.cn/forum.php?mod=viewthread&tid=109400

当时对局部变量的描述如下：局部变量使用的是栈空间（除了静态局部变量和编译器优化不使用栈，直接用寄存器做变量空间），也就是大家使用在xxxx.S启动文件开辟的stack空间。

在M内核里面，局部变量的对齐问题如果研究起来是最烧脑的，这个涉及到AAPCS规约(Procedure Call Standard for the Arm Architecture,  Arm架构的程序调用标准)。

上面这个贴图最重要，仅需理解上面这两条就可以，意思是说，栈地址是全程至少保持4字节对齐的，因为M内核的硬件长做了处理，SP最低两个bit，bit0和bit1直接固定为0了。

但是在程序调用入口处必须满足8字节对齐，对于C语言，不需要用户去管，编译器都帮我们处理好了，先来个简单的示例压压惊：

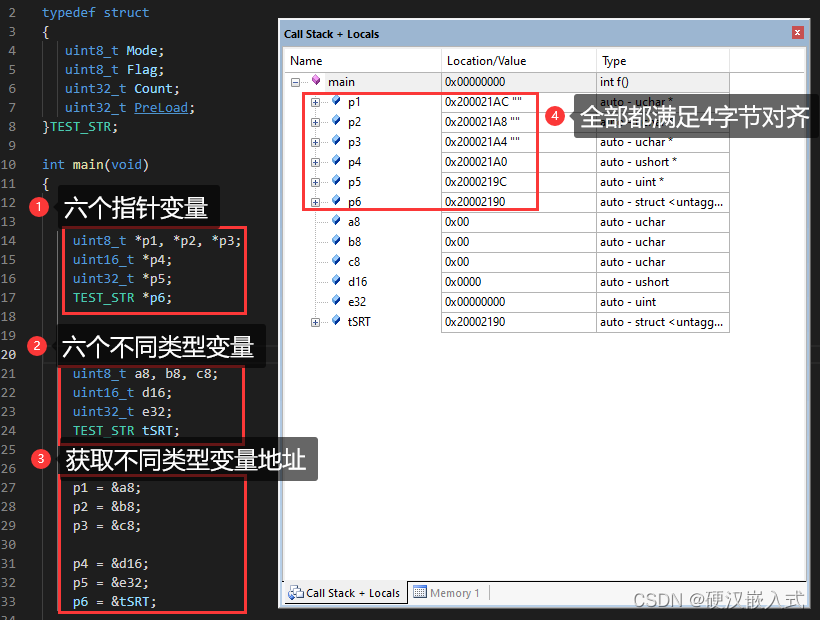
而汇编文件是需要用户去处理的。以xxx.S启动文件为例，通过伪指令PRESERVE8来保证

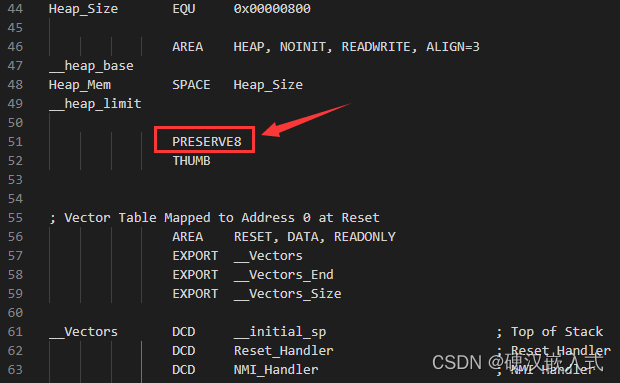
那么问题来了，我们搞个4对齐是不是会出问题，一般情况下也没问题的，但特殊情况下不行，特别调用C库的sprintf和printf函数，直接给你输出个不知所以然的结果来。比如我在H7上做如下测试：

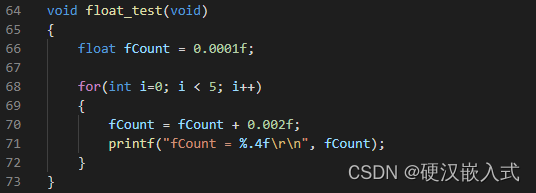
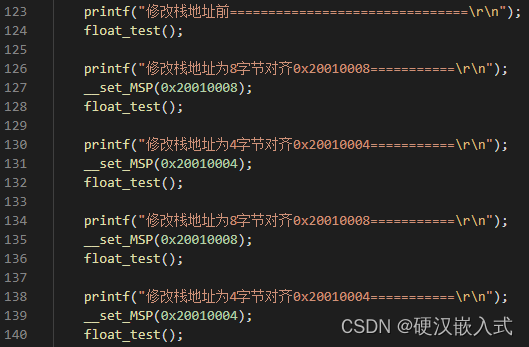
输出结果：

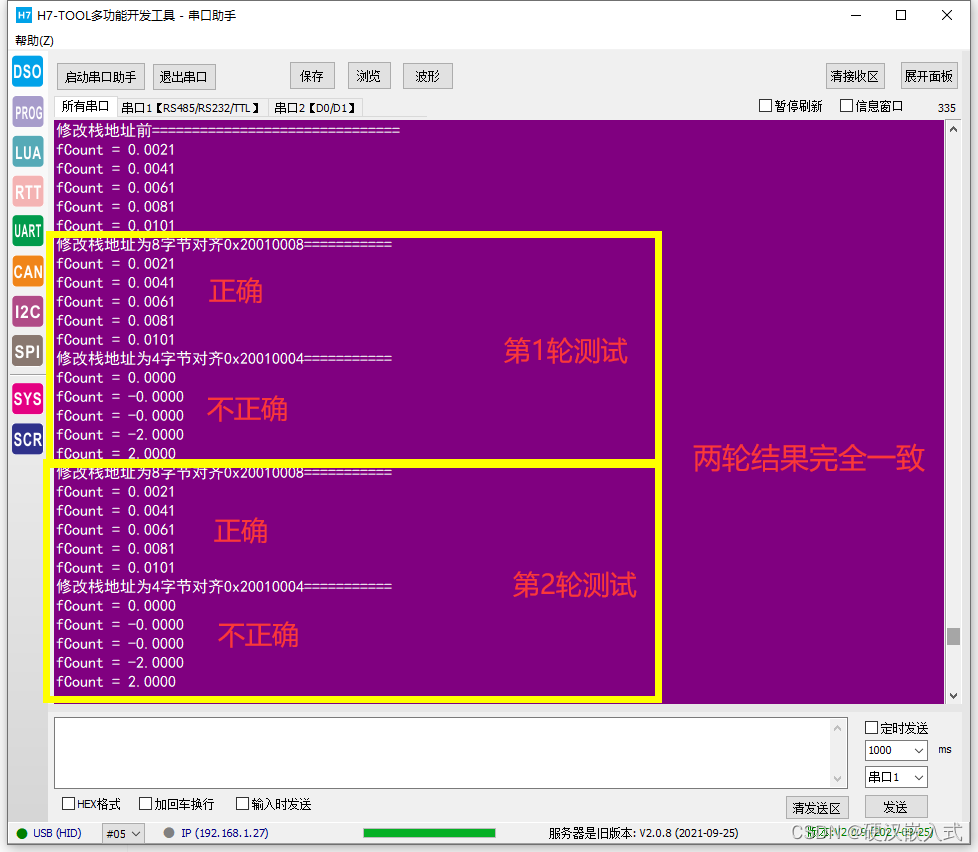
总结：

MDK AC5和IAR的用法差不多，MDK AC6和GCC的用法差不多视频里面做了详细对比测试）。

对于GCC和MDK AC6，大家可以手动添加__ALIGNED()设置对齐，这个原定义在CMSIS软件的头文件里面。

#define __ALIGNED(x)                           __attribute__((aligned(x)))

AC6定义如下：

#define __ALIGNED(x)                           __attribute__((aligned(x)))