本章讲解强化学习的基本概念。第 3.1 节介绍马尔可夫决策过程（Markov decision
process，简称 MDP），它是最常见的对强化学习建模的方法。第 3.2 节定义策略函数，包括随机策略和确定策略。第 3.3 节分析强化学习中的随机性的两个来源。第 3.4 节定义回报和折扣回报。第 3.5 节定义动作价值函数和状态价值函数。第 3.6 节介绍强化学习常用的实验环境。

3.1马尔科夫决策过程

强化学习的主体被称为智能体 (agent)。
环境（environment） 是与智能体交互的对象

强化学习的数学基础和建模工具是马尔可夫决策过程（Markov decision process， MDP）。一个 MDP 通常由状态空间、动作空间、状态转移函数、奖励函数、折扣因子等组成。

在每个时刻，环境有一个状态 (state)，可以理解为对当前时刻环境的概括。

• 状态空间（state space） 是指所有可能存在状态的集合，记作花体字母𝓢。

• 动作（action） 是智能体基于当前状态所做出的决策。

• 动作空间（action space） 是指所有可能动作的集合，记作花体字母 𝓐。

• 奖励（reward） 是指在智能体执行一个动作之后，环境返回给智能体的一个数值。

• 

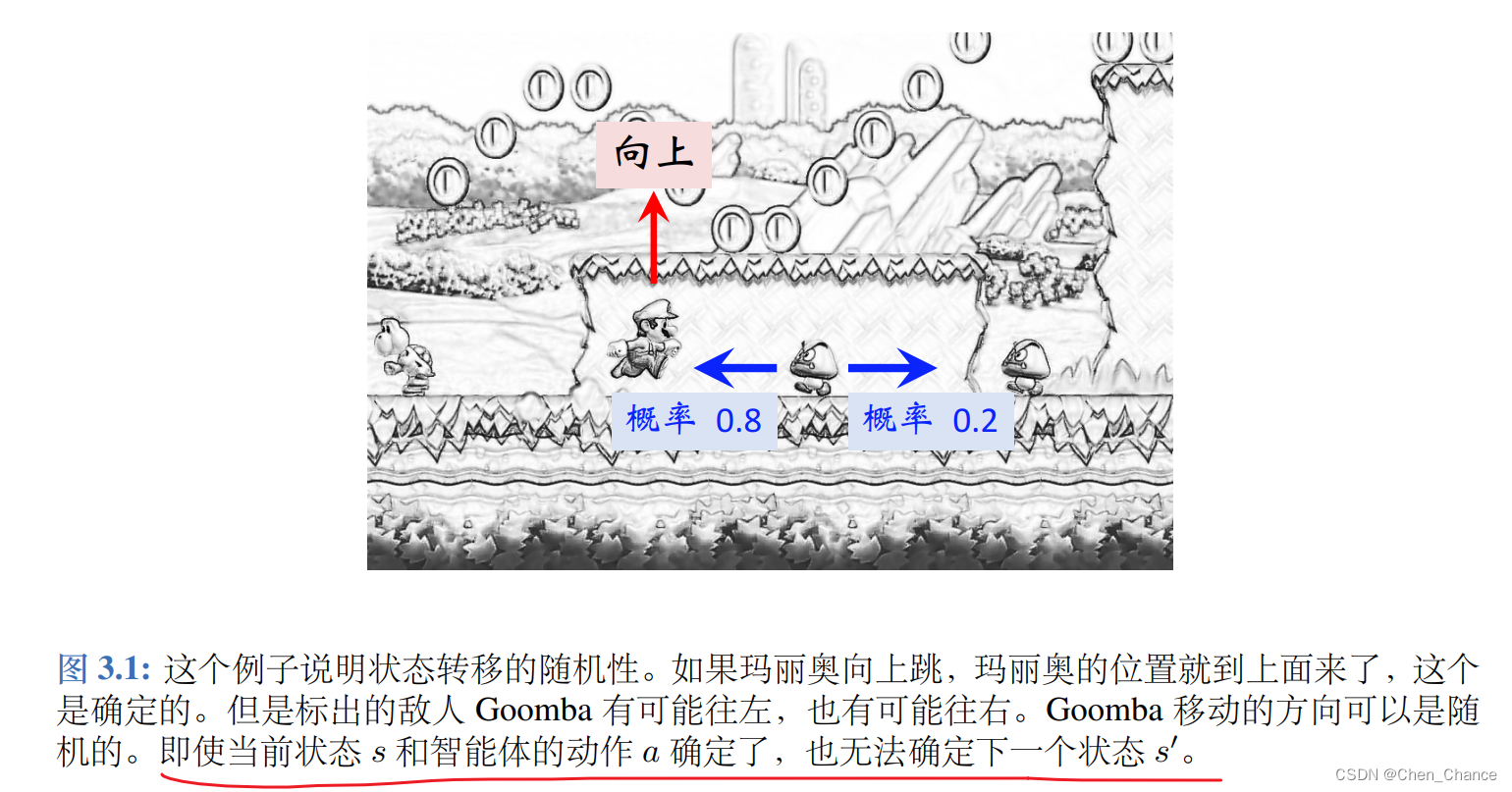
• 状态转移（state transition） 是指智能体从当前 t 时刻的状态 s 转移到下一个时刻状态为 s′ 的过程。

• 
  

3.2策略

策略（policy） 的意思是根据观测到的状态，如何做出决策，即如何从动作空间中选
取一个动作。
强化学习的目标就是得到一个策略函数，在每个时刻根据观测到的状态做出决策。

随机策略

确定策略

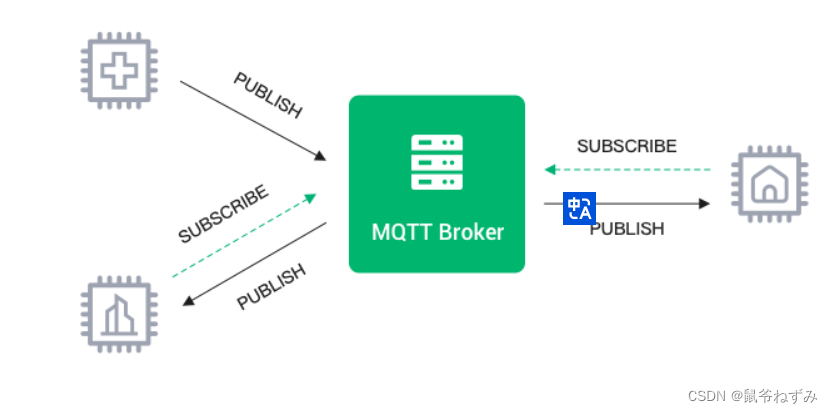
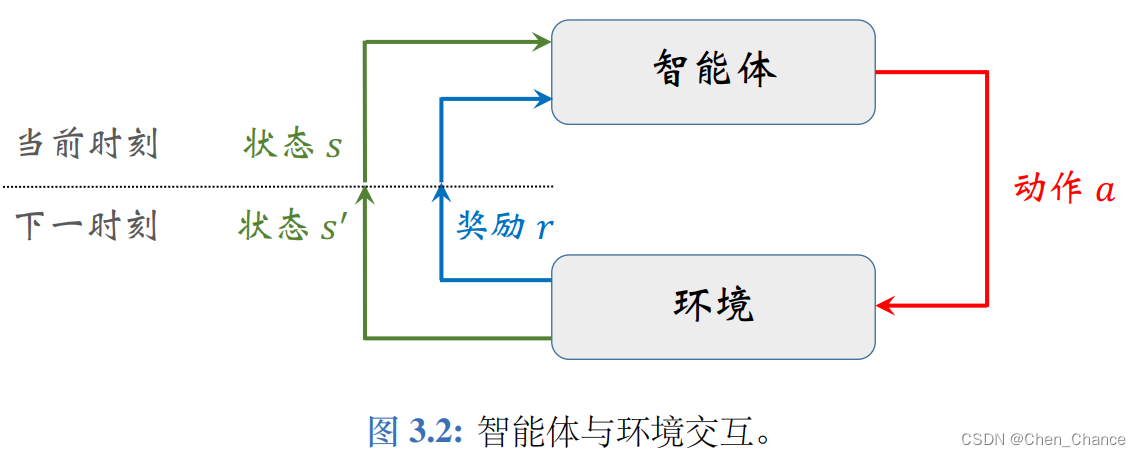
智能体与环境交互（agent environment interaction）

是指智能体观测到环境的状态s，做出动作 a，动作会改变环境的状态，环境反馈给智能体奖励 r 以及新的状态 s′。

回合（episodes）

“回合”的概念来自游戏，指智能体从游戏开始到通关或者结束的过程。强化学习对样本数量的要求很高，即便是个简单的游戏，也需要玩上万回合游戏才能学到好的策略。

Epoch 是一个类似而又有所区别的概念，常用于监督学习。一个 epoch 意思是用所有训练数据进行前向计算和反向传播，而且每条数据恰好只用一次。

3.3随机性的来源

这一节的内容是强化学习中的随机性。随机性有两个来源：策略函数与状态转移函数。搞明白随机性的两个来源，对之后的学习很有帮助。本书中用 $S_t$ 和 $s_t$ 分别表示 t 时刻的状态及其观测值，用 $A_t$ 和$a_t$ 分别表示 t 时刻的动作及其观测值。

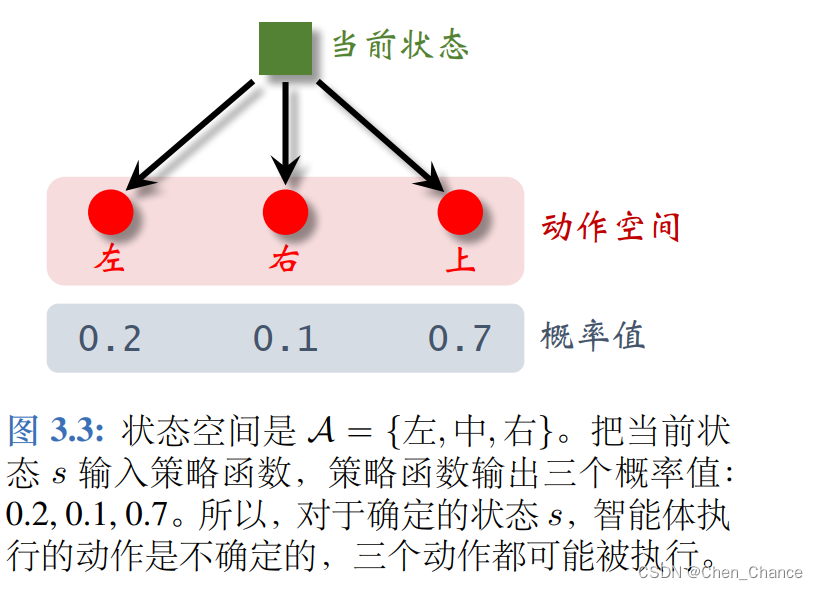
动作的随机性来自于随机决策。给定当前状态 s，策略函数 $\pi (a|s)$ 会算出动作空间 A 中每个动作 a 的概率值。智能体执行的动作是随机抽样的结果，所以带有随机性。

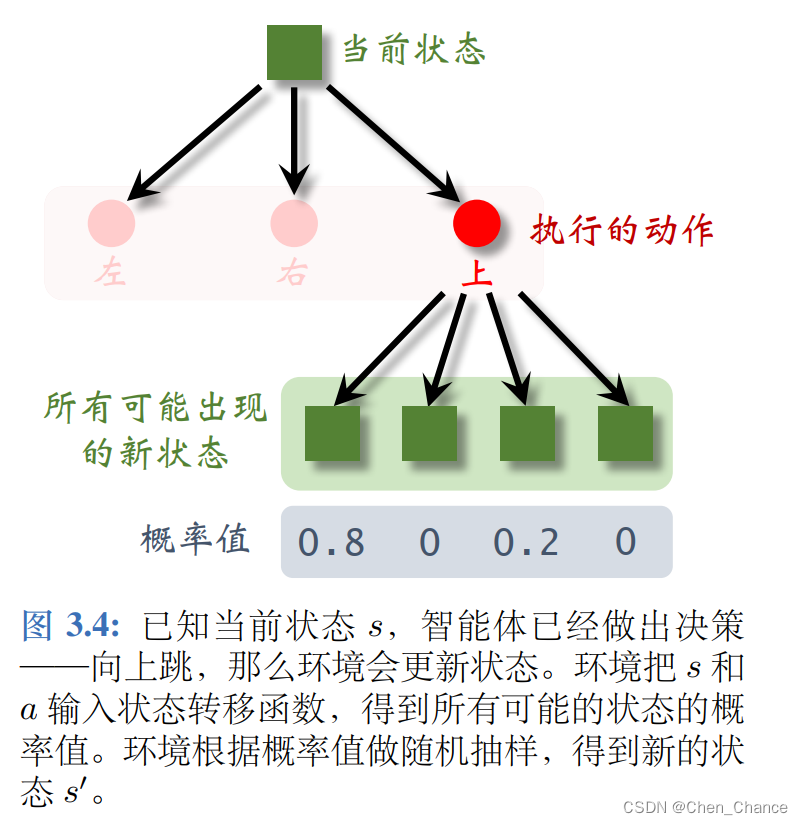
状态的随机性来自于状态转移函数。当状态 s 和动作 a 都被确定下来，下一个状态仍然有随机性。环境（比如游戏程序）用状态转移函数 p(s′|s, a) 计算所有可能的状态的概率，然后做随机抽样，得到新的状态。

奖励是状态和动作的函数。
$r_t=r(s_t,a_t).$
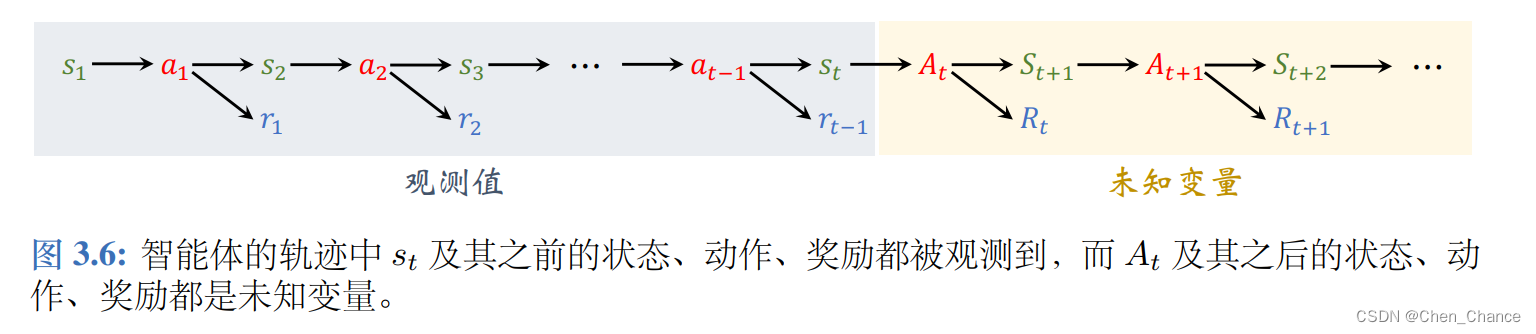
如果 At 还没被观测到，或者 (St, At) 都没被观测到，那么 t 时刻的奖励就有不确定性。我们用
$R_t=r(s_t,A_t)$或$R_t=r(S_t,A_t)$

马尔可夫性质（Markov property）︒ 上文在讲解状态转移的时候，假设状态转移具有马尔可夫性质，

轨迹（trajectory） 是指一回合（episode）游戏中，智能体观测到的所有的状态、动作、奖励：

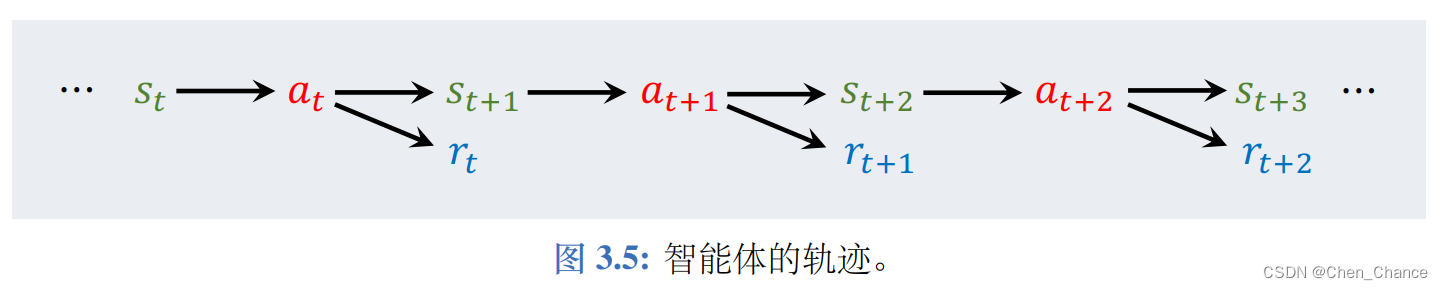
3.4回报与折扣回报

本节介绍回报（return）和折扣回报（discounted return）这两个概念，并且讨论其随机性来源。由于回报是折扣率等于 1 的特殊折扣回报，后面的章节中用“回报”指代“折扣回报”，不再区分两者。本节我们用 Rt 和 rt 表示 t 时刻奖励随机变量及其观测值

3.4.1回报

回报（return） 是从当前时刻开始到本回合结束的所有奖励的总和，所以回报也叫做累计奖励（cumulative future reward） 。

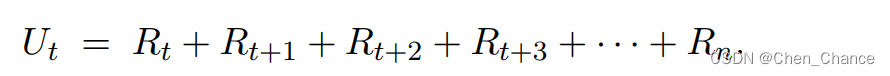
强化学习的目标是最大化回报，而不是最大化当前的奖励。

3.4.2 折扣回报

3.4.3 回报中的随机性

3.4.4 有限期 MDP 和无限期 MDP

本书后面章节统一用 n 表示回合的长度。方便起见，我们就不再严格区分有限期和无限期的情况，即不区分 n 是有界、还是 n→∞。

3.5价值函数

这一节介绍动作价值函数$Q_{\pi }(s,a)$，最优动作价值函数$Q_{\star }(s,a)$，状态价值函数$V_{\pi }(s)$。它们都是回报的期望。

3.5.1 动作价值函数

在 t 时刻，我们不知道 $U_t$ 的值，而我们又想预判 Ut 的值从而知道局势的好坏。该怎么办呢？解决方案就是对 Ut 求期望，消除掉其中的随机性。


上文这里我纠结了很久为什么也依赖于状态s_t而只说a_t的作用，后来转念一想，只是说依赖于没有说只依赖于，所以就不纠结了（也有可能我理解有误）

（补充：更准确地说，应该叫“动作状态价值函数”，但是大家习惯性地称之为“动作价值函数”。这可能和我上面的纠结遥相呼应）

3.5.2 最优动作价值函数

3.5.3 状态价值函数

假设 AI 用策略函数 π 下围棋。 AI 想知道当前状态 $s_t$（即棋盘上的格局）是否对自己有利，以及自己和对手的胜算各有多大。该用什么来量化双方的胜算呢？答案是状态价值函数（state-value function）

3.6实验环境

如果你设计出一种新的强化学习方法，你应该将其与已有的标准方法做比较，看新的方法是否有优势。比较和评价强化学习算法最常用的是 OpenAI Gym，它相当于计算机视觉中的 ImageNet 数据集。 Gym 有几大类控制问题，比如经典控制问题、 Atari 游戏、机器人。

• Gym 中第一类是经典控制问题，都是小规模的简单问题，比如 Cart Pole 和 Pendulum
  Cart Pole 和 Pendulum 都是典型的无限期 MDP，即不存在终止状态。
  
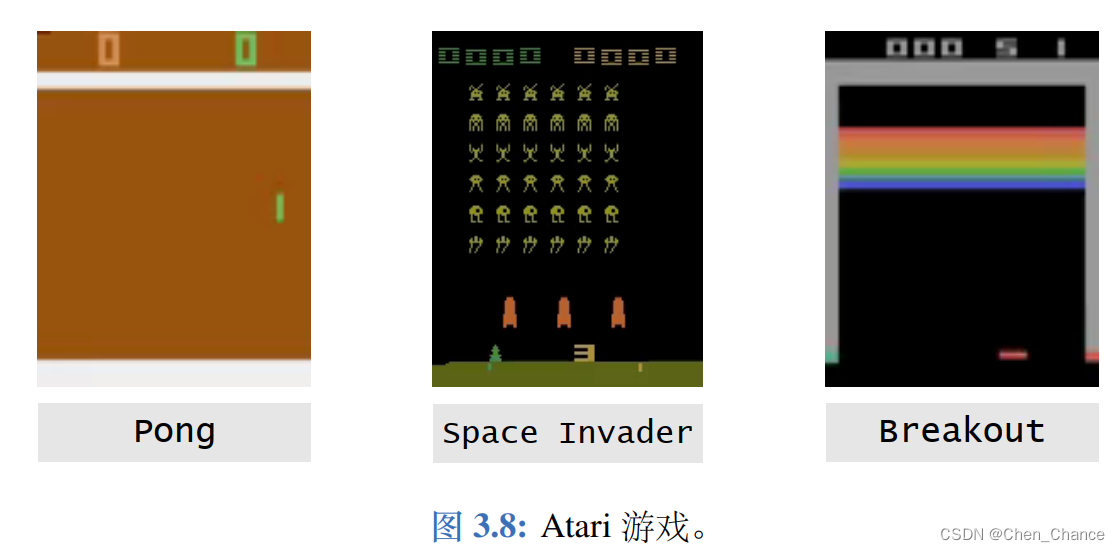
• 第二类问题是 Atari 游戏，就是八、九十年代小霸王游戏机上拿手柄玩的那种游戏
  Atari 游戏大多是有限期 MDP，即存在一个终止状态，一旦进入该状态，则游戏会终止。
  
• 第三类问题是机器人连续的控制问题，比如控制蚂蚁、人、猎豹等机器人走路