1 网络社区挖掘定义
网络社区挖掘是指利用数据挖掘技术和机器学习算法,分析社交网络、在线社区或互联网上的各种交互数据,以揭示其中隐藏的模式、关系和信息。这些社区可以是社交媒体平台、在线论坛、博客、微博等,人们在这些平台上进行交流、分享信息和建立连接。
通常包含:
-
社区发现(Community Detection): 识别社交网络中具有紧密连接的群体,帮助了解社区结构和成员之间的关系。
-
信息传播分析(Information Diffusion Analysis): 研究在社交网络中信息是如何传播和扩散的,以及影响传播的因素。
-
用户行为分析(User Behavior Analysis): 分析用户在网络社区中的行为,包括发帖、评论、点赞等,以了解用户兴趣和行为模式。
-
情感分析(Sentiment Analysis): 分析社交网络中文本数据的情感色彩,了解用户对特定话题或事件的情感倾向。
-
影响力分析(Influence Analysis): 确定社交网络中具有影响力的个体,可以是个人、组织或事件,了解他们对社区的影响程度。
2 图论的基本知识
网络社区挖掘,离不开图论知识,这属于笔者的知识盲区,不得不补充学习,如下列出基本的知识架构图。
2.1 基本概念
2.1.1 图的定义: 节点(顶点)和边的集合。
图(Graph)是由节点(顶点)和连接这些节点的边(或弧)组成的数学结构
图可以用数学表示,例如,一个图可以用G=(V, E)表示,其中V是节点的集合,E是边的集合。
- 节点(顶点)(V): 图中的基本单元,通常用来表示实体或对象。
- 边(Edge)(E): 连接图中两个节点的线段,用来表示节点之间的关系。边可以是有向的(箭头表示方向)或无向的(没有方向)。
- 有向图(Directed Graph): 图中的边有方向性,即从一个节点到另一个节点有一个确定的方向
- 无向图(Undirected Graph): 图中的边没有方向性,即连接两个节点的边没有起点和终点之分。
- 简单图(Simple Graph): 无自环(节点没有与自身相连的边)且无重边(同一对节点之间最多只有一条边)的图。
- 多重图(Multigraph): 允许两个节点之间有多条边的图。
- 自环(Loop): 连接节点和其自身的边。
- 子图(Subgraph): 图G的子集,包括G的一些节点和边,且这些边的两个端点都在子图中。
- 完全图(Complete Graph): 所有节点之间都有边相连的图。
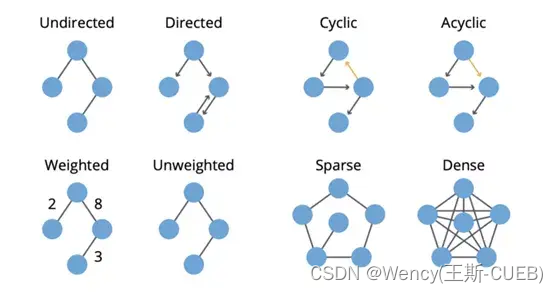
2.1.2 图的类型: 无向图、有向图、加权图、带标签图等。
图的来源:
【图论与图学习(一):图的基本概念】
- 无向图(Undirected Graph):
定义: 图中的边没有方向,即连接两个节点的边没有起点和终点之分。
解释: 无向图中的边表示两个节点之间的双向关系,信息在节点之间可以双向传递。 - 有向图(Directed Graph):
定义: 图中的边有方向性,即从一个节点到另一个节点有一个确定的方向。
解释: 有向图中的边有明确的方向,表示了一种单向关系,信息在节点之间只能按照边的方向传递。 - 加权图(Weighted Graph):
定义: 图中的边具有权重(权值),表示连接两个节点的边的强度、成本或距离。
解释: 加权图用于表示实际问题中的带权关系,例如网络中的通信成本、道路网中的距离等。 - 带标签图(Labeled Graph):
定义: 图中的节点或边带有标签或标识,用于表示节点或边的特定属性或信息。
解释: 带标签的图可用于表示网络中的实体具有特定特征,或者用于在图上附加额外的信息,例如在社交网络中标记不同用户的兴趣爱好。 - 多重图(Multigraph):
定义: 允许两个节点之间有多条边的图,即图中可能存在多条连接同一对节点的边。
解释: 多重图允许在同两个节点之间建立多种关系,用于表示不同性质的连接关系。 - 无向完全图(Complete Undirected Graph):
定义: 任意两个不同节点之间都有且仅有一条边连接的无向图。
解释: 无向完全图中的每对节点之间都存在边,表示了一种高度密集的关系。 - 有向完全图(Complete Directed Graph):
定义: 任意两个不同节点之间都有两条边,一条指向另一个节点,一条反向指向的有向图。
解释: 有向完全图中的每对节点之间都存在正向和反向两条边,表示了一种高度密集的单向关系。
2.1.3 度数: 节点的连接数。
无向图中的度数: 无向图中节点的度数是指与该节点相连的边的数量。例如,如果一个无向图中的节点A连接着3条边,那么节点A的度数就是3。
有向图中的入度和出度:
- 入度(In-Degree): 有向图中,一个节点收到的边的数量称为入度。入度表示有多少条边指向该节点。
- 出度(Out-Degree): 有向图中,一个节点发出的边的数量称为出度。出度表示该节点有多少条边指向其他节点。
2.1.4 路径和环: 路径是节点序列,环是起点和终点相同的路径。
-
路径(Path): 在图中,路径是指图中的节点按照边的连接顺序形成的序列。路径是一个节点序列,其中路径上的相邻节点由图中的边连接。路径可以是简单路径,即路径上的节点不重复;或者是通路(Trail),允许节点和边重复。
-
环(Cycle): 环是一种特殊的路径,它形成一个回路,即路径的起点和终点相同。环是一个简单路径,除了起点和终点相同之外,路径上的其他节点不重复。
举个例子,考虑一个简单无向图,其中的节点为A、B、C、D,边为{A, B}、{B, C}、{C, D}、{D, A}。在这个图中:
A到B再到C形成了一个路径:A -> B -> C。
A到B再到C再到D再回到A形成了一个环:A -> B -> C -> D -> A。
2.2 图的表示
2.2.1 邻接矩阵和邻接表: 不同的方法来表示图的结构。
邻接矩阵(Adjacency Matrix):
邻接矩阵是一个二维数组,用来表示图中的节点之间的连接关系。对于一个有N个节点的图,邻接矩阵是一个N × N的矩阵,其中的元素 a [ i ] [ j ] a[i][j] a[i][j]表示节点i和节点j之间是否有边连接。如果有连接,则a[i][j]的值通常为1(或者其他非零值,具体取决于问题的要求);如果没有连接,则a[i][j]的值为0。
优势:
对于稠密图(边数接近节点数的平方),邻接矩阵是一种非常高效的表示方法,因为大部分元素为0,节省了存储空间。
可以快速判断两个节点之间是否有边直接相连,时间复杂度为 O ( 1 ) O(1) O(1)。
劣势:
对于稀疏图(边数远小于节点数的平方),邻接矩阵会浪费大量的空间,因为大部分元素为0。
插入或删除边的操作相对较慢,需要更新整个矩阵。
邻接表(Adjacency List):
邻接表是一种以链表形式存储图的表示方法。对于每个节点,用一个链表(或数组)存储与该节点直接相连的所有节点。
优势:
对于稀疏图,邻接表是一种非常高效的表示方法,因为它只存储了实际存在的边,节省了存储空间。
插入或删除边的操作相对较快,只需要更新相关链表。
劣势:
对于密集图,邻接表可能会占用较多的空间,因为它需要存储大量的链表头和指针。
判断两个节点之间是否有边需要遍历链表,时间复杂度取决于链表长度。
选择邻接矩阵还是邻接表通常取决于图的密度和具体的应用需求。在实际应用中,程序员和算法设计者根据问题的特性来选择适合的表示方法。
2.2.1 关联矩阵: 用于有向图的表示。
关联矩阵(Incidence Matrix)是用于有向图的一种表示方法,它将图中的节点和边关系映射到一个二维矩阵中。对于一个有向图,关联矩阵的行代表节点,列代表边,矩阵中的元素表示节点与边的关系。通常,关联矩阵中的元素可以是1、-1或0,具体取决于图的方向。
- 如果节点i是边j的起始节点,则在矩阵中, a [ i ] [ j ] = 1 a[i][j] = 1 a[i][j]=1。
- 如果节点i是边j的结束节点,则在矩阵中, a [ i ] [ j ] = − 1 a[i][j] = -1 a[i][j]=−1。
- 如果节点i与边j没有关系,则在矩阵中, a [ i ] [ j ] = 0 a[i][j] = 0 a[i][j]=0。
例子:
假设有一个有向图如下:

| 1 | 2 | 3 | |
|---|---|---|---|
| A | 1 | -1 | 0 |
| B | -1 | 0 | 1 |
| C | 0 | 1 | -1 |
| D | 0 | 0 | -1 |
在这个关联矩阵中,行代表节点(A、B、C、D),列代表边(1、2、3),矩阵中的元素表示节点与边的关系。
以下东西属于代码部分,只做简单提要======================================================================================================================================================================
2.3 图的遍历
2.3.1 深度优先搜索(DFS): 递归或栈的方式。[伪代码]
递归
DFS(node):if node is not visited:Mark node as visitedProcess(node)for each neighbor in neighbors of node:if neighbor is not visited:DFS(neighbor)栈
DFS(startNode):stack = new Stack()stack.push(startNode)while stack is not empty:currentNode = stack.pop()if currentNode is not visited:Mark currentNode as visitedProcess(currentNode)for each neighbor in neighbors of currentNode:if neighbor is not visited:stack.push(neighbor)一般来说,递归调用比较吃内存,DFS一般使用栈方式
2.3.2 广度优先搜索(BFS): 队列的方式。[伪代码]
广度优先搜索(Breadth-First Search,BFS)是一种图遍历算法,它从起始节点开始,逐层地向外扩展,先访问离起始节点最近的节点,然后是离起始节点更远的节点。BFS通常使用队列(Queue)来辅助实现,保证节点的访问顺序是按照距离递增的顺序进行的。
BFS(startNode):queue = new Queue()queue.enqueue(startNode)mark startNode as visitedwhile queue is not empty:currentNode = queue.dequeue()process currentNodefor each neighbor in neighbors of currentNode:if neighbor is not visited:queue.enqueue(neighbor)mark neighbor as visited在这个算法中,队列保证了节点的访问顺序,先进先出(FIFO)的特性使得离起始节点近的节点优先被访问,从而实现了广度优先的遍历。
2.3.3 广度优先搜索(BFS) VS 深度优先搜索 (DFS)
-
- 遍历顺序的不同:
BFS(广度优先搜索): 从起始节点开始,逐层地向外扩展。首先访问离起始节点最近的节点,然后是离起始节点更远的节点。
DFS(深度优先搜索): 从起始节点开始,沿着一条分支尽可能深地访问,直到无法继续为止,然后回溯到上一个节点,再继续访问其他分支。
- 遍历顺序的不同:
-
- 数据结构的不同:
BFS: 使用队列(Queue)作为辅助数据结构,保证了节点的访问顺序是按照距离递增的顺序进行的。
DFS: 可以使用递归调用或者栈(Stack)作为辅助数据结构,递归实现时利用函数调用栈,栈实现时手动管理节点的访问顺序。
- 数据结构的不同:
-
- 空间复杂度:
BFS: 在最坏情况下,BFS需要存储所有节点,因此空间复杂度较高,特别是在处理大规模图时。
DFS: 在DFS的递归实现中,系统会自动维护函数调用栈,所以空间复杂度相对较低。但在处理深度较大的分支时,递归深度可能较大,有可能引发栈溢出。
- 空间复杂度:
-
- 应用场景:
BFS: 适用于寻找最短路径,例如在无权图中寻找最短路径,以及在树或图中寻找层级关系。
DFS: 适用于寻找所有可能的路径,例如在图中寻找所有的路径,以及在树中进行深度优先遍历。
- 应用场景:
-
- 完备性:
BFS: 由于其逐层扩展的特性,BFS能够找到最短路径(如果存在的话)。
DFS: DFS可能在无限循环的图中陷入,因此在应用中需要考虑避免重复访问,以及设置最大深度限制。
总结:一般情形下BFS优于DFS
- 完备性:
2.4 最短路径算法
2.4.1 狄克斯特拉算法(Dijkstra): 用于计算单源最短路径。
【没弄懂】 高质量传送门
2.4.2 贝尔曼-福德算法(Bellman-Ford): 用于处理带有负权边的图。
【没弄懂】高质量传送门
2.5 最小生成树
2.5.1 普里姆算法(Prim): 用于构建无向图的最小生成树。
传送门
2.5.2 克鲁斯卡尔算法(Kruskal): 用于构建无向图的最小生成树。
传送门
2.6 网络流
2.6.1 最大流最小割定理: 网络流问题的基本理论。
2.6.2 Ford-Fulkerson算法: 计算最大流的经典算法。
2.7图的匹配
2.7.1 二分图匹配: 匹配问题在二分图上的应用。
最大流最小割定理(Max-Flow Min-Cut Theorem)是网络流问题中的基本理论。它阐述了在一个网络流图中,最大流的值等于最小割的容量。这个定理揭示了网络流问题的一种非常重要的性质,对于解决网络流问题提供了关键指导。
-
最大流(Max-Flow): 一个网络流问题中,最大流是指从源节点到汇节点的最大流量。流量网络中的边都有一个最大容量,最大流问题的目标是找到一种合理的流量分配,使得从源节点到汇节点的流量达到最大。
-
最小割(Min-Cut): 一个割是指将网络节点分为两个不相交的子集,源节点在其中一个子集中,汇节点在另一个子集中。割的容量是指割中所有边的容量之和。最小割问题的目标是找到一种割,使得割的容量最小。
最大流最小割定理的关键在于,它指出了在网络流图中,最大流的值总是等于某个割的容量的最小值。这意味着,如果我们能够找到一个割,使得割的容量等于最大流的值,那么我们就找到了问题的最优解。在实际应用中,最大流最小割定理经常被用来求解网络流问题,包括网络设计、最优分配等问题。
2.7.2 匈牙利算法: 解决二分图最大匹配问题的算法。
匈牙利算法(Hungarian Algorithm)是一种用于解决二分图最大匹配问题的经典算法。在二分图中,匈牙利算法可以高效地找到最大的匹配,即在图中找到尽可能多的边,使得没有两条边有一个共同的顶点。
- 算法步骤:
初始化: 将所有的匹配标记为未完成,即所有边的状态为未匹配。
交替路径和增广路径: 通过交替路径(Alternating Paths)和增广路径(Augmenting Paths)来不断增加匹配。交替路径是指一条交替经过未匹配边和已匹配边的路径,增广路径是一条起始和结束都是未匹配顶点的交替路径。
增广路径的查找: 使用深度优先搜索(DFS)或广度优先搜索(BFS)等方法,在交替路径中查找增广路径。
路径更新: 找到增广路径后,根据该路径更新匹配,即将路径中的未匹配边变为已匹配,已匹配边变为未匹配。
重复步骤3和步骤4: 不断查找增广路径并更新匹配,直到无法找到新的增广路径为止。
- 算法特点:
最大匹配: 匈牙利算法能够找到二分图的最大匹配,即最大的边数,使得没有两条边有一个共同的顶点。
时间复杂度: 匈牙利算法的时间复杂度为O(V * E),其中V为顶点数,E为边数。在实际应用中,特别是对于稠密图,效率较高。
适用性: 匈牙利算法仅适用于二分图,即图中的节点可以划分为两个独立的集合,且边只能连接不同集合中的节点。
匈牙利算法在实际中广泛应用于任务分配、资源优化、稳定婚姻问题等领域,它提供了一种有效的方法来解决最大匹配问题。
2.8 图的颜色问题
2.8.1 图的着色问题: 最小顶点着色、最小边着色等问题。
图的着色问题是图论中的一个经典问题,主要研究如何用最少的颜色对图的顶点或边进行着色,使得相邻的顶点或边颜色不相同。这个问题有不同的变体,包括最小顶点着色、最小边着色等。
- 最小顶点着色问题(Vertex Coloring Problem):
最小顶点着色问题是指给定一个图,找到一种顶点着色方式,使得相邻的顶点具有不同的颜色,并且所需的颜色数目最少。这个问题的最优解称为图的色数(Chromatic Number)。
解决最小顶点着色问题的算法包括贪心算法、回溯算法等。贪心算法是一种常用的启发式方法,它从一个顶点开始,依次对每个未着色的顶点尝试分配最小的可用颜色,直到所有顶点都着色为止。
- 最小边着色问题(Edge Coloring Problem):
最小边着色问题是指给定一个图,找到一种边着色方式,使得相邻的边具有不同的颜色,并且所需的颜色数目最少。这个问题的最优解称为图的边色数(Chromatic Index)。
解决最小边着色问题的算法相对复杂,一种常见的方法是使用线性规划或者图论中的匈牙利算法。
-
应用领域:
图的着色问题在实际应用中具有广泛的应用,例如: -
调度问题: 在课程表、考试安排、航班调度等问题中,顶点代表事件,边代表冲突,最小顶点着色问题可以用于避免冲突。
-
频谱分配问题: 在无线通信领域,顶点代表基站,边代表干扰关系,最小顶点着色问题可以用于频谱分配,避免干扰。
-
任务调度问题: 在分布式系统中,顶点代表任务,边代表任务间的依赖关系,最小顶点着色问题可以用于分配资源,确保任务之间的依赖关系得到满足。
这些问题的解决对于提高资源利用率、减少冲突、提高系统效率等方面具有重要意义。
2.8.2 图的染色问题: 费用最小化问题,如涂色问题。
图的染色问题是图论中的一个经典问题,它通常涉及到将图的顶点或边用尽量少的颜色涂色,使得相邻的顶点或边颜色不相同。染色问题可以有多个变体,其中包括费用最小化问题,例如涂色问题。
-
涂色问题(Graph Coloring Problem):
涂色问题主要包括最小顶点着色问题和最小边着色问题,这两个问题都属于染色问题的一种。 -
最小顶点着色问题(Vertex Coloring Problem): 给定一个图,找到一种顶点着色方式,使得相邻的顶点具有不同的颜色,并且所需的颜色数目最少。
-
最小边着色问题(Edge Coloring Problem): 给定一个图,找到一种边着色方式,使得相邻的边具有不同的颜色,并且所需的颜色数目最少。
-
费用最小化问题(Cost Minimization Problem):
在染色问题中,有时候还需要考虑额外的约束条件,例如给不同的颜色赋予不同的权重或费用。费用最小化问题就是在染色的同时,要求满足某些额外的条件,例如最小化使用的颜色的总权重或费用。
这类问题通常可以转化为优化问题,并可以使用线性规划、动态规划等算法进行求解。在实际应用中,例如调度问题中,不同颜色的任务可能对应不同的执行时间或资源消耗,因此需要考虑最小化总体的执行时间或资源消耗。
染色问题及其相关的费用最小化问题在图论、图像处理、调度问题等领域都有广泛的应用。这些问题的解决有助于提高资源利用效率、降低成本等方面的优化。
------------------------------------------------------这部分不做叙述------------------------------------------------