门把手行业是指专门从事门把手的设计、制造、销售和安装等相关业务的行业。门把手是门窗装饰硬件的一种,用于开启和关闭门窗,同时也具有装饰和美化门窗的作用。
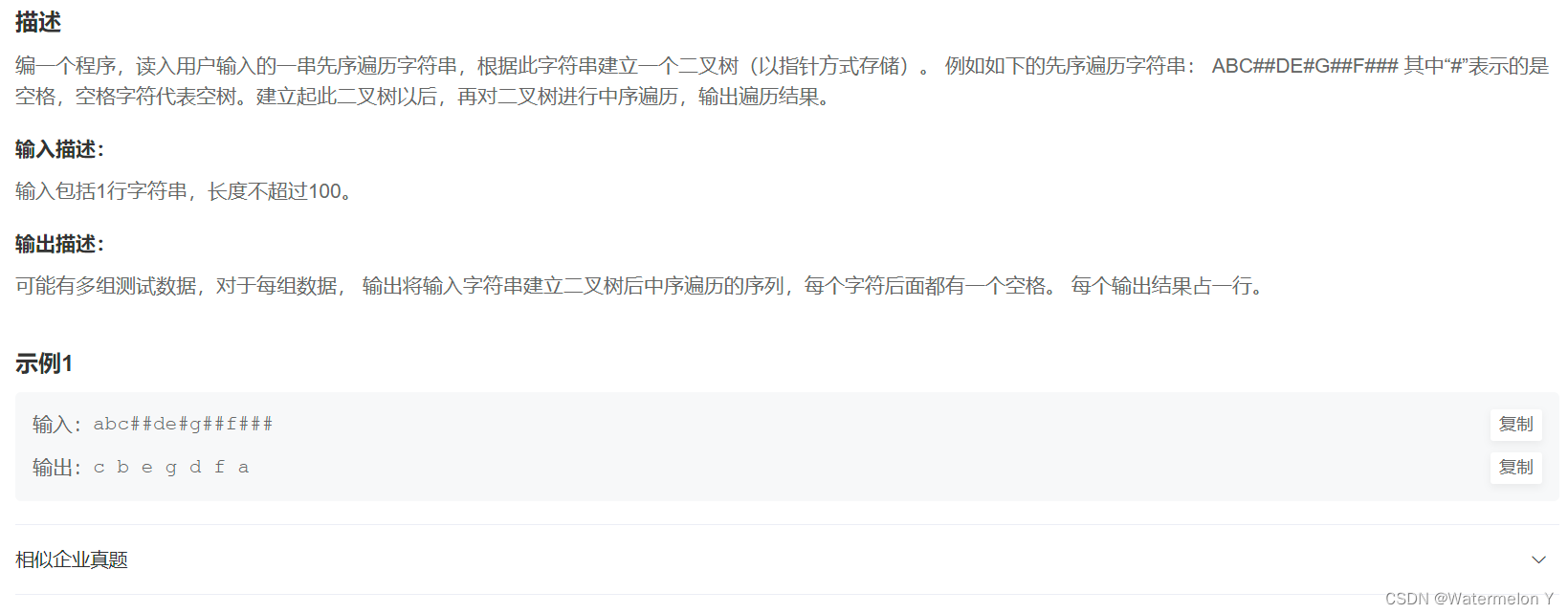
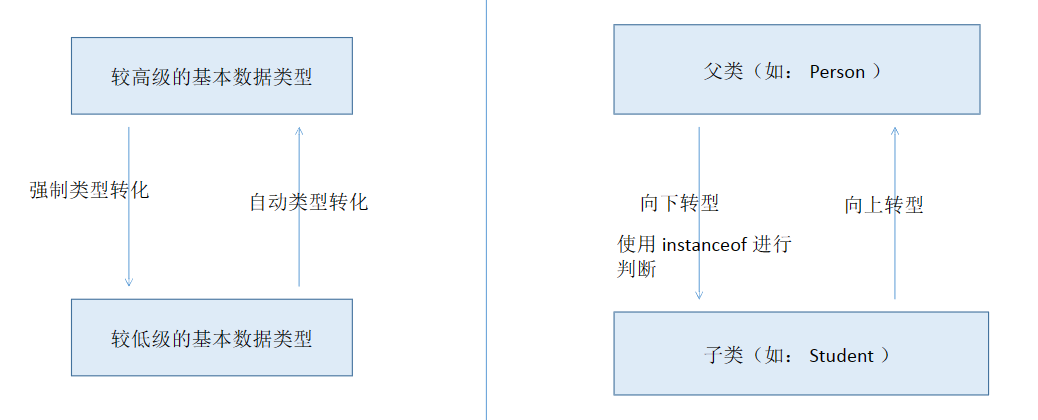
门把手行业分类

资料来源:共研产业咨询(共研网)
随着消费者对个性化需求的增加,门把手开始注重设计和创新。现代门把手的设计风格多样,涵盖了简约、欧式、中式等各种风格,并使用多种材质如金属、塑料、玻璃等,其中2022年中国门把手产量同比增长7.6%;销量同比增长10.4%。
2018-2022年中国门把手产量及销量

资料来源:共研产业咨询(共研网)
2023-2029年中国门把手市场深度调查与投资前景分析报告中显示:随着环保意识的提高,消费者对环保材料和工艺的要求也在增加;通过加强质量监管、推动创新设计和环保生产,门把手行业有望实现更好的发展。同时,个性化需求的增加和智能化趋势的兴起也将为门把手行业带来新的机遇,其中2022年中国门把手市场规模同比增长10%。
2018-2023年中国门把手市场规模及增速

资料来源:共研产业咨询(共研网)